Teorema Binomial: Desvio Padrão, Termos e Propriedades Relacionadas

O teorema binomial é uma das equações mais utilizadas no campo da matemática e também possui um grande número de aplicações em vários outros campos. Algumas das aplicações do mundo real do teorema binomial incluem:

• A distribuição de endereços IP para os computadores.
• Previsão de vários fatores relacionados à economia da nação.
• Previsão do tempo.
• Arquitetura.

O teorema binomial, também conhecido como expansão binomial, é usado em estatística, álgebra, probabilidade e vários outros campos da matemática e da física. O teorema binomial é denotado pela fórmula abaixo:

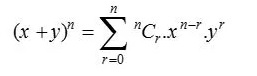
onde, n N e x,y R

Fonte

O que é um experimento binomial?

A fórmula do teorema binomial é geralmente usada para calcular a probabilidade do resultado de um experimento binomial. Um experimento binomial é um evento que pode ter apenas dois resultados. Por exemplo, prever chuva em um determinado dia; o resultado só pode ser um dos dois casos – ou vai chover naquele dia, ou não vai chover naquele dia.

Como existem apenas dois resultados fixos para uma situação, ela é chamada de experimento binomial. Você pode encontrar muitos exemplos de experimentos binomiais em sua vida diária. Jogar uma moeda, ganhar uma corrida, etc. são experimentos binomiais.

Leia: Distribuição binomial em Python com exemplos do mundo real

O que é uma distribuição binomial?

A distribuição binomial pode ser denominada para medir a probabilidade de algo acontecer ou não acontecer em um experimento binomial. Geralmente é representado como:

p: A probabilidade de um determinado resultado acontecer

n: O número de vezes que realizamos o experimento

Aqui estão alguns exemplos para ajudá-lo a entender,

• Se jogarmos os dados 10 vezes, então n = 10 ep para 1,2,3,4,5 e 6 será ⅙.
• Se lançarmos uma moeda 15 vezes, então n = 15 e p para cara e coroa será 1/2.

Existem muitos termos relacionados à distribuição binomial, que podem ajudá-lo a encontrar informações valiosas sobre qualquer problema. Vejamos os dois termos principais, desvio padrão e média da distribuição binomial.

Aprenda cursos de ciência de dados das melhores universidades do mundo. Ganhe Programas PG Executivos, Programas de Certificado Avançado ou Programas de Mestrado para acelerar sua carreira.

Desvio padrão de uma distribuição binomial

O desvio padrão de uma distribuição binomial é determinado pela fórmula abaixo:

= npq

Onde,

n = Número de tentativas

p = A probabilidade de tentativa bem sucedida

q = 1-p = A probabilidade de uma tentativa fracassada

Média de uma distribuição binomial

A média de uma distribuição binomial é determinada por,

= n*p

Onde,

n = Número de tentativas

p = A probabilidade de tentativa bem sucedida

Introdução ao teorema binomial

O teorema binomial pode ser visto como um método para expandir uma expressão de potência finita. Há algumas coisas que você precisa ter em mente sobre uma expansão binomial:

• Para uma equação (x+y)n o número de termos nesta expansão é n+1.
• Na expansão binomial, a soma dos expoentes de ambos os termos é n.
• C0n, C1n, C2n, …. é chamado de coeficientes binomiais.
• Os coeficientes binomiais que estão a uma distância igual do início e do fim são sempre iguais.

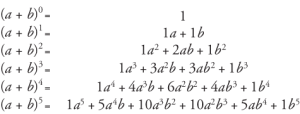
Fonte

Coeficientes de todos os termos podem ser encontrados olhando para o Triângulo de Pascal.

Fonte

Termos relacionados ao teorema binomial

Vejamos agora os termos mais usados ​​com o teorema binomial .

Termo geral

O termo geral no teorema binomial pode ser referido como uma equação genérica para qualquer termo dado, que corresponderá a esse termo específico se inserirmos os valores necessários nessa equação. Geralmente é representado como Tr+1.

Tr+1=Crn. xn-r. ano

Meio termo

O termo médio do teorema binomial pode ser referido como o valor do termo médio na expansão do teorema binomial.

Se o número de termos na expansão for par, o (n/2 + 1)º termo é o termo do meio, e se o número de termos na expansão binomial for ímpar, então [(n+1)/2]º e [(n+3)/2)ésimo são os termos médios.

Termo Independente

O termo que é independente das variáveis ​​na expansão de uma expressão é chamado de termo independente. O termo independente na expansão de axp + (b/xq)]n é

Tr+1 = nCr an-r br, onde r = (np/p+q), que é um número inteiro.

Propriedades do Teorema Binomial

1. C0 + C1 + C2 + … + Cn = 2n
2. C0 + C2 + C4 + … = C1 + C3 + C5 + … = 2n-1
3. C0 – C1 + C2 – C3 + … +(−1)n . nCn = 0
4. nC1 + 2.nC2 + 3.nC3 + … + n.nCn = n.2n-1
5. C1 − 2C2 + 3C3 − 4C4 + … +(−1)n-1 Cn = 0 para n > 1
6. C02 + C12 + C22 + …Cn2 = [(2n)!/ (n!)2]

Conclusão

O teorema binomial é uma das fórmulas mais usadas na matemática. Ele tem um dos usos mais importantes em estatística, que é usado para resolver problemas em ciência de dados.

Confira os cursos oferecidos pelo upGrad em parceria com as melhores universidades e líderes do setor. Alguns dos cursos oferecidos pelo upGrad são:

PG Diploma in Data Science : Este é um curso de 12 meses em Data Science fornecido pelo upGrad em associação com o IIIT-B.

Masters of Science in Data Science : Um curso de 18 meses fornecido pela upGrad em associação com o IIIT-B e a Liverpool John Moores University.

Certificação PG em Data Science : Um curso de 7 meses em Data Science fornecido pelo upGrad em associação com o IIIT-B.

Programa de Certificação de Business Analytics : Um curso introdutório de 3 meses em Data Science e Business Analytics fornecido pelo upGrad, é um dos melhores cursos de nível básico neste campo.