Teorema binomială: abaterea standard, termeni și proprietăți corelați

Teorema binomială este una dintre cele mai frecvent utilizate ecuații în domeniul matematicii și are, de asemenea, un număr mare de aplicații în diverse alte domenii. Unele dintre aplicațiile din lumea reală ale teoremei binomiale includ:

• Distribuirea adreselor IP către computere.
• Predicția diferiților factori legați de economia națiunii.
• Prognoza Meteo.
• Arhitectură.

Teorema binomială, cunoscută și sub denumirea de expansiune binomială, este folosită în statistică, algebră, probabilitate și în diverse alte domenii ale matematicii și fizicii. Teorema binomială se notează prin formula de mai jos:

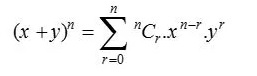
unde, n N și x,y R

Sursă

Ce este un experiment binom?

Formula teoremei binomiale este utilizată în general pentru calcularea probabilității rezultatului unui experiment binom. Un experiment binom este un eveniment care poate avea doar două rezultate. De exemplu, prezicerea ploii într-o anumită zi; rezultatul poate fi doar unul dintre cele două cazuri – fie va ploua în ziua respectivă, fie nu va ploua în acea zi.

Deoarece există doar două rezultate fixe pentru o situație, se numește experiment binom. Puteți găsi o mulțime de exemple de experimente binomiale în viața de zi cu zi. Aruncarea unei monede, câștigarea unei curse etc. sunt experimente binomiale.

Citiți: Distribuție binomială în Python cu exemple din lumea reală

Ce este o distribuție binomială?

Distribuția binomială poate fi numită pentru a măsura probabilitatea ca ceva să se întâmple sau să nu se întâmple într-un experiment binom. În general este reprezentat ca:

p: Probabilitatea ca un anumit rezultat să se întâmple

n: De câte ori efectuăm experimentul

Iată câteva exemple pentru a vă ajuta să înțelegeți,

• Dacă aruncăm zarurile de 10 ori, atunci n = 10 și p pentru 1,2,3,4,5 și 6 va fi ⅙.
• Dacă aruncăm o monedă de 15 ori, atunci n = 15 și p pentru cap și cozi va fi 1/2.

Există o mulțime de termeni legați de distribuția binomială, care vă pot ajuta să găsiți informații valoroase despre orice problemă. Să ne uităm la cei doi termeni principali, abaterea standard și media distribuției binomiale.

Învață cursuri de știință a datelor de la cele mai bune universități din lume. Câștigă programe Executive PG, programe avansate de certificat sau programe de master pentru a-ți accelera cariera.

Abaterea standard a unei distribuții binomiale

Abaterea standard a unei distribuții binomiale este determinată de formula de mai jos:

= npq

Unde,

n = Numărul de încercări

p = Probabilitatea de succes a procesului

q = 1-p = Probabilitatea unui proces eșuat

Media unei distribuții binomiale

Media unei distribuții binomiale este determinată de,

= n*p

Unde,

n = Numărul de încercări

p = Probabilitatea de succes a procesului

Introducere în teorema binomului

Teorema binomială poate fi văzută ca o metodă de extindere a expresiei unei puteri finite. Există câteva lucruri de care trebuie să ții cont despre o expansiune binomială:

• Pentru o ecuație (x+y)n numărul de termeni din această expansiune este n+1.
• În expansiunea binomială, suma exponenților ambilor termeni este n.
• C0n, C1n, C2n, …. se numește coeficienți binomi.
• Coeficienții binomi care sunt la o distanță egală de început și sfârșit sunt întotdeauna egali.

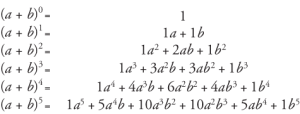
Sursă

Coeficienții tuturor termenilor pot fi găsiți uitându-se la Triunghiul lui Pascal.

Sursă

Termeni legați de teorema binomială

Să ne uităm acum la termenii cei mai des utilizați cu teorema binomială .

Termen general

Termenul general din teorema binomială poate fi menționat ca o ecuație generică pentru orice termen dat, care va corespunde acelui termen specific dacă inserăm valorile necesare în ecuația respectivă. Este de obicei reprezentat ca Tr+1.

Tr+1=Crn . xn-r . an

Termen mediu

Termenul mijlociu al teoremei binomului poate fi denumit valoarea termenului mijlociu în extinderea teoremei binomului.

Dacă numărul de termeni din expansiunea este par, (n/2 + 1) al-lea termen este termenul mijlociu, iar dacă numărul de termeni din expansiunea binomială este impar, atunci [(n+1)/2]-lea și [(n+3)/2)th sunt termenii mijlocii.

Termen independent

Termenul care este independent de variabilele în extinderea unei expresii se numește termen independent. Termenul independent în expansiunea axp + (b/xq)]n este

Tr+1 = nCr an-r br, unde r = (np/p+q) , care este un întreg.

Proprietățile teoremei binomiale

1. C0 + C1 + C2 + … + Cn = 2n
2. C0 + C2 + C4 + … = C1 + C3 + C5 + … = 2n-1
3. C0 – C1 + C2 – C3 + … +(−1)n . nCn = 0
4. nC1 + 2.nC2 + 3.nC3 + … + n.nCn = n.2n-1
5. C1 − 2C2 + 3C3 − 4C4 + … +(−1)n-1 Cn = 0 pentru n > 1
6. C02 + C12 + C22 + …Cn2 = [(2n)!/ (n!)2]

Concluzie

Teorema binomială este una dintre cele mai utilizate formule folosite în matematică. Are una dintre cele mai importante utilizări în statistică, care este folosită pentru a rezolva probleme în știința datelor.

Consultați cursurile oferite de upGrad în asociere cu universități de top și lideri din industrie. Unele dintre cursurile oferite de upGrad sunt:

Diploma PG în știința datelor : Acesta este un curs de 12 luni despre știința datelor oferit de upGrad în asociere cu IIIT-B.

Master în știința datelor : un curs de 18 luni oferit de upGrad în asociere cu IIIT-B și Liverpool John Moores University.

Certificare PG în știința datelor : un curs de 7 luni de știință a datelor oferit de upGrad în asociere cu IIIT-B.

Programul de certificare Business Analytics : Un curs introductiv de 3 luni despre Data Science și Business Analytics oferit de upGrad, este unul dintre cele mai bune cursuri de nivel de intrare în acest domeniu.