二项式定理：标准差、相关术语和性质

二项式定理是数学领域最常用的方程之一，在其他各个领域也有大量的应用。 二项式定理的一些实际应用包括：

• 将 IP 地址分配给计算机。
• 预测与国家经济有关的各种因素。
• 天气预报。
• 建筑学。

二项式定理，有时也称为二项式展开，用于统计、代数、概率以及其他各种数学和物理领域。 二项式定理由以下公式表示：

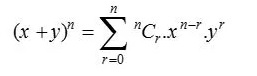
其中，n N 和 x,y R

资源

什么是二项式实验？

二项式定理公式通常用于计算二项式实验结果的概率。 二项式实验是一个只能有两个结果的事件。 例如，预测某一天的降雨； 结果只能是两种情况之一——要么那天下雨，要么那天不下雨。

由于一种情况只有两个固定结果，因此称为二项式实验。 你可以在日常生活中找到很多二项式实验的例子。 抛硬币、赢得比赛等都是二项式实验。

阅读： Python 中的二项式分布与实际示例

什么是二项分布？

二项分布可以被称为衡量在二项式实验中某事发生或不发生的概率。 一般表示为：

p：特定结果发生的概率

n：我们进行实验的次数

这里有一些例子可以帮助你理解，

• 如果我们掷骰子 10 次，那么 n = 10 和 p 为 1,2,3,4,5 和 6 将是 ⅙。
• 如果我们抛硬币 15 次，那么 n = 15，正面和反面的 p 将是 1/2。

有很多与二项分布相关的术语，可以帮助您找到有关任何问题的有价值的见解。 让我们看一下二项分布的两个主要术语，标准差和均值。

学习世界顶尖大学的数据科学课程。 获得行政 PG 课程、高级证书课程或硕士课程，以加快您的职业生涯。

二项分布的标准差

二项分布的标准差由以下公式确定：

= npq

在哪里，

n = 试验次数

p = 成功试验的概率

q = 1-p = 试验失败的概率

二项分布的平均值

二项分布的均值由下式确定，

= n*p

在哪里，

n = 试验次数

p = 成功试验的概率

二项式定理简介

二项式定理可以看作是一种扩展有限幂表达式的方法。 关于二项式展开，您需要记住以下几点：

• 对于方程 (x+y)n，此展开式中的项数为 n+1。
• 在二项式展开中，两项的指数之和为 n。
• C0n，C1n，C2n，……。 称为二项式系数。
• 与起点和终点距离相等的二项式系数总是相等的。

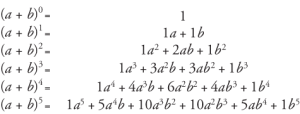
资源

通过查看帕斯卡三角可以找到所有项的系数。

资源

与二项式定理相关的术语

现在让我们看看二项式定理中最常用的术语。

一般术语

二项式定理中的一般项可以称为任何给定项的通用方程，如果我们在该方程中插入必要的值，它将对应于该特定项。 它通常表示为 Tr+1。

Tr+1=Crn 。 xn-r 。 年

中期

二项式定理的中项可以称为二项式定理扩展中的中项值。

如果展开式中的项数为偶数，则第(n/2 + 1)项为中项，若二项式展开式中的项数为奇数，则第[(n+1)/2]项和 [(n+3)/2)th 是中间项。

独立任期

在表达式的展开中与变量无关的项称为独立项。 axp + (b/xq)]n 展开式中的独立项是

Tr+1 = nCr an-r br，其中 r = (np/p+q) ，它是一个整数。

二项式定理的性质

1. C0 + C1 + C2 + … + Cn = 2n
2. C0 + C2 + C4 + … = C1 + C3 + C5 + … = 2n-1
3. C0 – C1 + C2 – C3 + … +(−1)n 。 nCn = 0
4. nC1 + 2.nC2 + 3.nC3 + … + n.nCn = n.2n-1
5. C1 - 2C2 + 3C3 - 4C4 + … +(-1)n-1 Cn = 0，n > 1
6. C02 + C12 + C22 + …Cn2 = [(2n)!/ (n!)2]

结论

二项式定理是数学中最常用的公式之一。 它在统计学中具有最重要的用途之一，用于解决数据科学中的问题。

查看upGrad与顶尖大学和行业领导者联合提供的课程。 upGrad 提供的一些课程包括：

PG 数据科学文凭：这是由 upGrad 与 IIIT-B 联合提供的为期 12 个月的数据科学课程。

数据科学理学硕士：由 upGrad 与 IIIT-B 和利物浦约翰摩尔斯大学联合提供的为期 18 个月的课程。

数据科学 PG 认证：由 upGrad 与 IIIT-B 联合提供的为期 7 个月的数据科学课程。

商业分析认证计划：由 upGrad 提供的为期 3 个月的数据科学和商业分析入门课程，是该领域最好的入门级课程之一。