Teorema binomiale: deviazione standard, termini e proprietà correlati

Il teorema binomiale è una delle equazioni più utilizzate nel campo della matematica e ha anche un gran numero di applicazioni in vari altri campi. Alcune delle applicazioni nel mondo reale del teorema binomiale includono:

• La distribuzione di indirizzi IP ai computer.
• Previsione di vari fattori legati all'economia della nazione.
• Previsioni del tempo.
• Architettura.

Il teorema binomiale, noto anche come espansione binomiale, è utilizzato in statistica, algebra, probabilità e vari altri campi della matematica e della fisica. Il teorema binomiale è indicato dalla formula seguente:

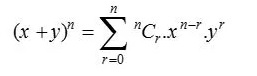
dove, n N e x,y R

Fonte

Che cos'è un esperimento binomiale?

La formula del teorema binomiale viene generalmente utilizzata per calcolare la probabilità del risultato di un esperimento binomiale. Un esperimento binomiale è un evento che può avere solo due risultati. Ad esempio, prevedere la pioggia in un giorno particolare; il risultato può essere solo uno dei due casi: o pioverà quel giorno, o quel giorno non pioverà.

Poiché ci sono solo due risultati fissi in una situazione, si parla di esperimento binomiale. Puoi trovare molti esempi di esperimenti binomiali nella tua vita quotidiana. Lanciare una moneta, vincere una gara, ecc. sono esperimenti binomiali.

Leggi: Distribuzione binomiale in Python con esempi del mondo reale

Che cos'è una distribuzione binomiale?

La distribuzione binomiale può essere definita per misurare la probabilità che qualcosa accada o non accada in un esperimento binomiale. Viene generalmente rappresentato come:

p: La probabilità che si verifichi un determinato risultato

n: Il numero di volte in cui eseguiamo l'esperimento

Ecco alcuni esempi per aiutarti a capire,

• Se lanciamo i dadi 10 volte, allora n = 10 e p per 1,2,3,4,5 e 6 sarà ⅙.
• Se lanciamo una moneta per 15 volte, allora n = 15 e p per testa e croce sarà 1/2.

Esistono molti termini relativi alla distribuzione binomiale, che possono aiutarti a trovare preziose informazioni su qualsiasi problema. Diamo un'occhiata ai due termini principali, deviazione standard e media della distribuzione binomiale.

Impara i corsi di scienza dei dati dalle migliori università del mondo. Guadagna programmi Executive PG, programmi di certificazione avanzati o programmi di master per accelerare la tua carriera.

Deviazione standard di una distribuzione binomiale

La deviazione standard di una distribuzione binomiale è determinata dalla formula seguente:

= npq

Dove,

n = Numero di prove

p = La probabilità di successo della prova

q = 1-p = La probabilità di un tentativo fallito

Media di una distribuzione binomiale

La media di una distribuzione binomiale è determinata da

= n*p

Dove,

n = Numero di prove

p = La probabilità di successo della prova

Introduzione al teorema binomiale

Il teorema binomiale può essere visto come un metodo per espandere un'espressione di potenza finita. Ci sono alcune cose che devi tenere a mente su un'espansione binomiale:

• Per un'equazione (x+y)n il numero di termini in questa espansione è n+1.
• Nell'espansione binomiale, la somma degli esponenti di entrambi i termini è n.
• C0n, C1n, C2n, …. prende il nome di coefficienti binomiali.
• I coefficienti binomiali che sono alla stessa distanza dall'inizio e dalla fine sono sempre uguali.

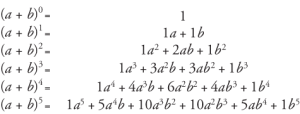
Fonte

I coefficienti di tutti i termini possono essere trovati osservando il Triangolo di Pascal.

Fonte

Termini relativi al teorema binomiale

Vediamo ora i termini più usati con il teorema del binomio .

Termine generale

Il termine generale nel teorema binomiale può essere indicato come un'equazione generica per un dato termine, che corrisponderà a quel termine specifico se inseriamo i valori necessari in quell'equazione. Di solito è rappresentato come Tr+1.

Tr+1=Crn . xn-r . anno

Medio termine

Il termine medio del teorema binomiale può essere indicato come valore del termine medio nell'espansione del teorema binomiale.

Se il numero di termini nell'espansione è pari, il (n/2 + 1)esimo termine è il termine medio, e se il numero di termini nell'espansione binomiale è dispari, allora [(n+1)/2]esimo e [(n+3)/2)esimo sono i termini medi.

Termine indipendente

Il termine che è indipendente dalle variabili nell'espansione di un'espressione è chiamato termine indipendente. Il termine indipendente nell'espansione di axp + (b/xq)]n è

Tr+1 = nCr an-r br, dove r = (np/p+q) , che è un numero intero.

Proprietà del teorema binomiale

1. C0 + C1 + C2 + … + Cn = 2n
2. C0 + C2 + C4 + … = C1 + C3 + C5 + … = 2n-1
3. C0 – C1 + C2 – C3 + … +(−1)n . nCn = 0
4. nC1 + 2.nC2 + 3.nC3 + … + n.nCn = n.2n-1
5. C1 − 2C2 + 3C3 − 4C4 + … +(−1)n-1 Cn = 0 per n > 1
6. C02 + C12 + C22 + …Cn2 = [(2n)!/ (n!)2]

Conclusione

Il teorema binomiale è una delle formule più utilizzate in matematica. Ha uno degli usi più importanti nella statistica, che viene utilizzato per risolvere i problemi nella scienza dei dati.

Scopri i corsi offerti da upGrad in collaborazione con le migliori università e leader del settore. Alcuni dei corsi offerti da upGrad sono:

Diploma PG in Data Science : questo è un corso di 12 mesi su Data Science fornito da upGrad in associazione con IIIT-B.

Master in Data Science : un corso di 18 mesi fornito da upGrad in associazione con IIIT-B e Liverpool John Moores University.

Certificazione PG in Data Science : un corso di 7 mesi su Data Science fornito da upGrad in associazione con IIIT-B.

Programma di certificazione di Business Analytics : un corso introduttivo di 3 mesi su Data Science e Business Analytics fornito da upGrad, è uno dei migliori corsi di livello base in questo campo.