Théorème binomial : écart type, termes et propriétés connexes

Le théorème binomial est l'une des équations les plus fréquemment utilisées dans le domaine des mathématiques et a également un grand nombre d'applications dans divers autres domaines. Certaines des applications réelles du théorème binomial incluent:

• La distribution des adresses IP aux ordinateurs.
• Prédiction de divers facteurs liés à l'économie de la nation.
• Prévision météo.
• Architecture.

Le théorème binomial, également parfois appelé développement binomial, est utilisé en statistique, en algèbre, en probabilité et dans divers autres domaines des mathématiques et de la physique. Le théorème du binôme est noté par la formule ci-dessous :

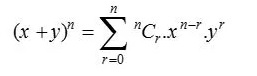
où, n N et x,y R

La source

Qu'est-ce qu'une expérience binomiale ?

La formule du théorème binomial est généralement utilisée pour calculer la probabilité du résultat d'une expérience binomiale. Une expérience binomiale est un événement qui ne peut avoir que deux résultats. Par exemple, prédire la pluie un jour particulier ; le résultat ne peut être que l'un des deux cas - soit il pleuvra ce jour-là, soit il ne pleuvra pas ce jour-là.

Puisqu'il n'y a que deux résultats fixes dans une situation, on parle d'expérience binomiale. Vous pouvez trouver de nombreux exemples d'expériences binomiales dans votre vie quotidienne. Lancer une pièce de monnaie, gagner une course, etc. sont des expériences binomiales.

Lire : Distribution binomiale en Python avec des exemples réels

Qu'est-ce qu'une distribution binomiale ?

La distribution binomiale peut être appelée pour mesurer la probabilité que quelque chose se produise ou ne se produise pas dans une expérience binomiale. Il est généralement représenté par :

p : La probabilité qu'un résultat particulier se produise

n : Le nombre de fois que nous réalisons l'expérience

Voici quelques exemples pour vous aider à comprendre,

• Si nous lançons les dés 10 fois, alors n = 10 et p pour 1,2,3,4,5 et 6 sera ⅙.
• Si nous lançons une pièce 15 fois, alors n = 15 et p pour pile et face sera 1/2.

Il existe de nombreux termes liés à la distribution binomiale, qui peuvent vous aider à trouver des informations précieuses sur n'importe quel problème. Regardons les deux termes principaux, écart-type et moyenne de la distribution binomiale.

Apprenez des cours de science des données dans les meilleures universités du monde. Gagnez des programmes Executive PG, des programmes de certificat avancés ou des programmes de maîtrise pour accélérer votre carrière.

Écart type d'une distribution binomiale

L'écart type d'une distribution binomiale est déterminé par la formule ci-dessous :

= npq

Où,

n = nombre d'essais

p = La probabilité d'un essai réussi

q = 1-p = La probabilité d'échec d'un essai

Moyenne d'une distribution binomiale

La moyenne d'une distribution binomiale est déterminée par,

= n*p

Où,

n = nombre d'essais

p = La probabilité d'un essai réussi

Introduction au théorème du binôme

Le théorème binomial peut être vu comme une méthode pour développer une expression de puissance finie. Il y a quelques choses que vous devez garder à l'esprit à propos d'une expansion binomiale :

• Pour une équation (x+y)n le nombre de termes dans ce développement est n+1.
• Dans le développement binomial, la somme des exposants des deux termes est n.
• C0n, C1n, C2n, …. s'appelle les coefficients binomiaux.
• Les coefficients binomiaux qui sont à égale distance du début et de la fin sont toujours égaux.

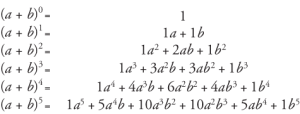
La source

Les coefficients de tous les termes peuvent être trouvés en regardant le triangle de Pascal.

La source

Termes liés au théorème du binôme

Voyons maintenant les termes les plus fréquemment utilisés avec le théorème du binôme .

Terme général

Le terme général dans le théorème binomial peut être appelé une équation générique pour tout terme donné, qui correspondra à ce terme spécifique si nous insérons les valeurs nécessaires dans cette équation. Il est généralement représenté par Tr+1.

Tr+1=Crn . xn-r . an

Moyen terme

Le terme moyen du théorème binomial peut être appelé la valeur du terme moyen dans le développement du théorème binomial.

Si le nombre de termes dans le développement est pair, le (n/2 + 1)ème terme est le terme moyen, et si le nombre de termes dans le développement binomial est impair, alors [(n+1)/2]ème et [(n+3)/2)th sont les termes moyens.

Mandat indépendant

Le terme qui est indépendant des variables dans le développement d'une expression est appelé le terme indépendant. Le terme indépendant dans le développement de axp + (b/xq)]n est

Tr+1 = nCr an-r br, où r = (np/p+q) , qui est un entier.

Propriétés du théorème binomial

1. C0 + C1 + C2 + … + Cn = 2n
2. C0 + C2 + C4 + … = C1 + C3 + C5 + … = 2n-1
3. C0 – C1 + C2 – C3 + … +(−1)n . nCn = 0
4. nC1 + 2.nC2 + 3.nC3 + … + n.nCn = n.2n-1
5. C1 − 2C2 + 3C3 − 4C4 + … +(−1)n-1 Cn = 0 pour n > 1
6. C02 + C12 + C22 + …Cn2 = [(2n)!/ (n!)2]

Conclusion

Le théorème binomial est l'une des formules les plus utilisées en mathématiques. Il a l'une des utilisations les plus importantes en statistique, qui est utilisée pour résoudre des problèmes en science des données.

Découvrez les cours dispensés par upGrad en association avec les meilleures universités et les leaders de l'industrie. Certains des cours offerts par upGrad sont:

Diplôme PG en science des données : Il s'agit d'un cours de 12 mois sur la science des données dispensé par upGrad en association avec l'IIIT-B.

Master of Science in Data Science : Un cours de 18 mois dispensé par upGrad en association avec IIIT-B et Liverpool John Moores University.

Certification PG en Data Science : Un cours de 7 mois sur la Data Science dispensé par upGrad en association avec l'IIIT-B.

Programme de certification Business Analytics : Un cours d'introduction de 3 mois sur la science des données et l'analyse commerciale fourni par upGrad, est l'un des meilleurs cours d'entrée de gamme dans ce domaine.