Teorema del binomio: desviación estándar, términos y propiedades relacionados
Publicado: 2020-09-28El teorema del binomio es una de las ecuaciones más utilizadas en el campo de las matemáticas y también tiene una gran cantidad de aplicaciones en varios otros campos. Algunas de las aplicaciones del mundo real del teorema del binomio incluyen:
- La distribución de direcciones IP a las computadoras.
- Predicción de diversos factores relacionados con la economía de la nación.
- Predicción del tiempo.
- Arquitectura.
El teorema binomial, también conocido a veces como expansión binomial, se usa en estadística, álgebra, probabilidad y otros campos de las matemáticas y la física. El teorema del binomio se denota mediante la siguiente fórmula:
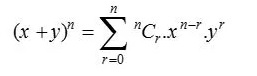
donde, n N y x,y R
Fuente
Tabla de contenido
¿Qué es un experimento binomial?
La fórmula del teorema binomial generalmente se usa para calcular la probabilidad del resultado de un experimento binomial. Un experimento binomial es un evento que solo puede tener dos resultados. Por ejemplo, predecir la lluvia en un día en particular; el resultado solo puede ser uno de los dos casos: lloverá ese día o no lloverá ese día.
Dado que solo hay dos resultados fijos en una situación, se denomina experimento binomial. Puedes encontrar muchos ejemplos de experimentos binomiales en tu vida diaria. Tirar una moneda, ganar una carrera, etc. son experimentos binomiales.
Leer: Distribución binomial en Python con ejemplos del mundo real
¿Qué es una distribución binomial?
La distribución binomial se puede denominar para medir la probabilidad de que algo suceda o no suceda en un experimento binomial. Generalmente se representa como:
p: La probabilidad de que ocurra un resultado particular
n: El número de veces que realizamos el experimento
Aquí hay algunos ejemplos para ayudarlo a entender,
- Si lanzamos los dados 10 veces, entonces n = 10 y p para 1,2,3,4,5 y 6 será ⅙.
- Si lanzamos una moneda 15 veces, entonces n = 15 y p para cara y cruz será 1/2.
Hay muchos términos relacionados con la distribución binomial, que pueden ayudarlo a encontrar información valiosa sobre cualquier problema. Veamos los dos términos principales, la desviación estándar y la media de la distribución binomial.
Aprenda cursos de ciencia de datos de las mejores universidades del mundo. Obtenga programas Executive PG, programas de certificados avanzados o programas de maestría para acelerar su carrera.
Desviación estándar de una distribución binomial
La desviación estándar de una distribución binomial está determinada por la siguiente fórmula:
= npq
Donde,
n = Número de ensayos
p = La probabilidad de prueba exitosa
q = 1-p = La probabilidad de una prueba fallida
Media de una distribución binomial
La media de una distribución binomial está determinada por,
= n*p
Donde,
n = Número de ensayos
p = La probabilidad de prueba exitosa
Introducción al teorema del binomio
El teorema del binomio puede verse como un método para expandir una expresión de potencia finita. Hay algunas cosas que debe tener en cuenta acerca de una expansión binomial:
- Para una ecuación (x+y)n, el número de términos en esta expansión es n+1.
- En la expansión binomial, la suma de los exponentes de ambos términos es n.
- C0n, C1n, C2n, …. se llama los coeficientes binomiales.
- Los coeficientes binomiales que están a la misma distancia del principio y del final son siempre iguales.
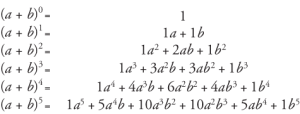

Fuente
Los coeficientes de todos los términos se pueden encontrar observando el Triángulo de Pascal.
Fuente
Términos relacionados con el teorema del binomio
Veamos ahora los términos más utilizados con el teorema del binomio .
Termino general
El término general en el teorema del binomio puede denominarse ecuación genérica para cualquier término dado, que corresponderá a ese término específico si insertamos los valores necesarios en esa ecuación. Suele representarse como Tr+1.
Tr+1=Crn. xn-r. año
Termino medio
El término medio del teorema del binomio se puede denominar como el valor del término medio en la expansión del teorema del binomio.
Si el número de términos en la expansión es par, el (n/2 + 1)-ésimo término es el término del medio, y si el número de términos en la expansión binomial es impar, entonces [(n+1)/2]-ésimo y [(n+3)/2)th son los términos medios.
Término Independiente
El término que es independiente de las variables en la expansión de una expresión se llama término independiente. El término independiente en el desarrollo de axp + (b/xq)]n es
Tr+1 = nCr an-r br, donde r = (np/p+q), que es un número entero.
Propiedades del teorema del binomio
- C0 + C1 + C2 + … + Cn = 2n
- C0 + C2 + C4 + … = C1 + C3 + C5 + … = 2n-1
- C0 – C1 + C2 – C3 + … +(−1)n . nCn = 0
- nC1 + 2.nC2 + 3.nC3 + … + n.nCn = n.2n-1
- C1 − 2C2 + 3C3 − 4C4 + … +(−1)n-1 Cn = 0 para n > 1
- C02 + C12 + C22 + …Cn2 = [(2n)!/ (n!)2]
Conclusión
El teorema del binomio es una de las fórmulas más utilizadas en matemáticas. Tiene uno de los usos más importantes en estadística, que se utiliza para resolver problemas en ciencia de datos.
Consulte los cursos proporcionados por upGrad en asociación con las mejores universidades y líderes de la industria. Algunos de los cursos que ofrece upGrad son:
Diploma PG en ciencia de datos : este es un curso de 12 meses en ciencia de datos proporcionado por upGrad en asociación con IIIT-B.
Maestría en Ciencias en Ciencia de Datos : un curso de 18 meses proporcionado por upGrad en asociación con IIIT-B y la Universidad John Moores de Liverpool.
Certificación PG en ciencia de datos : un curso de 7 meses sobre ciencia de datos proporcionado por upGrad en asociación con IIIT-B.
Programa de certificación de análisis empresarial : un curso introductorio de 3 meses sobre ciencia de datos y análisis empresarial proporcionado por upGrad, es uno de los mejores cursos de nivel de entrada en este campo.
En análisis estadístico y de probabilidad, a menudo se utiliza el teorema del binomio. Es bastante beneficioso, ya que nuestra economía depende en gran medida de los análisis estadísticos y de probabilidad. El teorema del binomio se usa en matemáticas avanzadas y computación para identificar raíces de ecuaciones en potencias superiores. También se usa para probar muchas ecuaciones clave de física y matemáticas. Los servicios de pronóstico del tiempo, la arquitectura y la estimación de costos en proyectos de ingeniería también utilizan el teorema del binomio. El triángulo de Pascal es una alternativa basada en diagramas a los enfoques algebraicos para calcular los coeficientes que surgen en las expansiones binomiales. Este puede ser un método simple para determinar los coeficientes de una expansión binomial con un exponente pequeño. La distribución binomial es una distribución de Bernoulli para un único ensayo, es decir, cuando el valor de n es 1. Un ensayo de Bernoulli o un experimento de Bernoulli es un único experimento de éxito/fracaso, mientras que un proceso binomial es una secuencia de resultados. El teorema de Bernoulli trata el resultado de una sola prueba de un evento, pero el teorema del binomio trata el resultado de varias pruebas del mismo evento. Cuando el resultado de un evento se requiere una sola vez, se emplea Bernoulli, pero se usa el binomio cuando el resultado se requiere varias veces.¿De qué manera entra en juego el teorema del binomio en la vida cotidiana?
¿Qué implica un Triángulo de Pascal?
¿Hay alguna diferencia entre binomial y Bernoulli?
