Teorema Binomial: Deviasi Standar, Syarat & Sifat Terkait

Teorema binomial adalah salah satu persamaan yang paling sering digunakan dalam bidang matematika dan juga memiliki banyak aplikasi di berbagai bidang lainnya. Beberapa aplikasi dunia nyata dari teorema binomial meliputi:

• Distribusi Alamat IP ke komputer.
• Prediksi berbagai faktor yang berkaitan dengan perekonomian bangsa.
• Perkiraan cuaca.
• Arsitektur.

Teorema binomial, juga kadang-kadang dikenal sebagai ekspansi binomial, digunakan dalam statistik, aljabar, probabilitas, dan berbagai bidang matematika dan fisika lainnya. Teorema binomial dilambangkan dengan rumus di bawah ini:

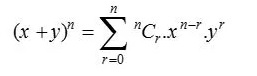
dimana, n N dan x,y R

Sumber

Apa itu Eksperimen Binomial?

Rumus teorema binomial umumnya digunakan untuk menghitung probabilitas hasil percobaan binomial. Eksperimen binomial adalah kejadian yang hanya memiliki dua hasil. Misalnya, memprediksi hujan pada hari tertentu; hasilnya hanya salah satu dari dua kasus – baik akan hujan pada hari itu, atau tidak hujan pada hari itu.

Karena hanya ada dua hasil tetap untuk suatu situasi, ini disebut sebagai eksperimen binomial. Anda dapat menemukan banyak contoh eksperimen binomial dalam kehidupan sehari-hari Anda. Melempar koin, memenangkan perlombaan, dll adalah eksperimen binomial.

Baca: Distribusi Binomial di Python dengan Contoh Dunia Nyata

Apa itu Distribusi Binomial?

Distribusi binomial dapat disebut untuk mengukur probabilitas sesuatu terjadi atau tidak terjadi dalam eksperimen binomial. Secara umum direpresentasikan sebagai:

p: Probabilitas bahwa hasil tertentu akan terjadi

n: Berapa kali kita melakukan eksperimen

Berikut adalah beberapa contoh untuk membantu Anda memahami,

• Jika kita melempar dadu 10 kali, maka n = 10 dan p untuk 1,2,3,4,5 dan 6 adalah .
• Jika kita melempar koin sebanyak 15 kali, maka n = 15 dan p untuk kepala dan ekor adalah 1/2.

Ada banyak istilah yang terkait dengan distribusi binomial, yang dapat membantu Anda menemukan wawasan berharga tentang masalah apa pun. Mari kita lihat dua istilah utama, standar deviasi dan mean dari distribusi binomial.

Pelajari kursus ilmu data dari Universitas top dunia. Dapatkan Program PG Eksekutif, Program Sertifikat Tingkat Lanjut, atau Program Magister untuk mempercepat karier Anda.

Simpangan baku dari distribusi binomial

Standar deviasi dari distribusi binomial ditentukan oleh rumus di bawah ini:

= npq

Di mana,

n = Jumlah percobaan

p = Probabilitas percobaan yang berhasil

q = 1-p = Probabilitas percobaan yang gagal

Rata-rata dari distribusi binomial

Mean dari distribusi binomial ditentukan oleh,

= n*p

Di mana,

n = Jumlah percobaan

p = Probabilitas percobaan yang berhasil

Pengantar teorema binomial

Teorema binomial dapat dilihat sebagai metode untuk memperluas ekspresi pangkat hingga. Ada beberapa hal yang perlu diingat tentang ekspansi binomial:

• Untuk persamaan (x+y)n jumlah suku dalam pemuaian ini adalah n+1.
• Dalam ekspansi binomial, jumlah eksponen kedua suku adalah n.
• C0n, C1n, C2n, …. disebut koefisien binomial.
• Koefisien binomial yang berada pada jarak yang sama dari awal dan akhir selalu sama.

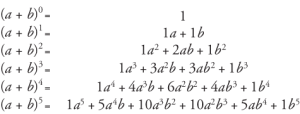
Sumber

Koefisien semua suku dapat ditemukan dengan melihat Segitiga Pascal.

Sumber

Istilah-istilah yang berkaitan dengan teorema binomial

Mari kita lihat istilah yang paling sering digunakan dengan teorema binomial .

Istilah Umum

Istilah umum dalam teorema binomial dapat disebut sebagai persamaan umum untuk setiap istilah tertentu, yang akan sesuai dengan istilah khusus itu jika kita memasukkan nilai yang diperlukan dalam persamaan itu. Biasanya direpresentasikan sebagai Tr+1.

Tr+1=Crn . xn-r . tahun

Istilah Tengah

Suku tengah teorema binomial dapat disebut sebagai nilai suku tengah dalam perluasan teorema binomial.

Jika jumlah suku pada pemuaian genap, suku ke (n/2 + 1) adalah suku tengah, dan jika jumlah suku pada pemuaian binomial ganjil, maka ke [(n+1)/2] dan [(n+3)/2)th adalah suku tengah.

Istilah Independen

Suku yang bebas dari variabel dalam perluasan suatu ekspresi disebut suku bebas. Suku bebas dalam perluasan axp + (b/xq)]n adalah

Tr+1 = nCr an-r br, di mana r = (np/p+q) , yang merupakan bilangan bulat.

Sifat-sifat Teorema Binomial

1. C0 + C1 + C2 + … + Cn = 2n
2. C0 + C2 + C4 + … = C1 + C3 + C5 + … = 2n-1
3. C0 – C1 + C2 – C3 + … +(−1)n . nCn = 0
4. nC1 + 2.nC2 + 3.nC3 + … + n.nCn = n.2n-1
5. C1 2C2 + 3C3 4C4 + … +(−1)n-1 Cn = 0 untuk n > 1
6. C02 + C12 + C22 + …Cn2 = [(2n)!/ (n!)2]

Kesimpulan

Teorema binomial adalah salah satu rumus yang paling sering digunakan dalam matematika. Ini memiliki salah satu kegunaan terpenting dalam statistik, yang digunakan untuk memecahkan masalah dalam ilmu data.

Lihat kursus yang disediakan oleh upGrad bekerja sama dengan universitas terkemuka dan pemimpin industri. Beberapa program studi yang ditawarkan oleh upGrad adalah:

Diploma PG dalam Ilmu Data : Ini adalah kursus 12 bulan tentang Ilmu Data yang disediakan oleh upGrad bekerja sama dengan IIIT-B.

Master of Science dalam Ilmu Data : Kursus 18 bulan yang disediakan oleh upGrad bekerja sama dengan IIIT-B dan Liverpool John Moores University.

Sertifikasi PG dalam Ilmu Data : Kursus selama 7 bulan tentang Ilmu Data yang disediakan oleh upGrad bekerja sama dengan IIIT-B.

Program Sertifikasi Analisis Bisnis : Kursus pengantar 3 bulan tentang Ilmu Data dan Analisis Bisnis yang disediakan oleh upGrad, adalah salah satu kursus tingkat pemula terbaik di bidang ini.