Граф сверточных сетей: список приложений, которые вам нужно знать

Сверточная сеть — это тип нейронной сети. Нейронные сети — это особый вид модели глубокого обучения. Как правило, машинное обучение или глубокое обучение включает в себя строгие и дорогие алгоритмы из-за сложной задачи. Точно так же модели глубокого обучения на графах еще сложнее. Графические сверточные сети в основном используются для классификации изображений. Узнайте больше о сверточной нейронной сети.

За последнее десятилетие применение науки о данных значительно возросло. В этом богатом данными мире подход с использованием модели обучения принес отличные результаты и точные прогнозы. Графики полезны для многих информационных систем.

От взаимодействия биологических белков до подключения к Интернету и WorldWideWeb — графы представляют все эти системы. Кроме того, реализация нейронных сетей через графическую структуру позволяет компьютеру понять свойства изображения. Эта модель является одним из самых передовых приложений графа в реальном мире. Рассмотрим эти алгоритмы подробно:

Как строятся нейронные сети

Нейронные сети — один из самых передовых методов науки о данных и глубокого обучения. Нейронные сети полезны во многих приложениях, от предсказания фондового рынка до классификации изображений, распознавания речи или символов и даже в анализе последовательности.

Первая концепция нейронной сети возникла с биологической точки зрения. Ученые проводили эксперименты, в которых зрительные нервы соединялись со слуховыми центрами головного мозга. Со временем организм научился видеть и через слуховой центр мозга. Дальнейшие эксперименты доказали, что каждый центр мозга может выполнять любое действие.

Подходы начали имитировать человеческий мозг, информируя компьютерные алгоритмы. Точно так же ученые-компьютерщики также думали, что должен быть единый алгоритм, способный решить все проблемы обучения компьютерного мозга. Так родилась нейронная сеть.

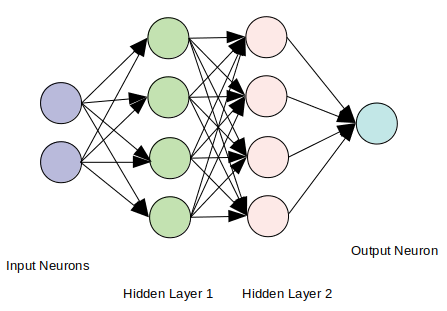
Нейронная сеть состоит из нескольких слоев нейронов. Каждый нейрон обычно является узлом графа. Каждый нейрон каждого слоя связан со всеми нейронами следующего слоя через взвешенное ребро — веса ребра выступают в роли коэффициента вычисления значения слоя.

Благодаря обратному распространению коэффициенты изменяются, чтобы соответствовать модели с примерами обучающих примеров. В конечном итоге выход дает один нейрон из последнего слоя. На следующем изображении объясняется структура нейронной сети.

Источник изображения

Читайте: Использование сверточной нейронной сети для классификации изображений

Граф сверточных сетей

Сверточные сети — это трехмерные нейронные сети. Большинство практических применений сверточных нейронных сетей включают классификацию и распознавание изображений, обработку естественного языка и распознавание речи. Эти модели обычно более сложны, чем обычные двумерные модели нейронных сетей.

В этой архитектуре собраны слои разных нейронов. Параметр размеров является переменным в разных слоях, чтобы модель распознавала параметры. Например, изображения двухмерны, а между тем цвет каждой точки также играет решающую роль. Таким образом, появляются три различных параметра. Чтобы справиться с такими сложностями, Conv Nets играют важную роль.

Эти многочисленные трехмерные матрицы разных размеров работают на нескольких уровнях нейронной сети. В конце концов, размерность «z» соответствует выходному параметру сети. Передача информации с одного уровня на другой может осуществляться с помощью различных алгоритмов.

Например, FC (Fully Connected), объединение в пул и ReLU являются важными алгоритмами в этом отношении.

Как правило, значения узлов нейронной сети обозначаются знаком , где «l» означает номер слоя. Итак, 0 - это входная матрица.

а 0 = Х

С другой стороны, последний узел слоя определяет вывод. Скажем, есть слои «L». Поэтому L обозначает выход нейронной сети.

а Л = Y

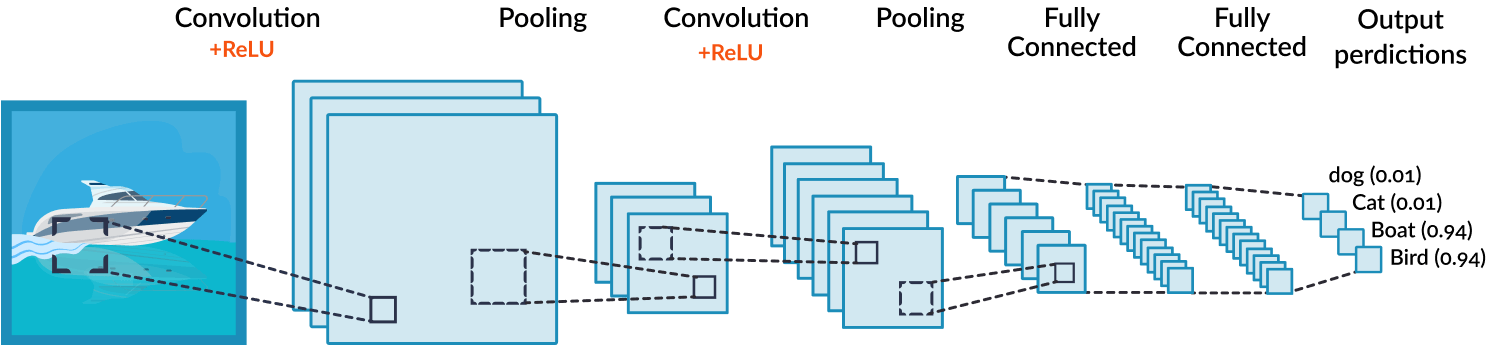
Источник изображения

На изображении выше изображена сверточная нейронная сеть при реализации классификации изображений. Параметры заданы для собаки, кошки, летучей мыши и птицы.

Значение узла определенного внутреннего слоя вычисляется на основе значений предыдущего слоя.

a l+1 =f( a l ,θ)

Здесь — матрица смежности, а f — определяющая функция. Каждый слой сверточной сети графа может быть записан с использованием этого выражения. Таким образом обычно работает сверточная нейронная сеть графа.

Приложения графовых сверточных сетей

• Графовые сверточные сети генерируют прогнозы для физических систем, таких как графы, их интерактивный подход и приложения. GCN также предоставляет точную информацию о свойствах объектов реального мира и физических систем (динамика столкновения, траектории объектов).
• GCN используются для решения задач дифференциации изображений. Модель, которой она следует, известна как «Обучение с нулевым выстрелом». Основной мотив этой модели состоит в том, чтобы идентифицировать неизвестное размеченное изображение и сгруппировать его в известные. Они также собирают семантическую информацию об этих ярлыках и классифицируют их.
• GCN могут принимать молекулярные отпечатки определенной длины в качестве входных данных и генерировать предсказанные молекулярные структуры. MolGAN — это один из видов сверточной сети графов, которая помогает создавать новые молекулярные структуры с различными функциями. Таким образом, это позволяет ученым изо дня в день изобретать современные молекулярные структуры.
• GCN применим для решения различных задач, связанных с исследовательскими операциями и приложениями комбинаторной оптимизации. Сверточные сети графов играют ключевую роль в решении задач продавца, задач квадратичного назначения и многих других. С помощью входного графа он может превзойти традиционные сложные алгоритмы.

Каратэ-клуб Закари

Еще одним важным применением графовых сверточных сетей является решение задач прогнозирования сообщества, таких как клуб каратэ Закари. В основе этой проблемы лежит спор между администратором и инструктором клуба.

Мы должны выяснить, какую сторону выберет каждый член клуба карате. Эта проблема решается с помощью методов полуконтролируемого обучения. Используя всего два помеченных узла, Тобиас Джепсен смог решить проблему и достичь почти идеальной точности прогнозирования этих двух сообществ.

Теперь давайте посмотрим на следующие изображения, и вы сможете получить некоторое представление о проблеме клуба каратэ и ее правильных расчетах с использованием графовых сверточных сетей.

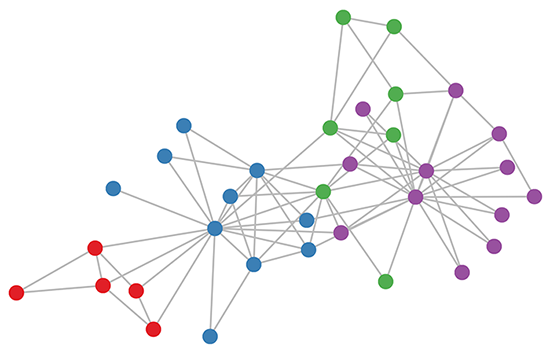
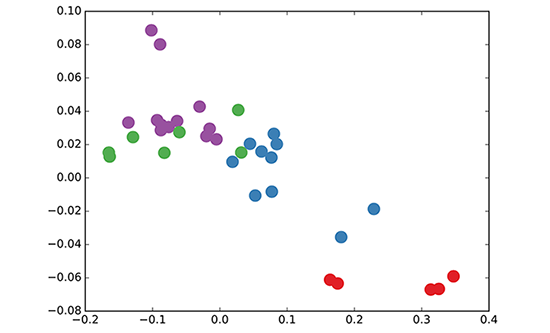
Источник изображения

Читайте также: Идеи проекта нейронной сети

Подведение итогов

Прочитав эту статью, вы сможете понять, что такое графовые сверточные сети, как строятся нейронные сети, получить краткое представление о GCN и о том, как он работает, а также о различных важных аспектах и ​​приложениях GCN, включая проблему Zachary Karate Club.

Если вы хотите узнать больше о GCN, его функциях и преимуществах, зарегистрируйтесь на сайте upGrad Education Pvt. Ltd. И курс для аспирантов и дипломов IIITB по машинному обучению и искусственному интеллекту . Этот курс по машинному обучению и искусственному интеллекту предназначен для студентов и работающих специалистов.

Курс предоставляет набор тематических исследований и заданий, отраслевые сессии наставничества, статус выпускника IIIT Bangalore, помощь в трудоустройстве в ведущих компаниях и, самое главное, богатый опыт обучения.