Sortarea în structura datelor: categorii și tipuri [cu exemple]

Aranjarea datelor într-o ordine preferată se numește sortare în structura datelor. Prin sortarea datelor, este mai ușor să căutați prin ele rapid și ușor. Cel mai simplu exemplu de sortare este un dicționar. Înainte de era internetului, când doreai să cauți un cuvânt într-un dicționar, o făceai în ordine alfabetică. Acest lucru a făcut ușor.

Imaginează-ți panica dacă ar trebui să treci printr-o carte mare cu toate cuvintele englezești din lume într-o ordine amestecată! Este aceeași panică prin care va trece un inginer dacă datele lor nu sunt sortate și structurate.

Deci, pe scurt, sortarea ne face viața mai ușoară. Consultați cursurile noastre de știință a datelor pentru a afla în profunzime algoritmii de știință a datelor.

În această postare, vă vom ghida prin diferitele structuri de date și algoritmi de sortare. Dar mai întâi, să înțelegem ce este un algoritm de sortare și sortarea în structura datelor.

Ce este un algoritm de sortare?

Un algoritm de sortare este doar o serie de comenzi sau instrucțiuni. În aceasta, o matrice este o intrare, pe care algoritmul de sortare efectuează operații pentru a oferi o matrice sortată.

Mulți copii ar fi învățat să sorteze structurile de date în orele de informatică. Este introdus într-un stadiu incipient pentru a ajuta copiii interesați să-și facă o idee despre subiecte mai profunde de informatică – metode împărțiți și cuceriți, arbori binari, grămezi etc.

Iată un exemplu despre ceea ce face sortarea.

Să presupunem că aveți o matrice de șiruri de caractere: [h,j,k,i,n,m,o,l]

Acum, sortarea ar produce o matrice de ieșire în ordine alfabetică.

Ieșire: [h,i,j,k,l,m,n,o]

Să aflăm mai multe despre sortarea în structura datelor.

Checkout: Tipuri de arbore binar

Sortarea categoriilor

Există două categorii diferite în sortare:

• Sortare internă : Dacă datele de intrare sunt astfel încât să poată fi ajustate în memoria principală dintr-o dată, se numește sortare internă.
• Sortare externă : Dacă datele de intrare sunt de așa natură încât nu pot fi ajustate în memorie în întregime simultan, trebuie să fie stocate pe un hard disk, dischetă sau orice alt dispozitiv de stocare. Aceasta se numește sortare externă.

Citiți: Idei și subiecte interesante pentru proiecte de structură a datelor

Tipuri de sortare în structura datelor

Iată câteva dintre cele mai comune tipuri de algoritmi de sortare.

1. Merge Sort

Acest algoritm funcționează la împărțirea unui tablou în două jumătăți de dimensiuni comparabile. Fiecare jumătate este apoi sortată și îmbinată împreună folosind funcția merge ().

Iată cum funcționează algoritmul:

MergeSort(arr[], l, r)

Dacă r > l

1. Împărțiți matricea în două jumătăți egale prin localizarea punctului din mijloc:

mijlocul m = (l+r)/2

2. Utilizați funcția mergeSort pentru a apela pentru prima jumătate:

Apelați mergeSort(arr, l, m)

3. Apelați mergeSort pentru a doua jumătate:

Apelați mergeSort(arr, m+1, r)

4. Utilizați funcția merge () pentru a îmbina cele două jumătăți sortate la pasul 2 și 3:

Apel merge(arr, l, m, r)

Consultați imaginea de mai jos pentru a obține o imagine clară a modului în care funcționează.

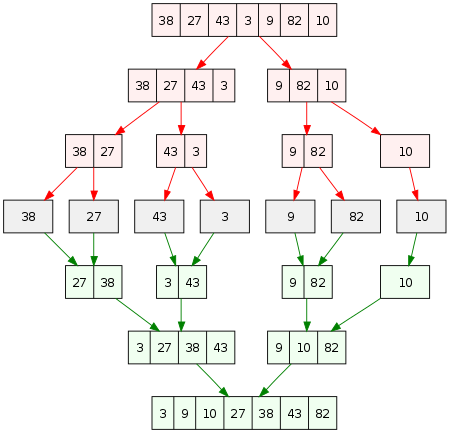
Sursă

Program Python pentru implementarea sortării îmbinării

def mergeSort(a):

dacă len(a) >1:

mid = len(a)//2

A = a[:mid]

B = a[mid:]

mergeSort(A)

mergeSort(B)

i = j = k = 0

în timp ce i < len(A) și j < len(B):

dacă A[i] < B[j]:

a[k] = A[i]

i+=1

altceva:

a[k] = B[j]

j+=1

k+=1

în timp ce i < len(A):

a[k] = A[i]

i+=1

k+=1

în timp ce j < len(R):

a[k] = B[j]

j+=1

k+=1

def printList(a):

pentru i în interval(len(a)):

print(a[i],end="")

imprimare()

if __name__ == '__main__':

a = [12, 11, 13, 5, 6, 7]

mergeSort(a)

print(„Matricea sortată este: „, end="\n”)

printList(a)

Aflați mai multe: Recursiune în structura datelor: cum funcționează, tipuri și când este utilizată

2. Sortare selecție

În aceasta, la început, cel mai mic element este trimis în prima poziție.

Apoi, următorul element cel mai mic este căutat în matricea rămasă și este plasat în a doua poziție. Acest lucru continuă până când algoritmul ajunge la elementul final și îl plasează în poziția corectă.

Privește imaginea de mai jos pentru a o înțelege mai bine.

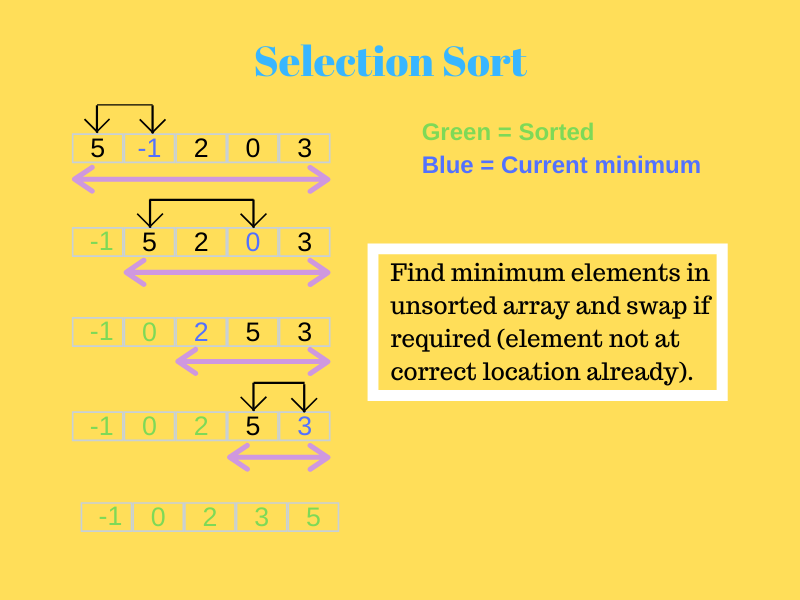Sursă

Program Python pentru implementarea sortării selecției

import sys

X = [6, 25, 10, 28, 11]

pentru i în interval(len(X)):

min_idx = i

pentru j în domeniul (i+1, len(X)):

dacă X[min_idx] > X[j]:

min_idx = j

X[i], X[min_idx] = X[min_idx], X[i]

print („Matricea sortată este”)

pentru i în interval(len(X)):

print(„%d” %X[i]),

Certificare avansată în știința datelor, peste 250 de parteneri de angajare, peste 300 de ore de învățare, 0% EMI

3. Sortare cu bule

Este cel mai simplu și mai simplu dintre toți algoritmii de sortare. Funcționează pe principiul schimbării repetate a elementelor adiacente în cazul în care acestea nu sunt în ordinea corectă.

În termeni mai simpli, dacă intrarea urmează să fie sortată în ordine crescătoare, sortarea cu bule va compara mai întâi primele două elemente din matrice. În cazul în care al doilea este mai mic decât primul, le va schimba pe cele două și va trece la următorul element și așa mai departe.

Exemplu :

Intrare : 637124

Prima trecere

63 7124 -> 36 7124 : Sortarea cu bule compară 6 și 3 și le schimbă pentru că 3<6.

3 67 124 -> 3 67 124 : De la 6<7, fără schimbare

36 71 24 -> 36 17 24 : Schimbat 7 și 1, ca 7>1

361 72 4 -> 361 27 4 : Schimbat 2 și 7, ca 2<7

3612 74 -> 3612 47 : Schimbat 4 și 7, ca 4<7

A doua trecere

36 1247 -> 36 1247

3 61 274 -> 3 16 274

31 62 74 -> 31 26 74

312 67 4 -> 312 67 4

3126 74 -> 3126 47

A treia trecere

31 2647 -> 13 2647

1 32 647 -> 1 23 647

12 36 47 -> 12 36 47

123 64 7 -> 123 46 7

1234 67 -> 1234 67

După cum puteți vedea, obținem rezultatul în ordine crescătoare după trei treceri.

Program Python pentru implementarea sortării cu bule

def bubbleSort(a):

n = len(a)

pentru i în intervalul (n):

pentru j în intervalul (0, ni-1):

dacă a[j] > a[j+1] :

a[j], a[j+1] = a[j+1], a[j]

a = [64, 34, 25, 12, 22, 11, 90]

bubbleSort(a)

print („Matricea sortată este:”)

pentru i în interval(len(a)):

tipăriți („%d” %a[i]),

Citiți și: Cadre de date în Python: Tutorial detaliat Python

Concluzie

Aceasta include sortarea în structura datelor și cei mai comuni algoritmi de sortare. Puteți alege oricare dintre diferitele tipuri de algoritmi de sortare. Cu toate acestea, amintiți-vă că unele dintre acestea pot fi puțin plictisitoare pentru a scrie programul. Dar apoi, ar putea fi utile pentru rezultate rapide. Pe de altă parte, dacă doriți să sortați seturi de date mari, trebuie să alegeți sortarea cu bule. Nu numai că oferă rezultate precise, dar este și ușor de implementat. Apoi, din nou, este mai lent decât celelalte tipuri. Sper că v-a plăcut articolul despre sortarea în structura datelor.

Pentru a obține mai multe informații despre cum funcționează sortarea, contactați-ne și vă vom ajuta să începeți cursul care se potrivește cel mai bine nevoilor dvs.!

Dacă sunteți curios să aflați despre știința datelor, consultați programul Executive PG în știința datelor de la IIIT-B și upGrad, care este creat pentru profesioniști care lucrează și oferă peste 10 studii de caz și proiecte, ateliere practice practice, mentorat cu experți din industrie, 1 -on-1 cu mentori din industrie, peste 400 de ore de învățare și asistență profesională cu firme de top.

Distrează-te la codificare!