O introducere în rețeaua neuronală Feedforward: straturi, funcții și importanță

Tehnologia de învățare profundă este coloana vertebrală a motoarelor de căutare, a traducerii automate și a aplicațiilor mobile. Funcționează prin imitarea creierului uman pentru a găsi și a crea modele din diferite tipuri de date.

O parte importantă a acestei tehnologii incredibile este o rețea neuronală feedforward, care ajută inginerii de software în recunoașterea și clasificarea modelelor, regresia neliniară și aproximarea funcției.

Să obținem câteva informații despre acest aspect esențial al arhitecturii rețelei neuronale de bază.

Ce este rețeaua neuronală Feedforward?

Cunoscută în mod obișnuit ca o rețea multistratificată de neuroni, rețelele neuronale feedforward sunt numite astfel datorită faptului că toată informația călătorește numai în direcția înainte.

Informația intră mai întâi în nodurile de intrare, se deplasează prin straturile ascunse și, în final, iese prin nodurile de ieșire. Rețeaua nu conține conexiuni pentru a alimenta informațiile care ies la nodul de ieșire înapoi în rețea.

Rețelele neuronale feedforward sunt menite să aproximeze funcțiile.

Iată cum funcționează .

Există un clasificator y = f*(x).

Aceasta introduce intrarea x în categoria y.

Rețeaua feedforward va mapa y = f (x; θ). Apoi memorează valoarea lui θ care aproximează cel mai bine funcția.

Rețea neuronală Feedforward pentru baza pentru recunoașterea obiectelor din imagini, așa cum puteți observa în aplicația Google Foto.

Straturile unei rețele neuronale feedforward

O rețea neuronală feedforward constă din următoarele.

Stratul de intrare

Conține neuronii de intrare-recepție. Apoi trec intrarea la stratul următor. Numărul total de neuroni din stratul de intrare este egal cu atributele din setul de date.

Strat ascuns

Acesta este stratul de mijloc, ascuns între straturile de intrare și de ieșire. Există un număr mare de neuroni în acest strat care aplică transformări intrărilor. Apoi îl transmit stratului de ieșire.

Stratul de ieșire

Este ultimul strat și depinde de construcția modelului. De asemenea, stratul de ieșire este caracteristica prezisă, deoarece știți care doriți să fie rezultatul.

Greutățile neuronilor

Puterea unei conexiuni între neuroni se numește greutăți. Valoarea unei greutăți variază de la 0 la 1.

Aflați mai multe: Model de rețea neuronală: scurtă introducere, glosar

Funcția de cost în rețeaua neuronală feedforward

Alegerea funcției de cost este una dintre cele mai importante părți ale unei rețele neuronale feedforward. De obicei, micile modificări ale ponderilor și părtinirilor nu afectează punctele de date clasificate. Deci, pentru a găsi o modalitate de a îmbunătăți performanța utilizând o funcție de cost fluidă pentru a face mici modificări la ponderi și părtiniri.

Formula pentru funcția de cost pentru eroarea pătrată medie este:

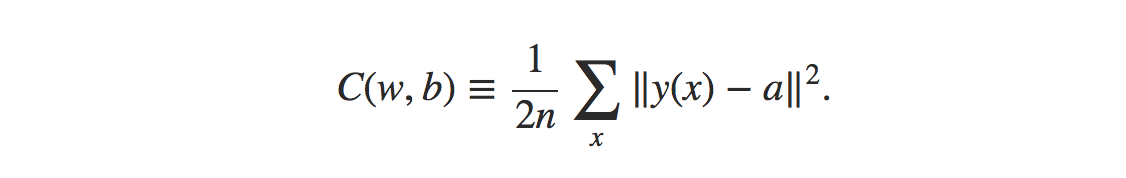
Sursă

Unde,

w = colectarea greutăților în rețea

b = prejudecăți

n = numărul de intrări de antrenament

a = vectori de ieșire

x = intrare

‖v‖ = lungimea obișnuită a vectorului v

Funcția de pierdere în rețeaua neuronală feedforward

Funcția de pierdere în rețeaua neuronală este menită să determine dacă există vreo corecție de care are nevoie procesul de învățare.

Neuronii stratului de ieșire vor fi egali cu numărul de clase. Pentru a compara diferența dintre distribuția probabilității prezisă și cea adevărată.

Pierderea de entropie încrucișată pentru clasificarea binară este:

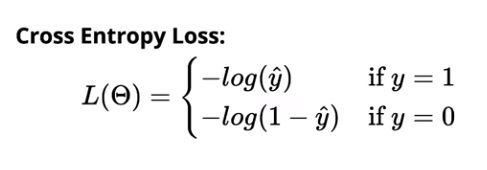
Pierderea de entropie încrucișată pentru clasificarea multiclasă este:

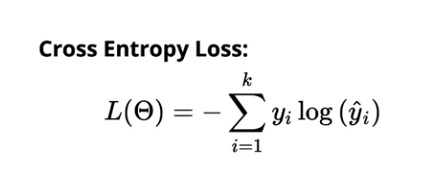
Sursă

Algoritmul de învățare cu gradient

Acest algoritm ajută la determinarea celor mai bune valori posibile pentru parametrii pentru a diminua pierderea în rețeaua neuronală feedforward.

Imagine

Toate ponderile (w₁₁₁, w₁₁₂,...) și prejudecățile b (b₁, b₂,....) sunt inițializate aleatoriu. Odată realizat acest lucru, observațiile din date sunt repetate. Apoi, distribuția prezisă corespunzătoare este determinată în funcție de fiecare observație. În cele din urmă, pierderea este calculată folosind funcția de entropie încrucișată.

Valoarea pierderii ajută apoi la calcularea modificărilor de făcut în greutăți pentru a reduce pierderea totală a modelului.

Citiți: 13 idei și subiecte interesante pentru proiecte de rețea neuronală

Nevoia unui model neuron

Să presupunem că intrările care sunt introduse în rețea sunt date brute de pixeli care provin dintr-o imagine scanată a unui personaj. Pentru ca rezultatul din rețea să clasifice corect cifra, ați dori să determinați cantitatea potrivită de ponderi și părtiniri.

Acum, ar trebui să faceți mici modificări la greutatea în rețea pentru a vedea cum ar funcționa învățarea. Pentru ca acest lucru să iasă perfect, mici modificări ale greutăților ar trebui să conducă doar la mici modificări ale producției.

Cu toate acestea, ce se întâmplă dacă modificarea mică a greutății echivalează cu o schimbare mare a producției? Modelul neuronului sigmoid poate rezolva o astfel de problemă.

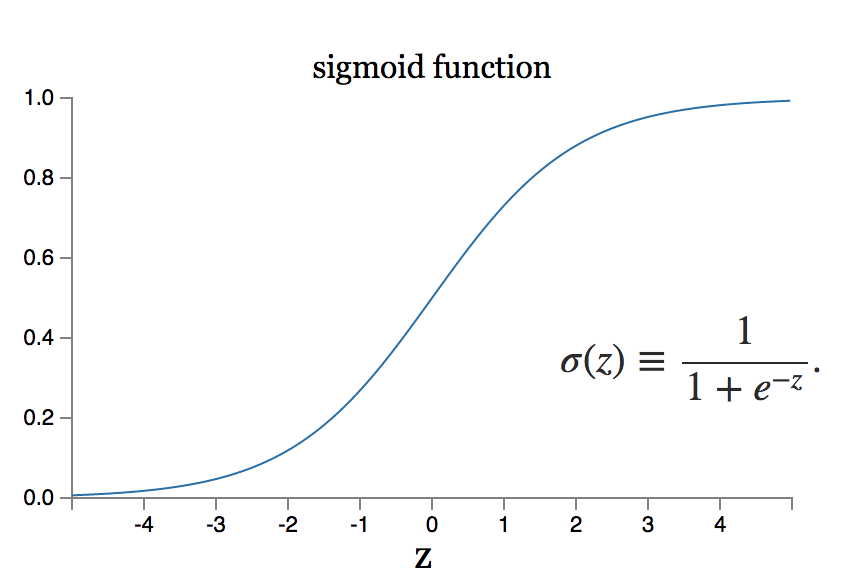
Sursă

Citește și: Cele 7 tipuri de rețele neuronale artificiale de care au nevoie inginerii ML

Concluzie

Învățarea profundă este un teritoriu al ingineriei software cu o amploare colosală de cercetare. Există o mulțime de arhitecturi de rețele neuronale actualizate pentru diferite tipuri de date. Sistemele neuronale convoluționale, de exemplu, au realizat cea mai bună execuție din clasă în domeniul procedurilor de manipulare a imaginilor, în timp ce sistemele neuronale recurente sunt în general utilizate în procesarea conținutului și a vocii.

În momentul în care sunt aplicate la seturi de date uriașe, sistemele neuronale au nevoie de măsuri monstruoase ale forței de calcul și ale accelerației echipamentelor, care pot fi realizate prin proiectarea amenajării unităților de procesare grafică sau a GPU-urilor. În cazul în care sunteți nou în utilizarea GPU-urilor, puteți descoperi setări configurate gratuite pe web. Cele mai preferate sunt caietele Kaggle sau Google Collab Notebooks.

Pentru a realiza o rețea neuronală feedforward eficientă, efectuați mai multe iterații în arhitectura rețelei, care necesită multă testare.

Pentru mai multe informații despre cum funcționează aceste rețele, aflați de la experții de la upGrad. Cursurile noastre sunt incredibil de cuprinzătoare și vă puteți rezolva întrebările luând direct legătura cu profesorii noștri experimentați și cei mai buni din clasă.

Dacă sunteți interesat să aflați mai multe despre învățarea automată, consultați Diploma PG de la IIIT-B și upGrad în Învățare automată și AI, care este concepută pentru profesioniști care lucrează și oferă peste 450 de ore de pregătire riguroasă, peste 30 de studii de caz și sarcini, IIIT- B Statut de absolvenți, peste 5 proiecte practice practice și asistență pentru locuri de muncă cu firme de top.