Tri dans la structure de données : catégories et types [avec exemples]

La disposition des données dans un ordre préféré est appelée tri dans la structure de données. En triant les données, il est plus facile de les parcourir rapidement et facilement. L'exemple le plus simple de tri est un dictionnaire. Avant l'ère d'Internet, lorsque vous vouliez rechercher un mot dans un dictionnaire, vous le faisiez par ordre alphabétique. Cela a facilité la tâche.

Imaginez la panique si vous deviez parcourir un gros livre avec tous les mots anglais du monde dans un ordre confus ! C'est la même panique que traversera un ingénieur si ses données ne sont pas triées et structurées.

Bref, le tri nous facilite la vie. Consultez nos cours de science des données pour en savoir plus sur les algorithmes de science des données.

Dans cet article, nous vous expliquerons les différentes structures de données et algorithmes de tri. Mais d'abord, comprenons ce qu'est un algorithme de tri et le tri dans la structure des données.

Qu'est-ce qu'un algorithme de tri ?

Un algorithme de tri n'est qu'une série d'ordres ou d'instructions. En cela, un tableau est une entrée, sur laquelle l'algorithme de tri effectue des opérations pour donner un tableau trié.

De nombreux enfants auraient appris à trier des structures de données dans leurs cours d'informatique. Il est introduit à un stade précoce pour aider les enfants intéressés à se faire une idée des sujets informatiques plus approfondis - méthodes de division pour mieux régner, arbres binaires, tas, etc.

Voici un exemple de ce que fait le tri.

Supposons que vous ayez un tableau de chaînes : [h,j,k,i,n,m,o,l]

Maintenant, le tri donnerait un tableau de sortie dans l'ordre alphabétique.

Sortie : [h,i,j,k,l,m,n,o]

Apprenons-en plus sur le tri dans la structure des données.

Paiement : Types d'arbre binaire

Catégories de tri

Il existe deux catégories différentes dans le tri :

• Tri interne : Si les données d'entrée sont telles qu'elles peuvent être ajustées en une seule fois dans la mémoire principale, on parle de tri interne.
• Tri externe : Si les données d'entrée sont telles qu'elles ne peuvent pas être entièrement ajustées dans la mémoire en une seule fois, elles doivent être stockées sur un disque dur, une disquette ou tout autre périphérique de stockage. C'est ce qu'on appelle le tri externe.

Lire : Idées et sujets intéressants pour les projets de structure de données

Types de tri dans la structure de données

Voici quelques-uns des types d'algorithmes de tri les plus courants.

1. Fusionner le tri

Cet algorithme fonctionne en divisant un tableau en deux moitiés de tailles comparables. Chaque moitié est ensuite triée et fusionnée à l'aide de la fonction merge ().

Voici comment fonctionne l'algorithme :

FusionTrie(arr[], l, r)

Si r > l

1. Divisez le tableau en deux moitiés égales en localisant le point médian :

milieu m = (l+r)/2

2. Utilisez la fonction mergeSort pour appeler la première moitié :

Appelez mergeSort(arr, l, m)

3. Appelez mergeSort pour la seconde moitié :

Appeler mergeSort(arr, m+1, r)

4. Utilisez la fonction merge () pour fusionner les deux moitiés triées aux étapes 2 et 3 :

Appeler la fusion (arr, l, m, r)

Consultez l'image ci-dessous pour obtenir une image claire de la façon dont cela fonctionne.

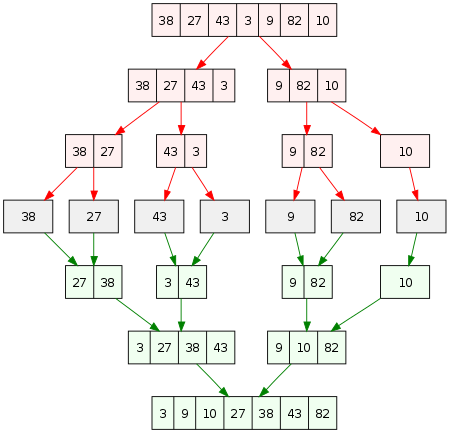
La source

programme Python pour l'implémentation du tri par fusion

def mergeSort(a):

si len(a) >1 :

milieu = len(a)//2

A = a[:moyen]

B = un[moyen :]

fusionTri(A)

fusionTri(B)

je = j = k = 0

tandis que i < len(A) et j < len(B) :

si A[i] < B[j] :

a[k] = A[i]

je+=1

autre:

a[k] = B[j]

j+=1

k+=1

tant que je < len(A):

a[k] = A[i]

je+=1

k+=1

tant que j < len(R) :

a[k] = B[j]

j+=1

k+=1

def printList(a):

pour je dans la plage (len (a)):

print(a[i],end=" ")

impression()

si __nom__ == '__main__' :

un = [12, 11, 13, 5, 6, 7]

fusionTri(a)

print("Le tableau trié est : ", end="\n")

printList(a)

En savoir plus : Récursion dans la structure de données : comment ça marche, les types et quand ils sont utilisés

2. Tri de sélection

En cela, dans un premier temps, le plus petit élément est envoyé à la première position.

Ensuite, le plus petit élément suivant est recherché dans le tableau restant et est placé à la deuxième position. Cela continue jusqu'à ce que l'algorithme atteigne l'élément final et le place dans la bonne position.

Regardez l'image ci-dessous pour mieux comprendre.

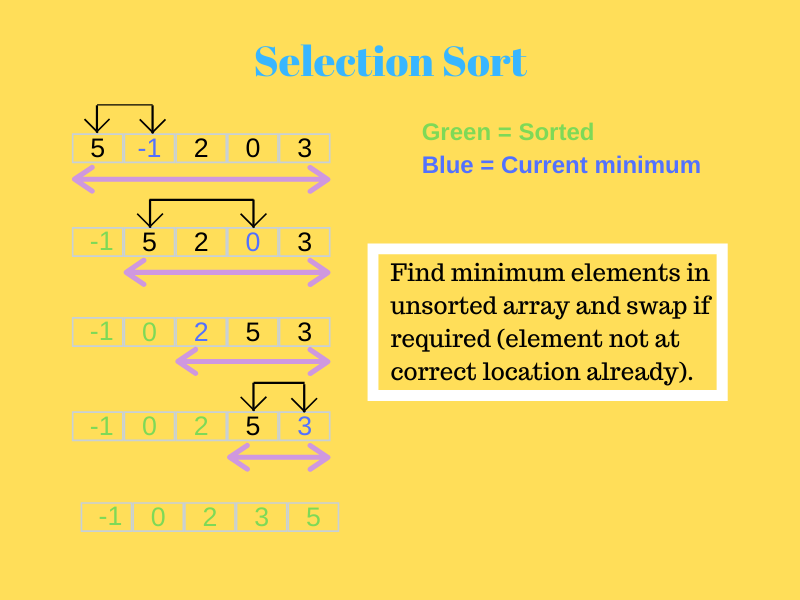La source

programme Python pour l'implémentation du tri par sélection

importer système

X = [6, 25, 10, 28, 11]

pour je dans la plage (len (X)):

min_idx = je

pour j dans la plage(i+1, len(X)) :

si X[min_idx] > X[j] :

min_idx = j

X[i], X[min_idx] = X[min_idx], X[i]

print ("Le tableau trié est")

pour je dans la plage (len (X)):

print("%d" %X[i]),

Certification avancée en science des données, plus de 250 partenaires d'embauche, plus de 300 heures d'apprentissage, 0 % EMI

3. Tri à bulles

C'est le plus simple et le plus simple de tous les algorithmes de tri. Il fonctionne sur le principe de l'échange répété d'éléments adjacents au cas où ils ne seraient pas dans le bon ordre.

En termes plus simples, si l'entrée doit être triée par ordre croissant, le tri à bulles comparera d'abord les deux premiers éléments du tableau. Dans le cas où le second est plus petit que le premier, il permutera les deux, et passera à l'élément suivant, et ainsi de suite.

Exemple :

Entrée : 637124

Premier passage

63 7124 -> 36 7124 : Le tri à bulles compare 6 et 3 et les échange car 3<6.

3 67 124 -> 3 67 124 : Depuis 6<7, pas d'échange

36 71 24 -> 36 17 24 : Permutation 7et 1, comme 7>1

361 72 4 -> 361 27 4 : Échange 2 et 7, car 2<7

3612 74 -> 3612 47 : Permutation 4 et 7, comme 4<7

Deuxième passe

36 1247 -> 36 1247

3 61 274 -> 3 16 274

31 62 74 -> 31 26 74

312 67 4 -> 312 67 4

3126 74 -> 3126 47

Troisième passe

31 2647 -> 13 2647

1 32 647 -> 1 23 647

12 36 47 -> 12 36 47

123 64 7 -> 123 46 7

1234 67 -> 1234 67

Comme vous pouvez le voir, nous obtenons le résultat de l'ordre croissant après trois passages.

programme Python pour l'implémentation du tri à bulles

def bubbleSort(a):

n = len(a)

pour i dans la plage (n):

pour j dans la plage (0, ni-1):

si a[j] > a[j+1] :

a[j], a[j+1] = a[j+1], a[j]

un = [64, 34, 25, 12, 22, 11, 90]

bubbleSort(a)

print ("Le tableau trié est :")

pour je dans la plage (len (a)):

imprimer ("%d" %a[i]),

Lisez également : Data Frames in Python : Python In-depth Tutorial

Conclusion

Cela termine le tri dans la structure des données et les algorithmes de tri les plus courants. Vous pouvez choisir l'un des différents types d'algorithmes de tri. Cependant, rappelez-vous que certains d'entre eux peuvent être un peu fastidieux pour écrire le programme. Mais alors, ils pourraient être utiles pour des résultats rapides. En revanche, si vous souhaitez trier de grands ensembles de données, vous devez choisir le tri à bulles. Non seulement il donne des résultats précis, mais il est également facile à mettre en œuvre. Là encore, il est plus lent que les autres types. J'espère que vous avez aimé l'article sur le tri dans la structure des données.

Pour en savoir plus sur le fonctionnement du tri, contactez-nous et nous vous aiderons à démarrer le cours qui correspond le mieux à vos besoins !

Si vous êtes curieux d'en savoir plus sur la science des données, consultez le programme Executive PG en science des données de IIIT-B & upGrad qui est créé pour les professionnels en activité et propose plus de 10 études de cas et projets, des ateliers pratiques, un mentorat avec des experts de l'industrie, 1 -on-1 avec des mentors de l'industrie, plus de 400 heures d'apprentissage et d'aide à l'emploi avec les meilleures entreprises.

Amusez-vous à coder !