データ構造での並べ替え：カテゴリとタイプ[例付き]

データを優先順に配置することを、データ構造の並べ替えと呼びます。 データを並べ替えることで、データをすばやく簡単に検索できます。 並べ替えの最も簡単な例は辞書です。 インターネットの時代以前は、辞書で単語を検索したいときは、アルファベット順に検索していました。 これで簡単になりました。

あなたが世界からのすべての英語の単語をごちゃ混ぜに並べた大きな本を読まなければならなかったら、パニックを想像してみてください！ データがソートおよび構造化されていない場合、エンジニアが経験するのと同じパニックです。

つまり、並べ替えによって私たちの生活が楽になります。 データサイエンスのアルゴリズムについて詳しく知るには、データサイエンスのコースをご覧ください。

この投稿では、さまざまなデータ構造と並べ替えアルゴリズムについて説明します。 ただし、最初に、並べ替えアルゴリズムとは何か、およびデータ構造での並べ替えについて理解しましょう。

並べ替えアルゴリズムとは何ですか？

並べ替えアルゴリズムは、一連の注文または指示にすぎません。 この場合、配列は入力であり、その上で並べ替えアルゴリズムが操作を実行して、並べ替えられた配列を出力します。

多くの子供たちは、コンピュータサイエンスのクラスでデータ構造を分類することを学んだでしょう。 分割統治法、二分木、ヒープなど、関心のある子供たちがより深いコンピュータサイエンスのトピックについて理解できるように、早い段階で導入されています。

並べ替えの例を次に示します。

文字列の配列があるとしましょう：[h、j、k、i、n、m、o、l]

これで、並べ替えにより、アルファベット順に出力配列が生成されます。

出力：[h、i、j、k、l、m、n、o]

データ構造での並べ替えについて詳しく見ていきましょう。

チェックアウト：二分木の種類

カテゴリの並べ替え

並べ替えには2つの異なるカテゴリがあります。

• 内部ソート：入力データがメインメモリで一度に調整できるようなものである場合、それは内部ソートと呼ばれます。
• 外部ソーティング：入力データがメモリ内で一度に完全に調整できないようなものである場合は、ハードディスク、フロッピーディスク、またはその他のストレージデバイスに保存する必要があります。 これは外部ソーティングと呼ばれます。

読む：興味深いデータ構造プロジェクトのアイデアとトピック

データ構造での並べ替えの種類

並べ替えアルゴリズムの最も一般的なタイプのいくつかを次に示します。

1.マージソート

このアルゴリズムは、配列を同等のサイズの2つの半分に分割する際に機能します。 次に、各半分が並べ替えられ、merge（）関数を使用してマージされます。

アルゴリズムの仕組みは次のとおりです。

MergeSort（arr []、l、r）

r>lの場合

1. 中間点を見つけて、配列を2つの等しい半分に分割します。

真ん中のm=（l + r）/ 2

2. mergeSort関数を使用して、前半を呼び出します。

mergeSort（arr、l、m）を呼び出します

3. 後半はmergeSortを呼び出します。

mergeSort（arr、m + 1、r）を呼び出します

4. マージ（）関数を使用して、ステップ2と3でソートされた2つの半分をマージします。

merge（arr、l、m、r）を呼び出す

下の画像をチェックして、これがどのように機能するかを明確に把握してください。

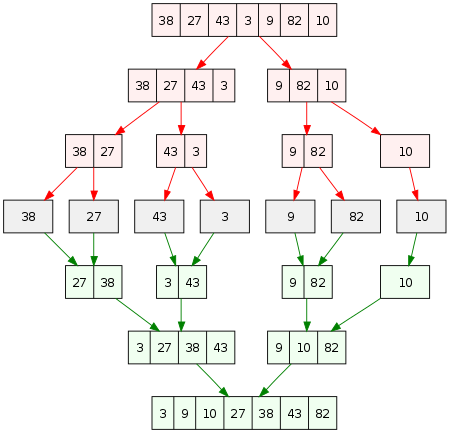
ソース

マージソート実装用のPythonプログラム

def mergeSort（a）：

len（a）> 1の場合：

mid = len（a）// 2

A = a [：mid]

B = a [mid：]

mergeSort（A）

mergeSort（B）

i = j = k = 0

i <len（A）およびj <len（B）の場合：

A [i] <B [j]の場合：

a [k] = A [i]

i + = 1

そうしないと：

a [k] = B [j]

j + = 1

k + = 1

i <len（A）：

a [k] = A [i]

i + = 1

k + = 1

一方、j <len（R）：

a [k] = B [j]

j + = 1

k + = 1

def printList（a）：

範囲内のiの場合（len（a））：

print（a [i]、end =”“）

print（）

if __name__ =='__main__'：

a = [12、11、13、5、6、7]

mergeSort（a）

print（“ソートされた配列は：“、end =” \ n”）

printList（a）

詳細：データ構造の再帰：どのように機能するか、タイプと使用時期

2.選択ソート

この場合、最初に、最小の要素が最初の位置に送信されます。

次に、残りの配列で次に小さい要素が検索され、2番目の位置に配置されます。 これは、アルゴリズムが最後の要素に到達し、それを正しい位置に配置するまで続きます。

それをよりよく理解するために下の写真を見てください。

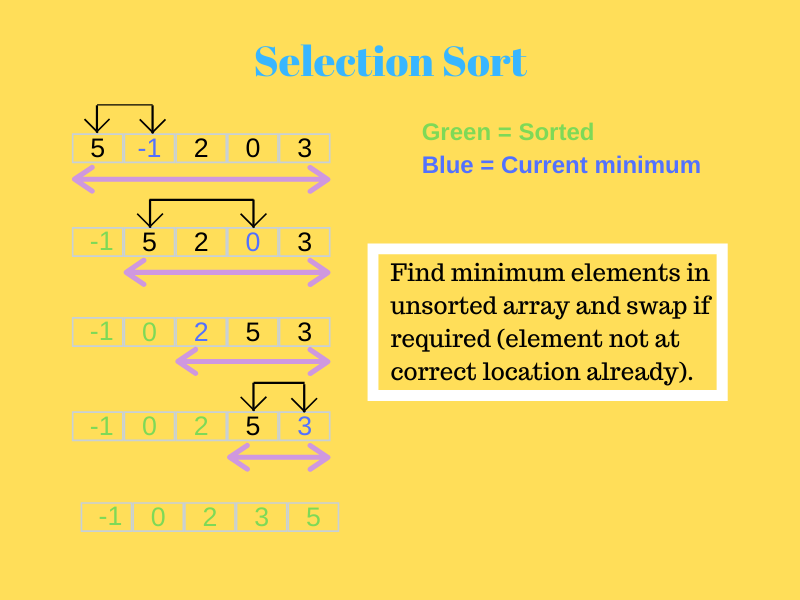ソース

選択ソート実装用のPythonプログラム

sysをインポート

X = [6、25、10、28、11]

for i in range（len（X））：

min_idx = i

range（i + 1、len（X））のjの場合：

X [min_idx]> X [j]の場合：

min_idx = j

X [i]、X [min_idx] = X [min_idx]、X [i]

print（「ソートされた配列は」）

for i in range（len（X））：

print（“％d”％X [i]）、

データサイエンスの高度な認定、250以上の採用パートナー、300時間以上の学習、0％EMI

3.バブルソート

これは、すべての並べ替えアルゴリズムの中で最も簡単で単純です。 隣接する要素が正しい順序でない場合に、それらを繰り返し交換するという原則に基づいて機能します。

簡単に言うと、入力を昇順で並べ替える場合、バブルソートは最初に配列の最初の2つの要素を比較します。 2番目の要素が最初の要素よりも小さい場合は、2つを入れ替えて、次の要素に移動します。

例：

入力：637124

初回通過

63 7124-> 36 7124：バブルソートは6と3を比較し、3<6であるためそれらを交換します。

3 67124- > 3 67124 ：6 <7なので、スワッピングなし

36 71 24-> 36 17 24：7>1として7と1を入れ替えた

361 72 4-> 361 27 4：2<7として2と7を入れ替えた

3612 74- > 3612 47 ：4<7として4と7を入れ替えた

2回目のパス

36 1247-> 36 1247

3 61274- > 3 16274

31 62 74-> 31 26 74

312 67 4-> 312 67 4

3126 74- > 3126 47

3回目のパス

31 2647-> 13 2647

1 32 647-> 1 23 647

12 36 47-> 12 36 47

123 64 7-> 123 46 7

1234 67- > 1234 67

ご覧のとおり、3回のパスで昇順の結果が得られます。

バブルソート実装のためのPythonプログラム

defbubbleSort（a）：

n = len（a）

範囲（n）のiの場合：

range（0、ni-1）のjの場合：

a [j]> a [j + 1]の場合：

a [j]、a [j + 1] = a [j + 1]、a [j]

a = [64、34、25、12、22、11、90]

バブルソート（a）

print（「ソートされた配列は次のとおりです：」）

範囲内のiの場合（len（a））：

印刷（“％d”％a [i]）、

また読む： Pythonのデータフレーム：Pythonの詳細なチュートリアル

結論

これで、データ構造と最も一般的な並べ替えアルゴリズムでの並べ替えが完了します。 さまざまな種類の並べ替えアルゴリズムのいずれかを選択できます。 ただし、これらのいくつかは、プログラムを作成するのに少し面倒な場合があることを覚えておいてください。 しかし、その後、それらは迅速な結果のために役立つかもしれません。 一方、大きなデータセットを並べ替える場合は、バブルソートを選択する必要があります。 正確な結果が得られるだけでなく、実装も簡単です。 繰り返しになりますが、他のタイプよりも低速です。 データ構造の並べ替えに関する記事が気に入っていただけたでしょうか。

並べ替えがどのように機能するかについてより多くの洞察を得るために、私たちに連絡してください。私たちはあなたがあなたのニーズに最も適したコースを始めるのを手伝います！

データサイエンスについて知りたい場合は、IIIT-B＆upGradのデータサイエンスのエグゼクティブPGプログラムをチェックしてください。これは、働く専門家向けに作成され、10以上のケーススタディとプロジェクト、実践的なハンズオンワークショップ、業界の専門家とのメンターシップを提供します。1業界のメンターとの1対1、400時間以上の学習、トップ企業との仕事の支援。

コーディングを楽しんでください！