Sortieren in der Datenstruktur: Kategorien & Typen [mit Beispielen]

Die Anordnung von Daten in einer bevorzugten Reihenfolge wird in der Datenstruktur als Sortierung bezeichnet. Durch das Sortieren von Daten ist es einfacher, sie schnell und einfach zu durchsuchen. Das einfachste Beispiel für das Sortieren ist ein Wörterbuch. Wenn Sie vor der Ära des Internets ein Wort in einem Wörterbuch nachschlagen wollten, taten Sie dies in alphabetischer Reihenfolge. Das machte es einfach.

Stellen Sie sich die Panik vor, wenn Sie ein großes Buch mit allen englischen Wörtern aus der Welt in einer durcheinandergebrachten Reihenfolge durchgehen müssten! Es ist die gleiche Panik, die ein Ingenieur durchmachen wird, wenn seine Daten nicht sortiert und strukturiert sind.

Kurz gesagt, das Sortieren erleichtert unser Leben. Sehen Sie sich unsere Data-Science-Kurse an, um mehr über Data-Science-Algorithmen zu erfahren.

In diesem Beitrag führen wir Sie durch die verschiedenen Datenstrukturen und Sortieralgorithmen. Aber zuerst wollen wir verstehen, was ein Sortieralgorithmus ist und in der Datenstruktur sortieren.

Was ist ein Sortieralgorithmus?

Ein Sortieralgorithmus ist nur eine Reihe von Befehlen oder Anweisungen. Dabei ist ein Array eine Eingabe, an der der Sortieralgorithmus Operationen ausführt, um ein sortiertes Array auszugeben.

Viele Kinder hätten im Informatikunterricht gelernt, Datenstrukturen einzuordnen. Es wird frühzeitig eingeführt, um interessierten Kindern einen Einblick in tiefere Informatikthemen zu geben – Teile-und-Herrsche-Methoden, Binärbäume, Haufen usw.

Hier ist ein Beispiel dafür, was das Sortieren bewirkt.

Nehmen wir an, Sie haben ein Array von Strings: [h,j,k,i,n,m,o,l]

Jetzt würde das Sortieren ein Ausgabearray in alphabetischer Reihenfolge ergeben.

Ausgabe: [h,i,j,k,l,m,n,o]

Lassen Sie uns mehr über das Sortieren in der Datenstruktur erfahren.

Checkout: Arten von Binärbäumen

Kategorien sortieren

Beim Sortieren gibt es zwei unterschiedliche Kategorien:

• Interne Sortierung : Wenn die Eingabedaten so sind, dass sie sofort im Hauptspeicher angepasst werden können, spricht man von interner Sortierung.
• Externes Sortieren : Wenn die Eingabedaten so sind, dass sie nicht vollständig auf einmal im Speicher angepasst werden können, müssen sie auf einer Festplatte, einer Diskette oder einem anderen Speichergerät gespeichert werden. Dies wird als externe Sortierung bezeichnet.

Lesen Sie: Interessante Ideen und Themen für Datenstrukturprojekte

Arten der Sortierung in der Datenstruktur

Hier sind einige der häufigsten Arten von Sortieralgorithmen.

1. Sortieren zusammenführen

Dieser Algorithmus arbeitet daran, ein Array in zwei Hälften vergleichbarer Größe aufzuteilen. Jede Hälfte wird dann sortiert und mithilfe der Funktion merge () wieder zusammengeführt.

So funktioniert der Algorithmus:

MergeSort(arr[], l, r)

Wenn r > l

1. Teilen Sie das Array in zwei gleiche Hälften, indem Sie den Mittelpunkt bestimmen:

Mitte m = (l+r)/2

2. Verwenden Sie die Funktion mergeSort, um die erste Hälfte aufzurufen:

Aufruf mergeSort(arr, l, m)

3. Rufen Sie mergeSort für die zweite Hälfte auf:

Aufruf mergeSort(arr, m+1, r)

4. Verwenden Sie die Funktion merge (), um die beiden in Schritt 2 und 3 sortierten Hälften zusammenzuführen:

Zusammenführen von Anrufen (arr, l, m, r)

Schauen Sie sich das Bild unten an, um ein klares Bild davon zu bekommen, wie das funktioniert.

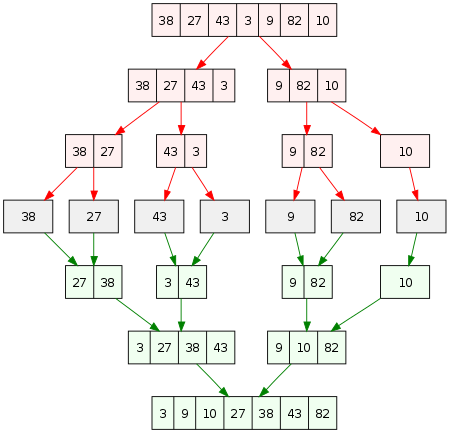
Quelle

Python-Programm für die Implementierung von Merge-Sortierung

def mergeSort(a):

wenn len(a) >1:

mitte = len(a)//2

A = a[:mitte]

B = a[Mitte:]

mergeSort(A)

mergeSort(B)

ich = j = k = 0

während i < len(A) und j < len(B):

wenn A[i] < B[j]:

a[k] = A[i]

i+=1

anders:

a[k] = B[j]

j+=1

k+=1

während i < len(A):

a[k] = A[i]

i+=1

k+=1

während j < len(R):

a[k] = B[j]

j+=1

k+=1

def printList(a):

für i im Bereich(len(a)):

print(a[i],end=" ")

drucken()

if __name__ == '__main__':

a = [12, 11, 13, 5, 6, 7]

mergeSort(a)

print("Sortiertes Array ist: ", end="\n")

printList(a)

Erfahren Sie mehr: Rekursion in der Datenstruktur: Funktionsweise, Typen und Verwendung

2. Auswahl sortieren

Dabei wird zunächst das kleinste Element an die erste Position geschickt.

Dann wird das nächstkleinere Element im verbleibenden Array gesucht und an die zweite Position gesetzt. Dies wird so lange fortgesetzt, bis der Algorithmus das letzte Element erreicht und es an der richtigen Position platziert.

Schauen Sie sich das Bild unten an, um es besser zu verstehen.

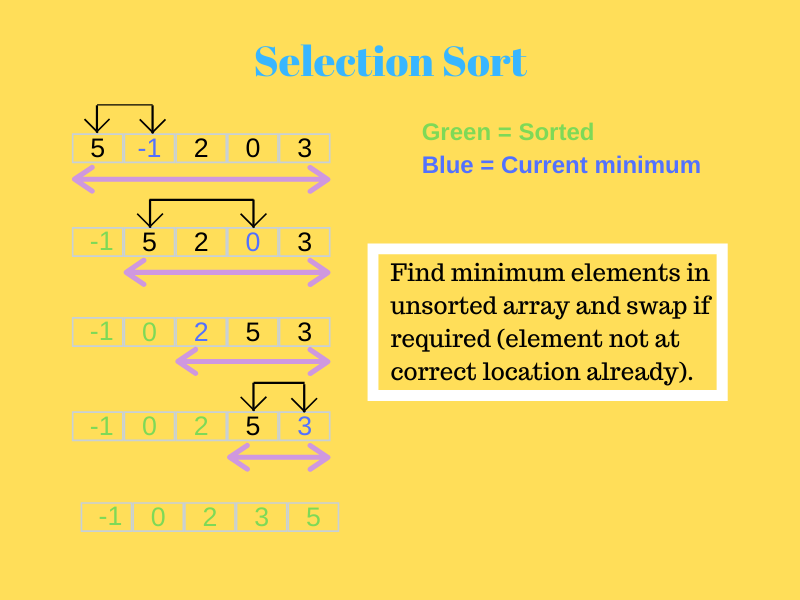Quelle

Python-Programm für die Implementierung der Auswahlsortierung

System importieren

X = [6, 25, 10, 28, 11]

für i im Bereich(len(X)):

min_idx = ich

für j in range(i+1, len(X)):

wenn X[min_idx] > X[j]:

min_idx = j

X[i], X[min_idx] = X[min_idx], X[i]

print („Das sortierte Array ist“)

für i im Bereich(len(X)):

print("%d" %X[i]),

Data Science Advanced-Zertifizierung, über 250 Einstellungspartner, über 300 Lernstunden, 0 % EMI

3. Blasensortierung

Es ist der einfachste und einfachste aller Sortieralgorithmen. Es funktioniert nach dem Prinzip, benachbarte Elemente wiederholt zu vertauschen, falls sie nicht in der richtigen Reihenfolge sind.

Einfacher ausgedrückt, wenn die Eingabe in aufsteigender Reihenfolge sortiert werden soll, vergleicht die Blasensortierung zuerst die ersten beiden Elemente im Array. Falls das zweite kleiner als das erste ist, werden die beiden vertauscht und zum nächsten Element übergegangen, und so weiter.

Beispiel :

Eingabe : 637124

Erster Pass

63 7124 -> 36 7124 : Bubblesort vergleicht 6 und 3 und vertauscht sie, weil 3<6.

3 67 124 -> 3 67 124 : Seit 6<7 kein Austausch

36 71 24 -> 36 17 24 : 7 und 1 vertauscht, da 7>1

361 72 4 -> 361 27 4 : 2 und 7 vertauscht, da 2<7

3612 74 -> 3612 47 : 4 und 7 vertauscht, da 4<7

Zweiter Durchgang

36 1247 -> 36 1247

3 61 274 -> 3 16 274

31 62 74 -> 31 26 74

312 67 4 -> 312 67 4

3126 74 -> 3126 47

Dritter Durchgang

31 2647 -> 13 2647

1 32 647 -> 1 23 647

12 36 47 -> 12 36 47

123 64 7 -> 123 46 7

1234 67 -> 1234 67

Wie Sie sehen können, erhalten wir das Ergebnis der aufsteigenden Reihenfolge nach drei Durchgängen.

Python-Programm für die Bubble-Sort-Implementierung

def bubbleSort(a):

n = len(a)

für i im Bereich (n):

für j im Bereich (0, ni-1):

wenn a[j] > a[j+1] :

a[j], a[j+1] = a[j+1], a[j]

a = [64, 34, 25, 12, 22, 11, 90]

bubbleSort(a)

print ("Das sortierte Array ist:")

für i im Bereich(len(a)):

drucken („%d“ %a[i]),

Lesen Sie auch: Datenrahmen in Python: Ausführliches Python-Tutorial

Fazit

Damit sind das Sortieren in der Datenstruktur und die gängigsten Sortieralgorithmen abgeschlossen. Sie können eine der verschiedenen Arten von Sortieralgorithmen auswählen. Denken Sie jedoch daran, dass es für einige davon etwas mühsam sein kann, das Programm zu schreiben. Aber dann könnten sie für schnelle Ergebnisse nützlich sein. Wenn Sie hingegen große Datensätze sortieren möchten, müssen Sie die Blasensortierung wählen. Es liefert nicht nur genaue Ergebnisse, sondern ist auch einfach zu implementieren. Andererseits ist es langsamer als die anderen Typen. Ich hoffe, Ihnen hat der Artikel über das Sortieren in der Datenstruktur gefallen.

Um mehr Einblicke in die Funktionsweise des Sortierens zu erhalten, wenden Sie sich an uns und wir helfen Ihnen beim Einstieg in den Kurs, der Ihren Bedürfnissen am besten entspricht!

Wenn Sie neugierig sind, etwas über Data Science zu lernen, schauen Sie sich das Executive PG Program in Data Science von IIIT-B & upGrad an, das für Berufstätige entwickelt wurde und mehr als 10 Fallstudien und Projekte, praktische Workshops, Mentoring mit Branchenexperten, 1 -on-1 mit Branchenmentoren, mehr als 400 Stunden Lern- und Jobunterstützung bei Top-Unternehmen.

Viel Spaß beim Codieren!