グラフ畳み込みネットワーク：知っておく必要のあるアプリケーションのリスト

畳み込みネットワークはニューラルネットワークの一種です。 ニューラルネットワークは、特別な種類の深層学習モデルです。 通常、機械学習または深層学習は、その複雑なタスクのために、厳密で高価なアルゴリズムで構成されます。 同様に、グラフの深層学習モデルはさらに複雑です。 グラフ畳み込みネットワークは、主に画像分類の目的で使用されます。 畳み込みニューラルネットワークの詳細をご覧ください。

過去10年間で、データサイエンスのアプリケーションは大幅に増加しました。 このデータが豊富な世界では、学習モデルのアプローチにより、優れた結果と正確な予測がもたらされました。 グラフは多くの情報システムに役立ちます。

生物学的タンパク質の相互作用からインターネット接続やWorldWideWebまで、グラフはこれらすべてのシステムを表しています。 また、グラフィカル構造を介してニューラルネットワークを実装すると、コンピューターは画像のプロパティを理解できます。 このモデルは、グラフの最も高度な実際のアプリケーションの1つです。 これらのアルゴリズムについて詳しく説明しましょう。

ニューラルネットワークの構築方法

ニューラルネットワークは、データサイエンスとディープラーニングの最先端技術の1つです。 ニューラルネットワークは、株式市場の予測から画像分類、音声または文字認識、さらにはシーケンス分析まで、多くのアプリケーションで役立ちます。

ニューラルネットワークの最初の概念は、生物学的観点から生まれました。 科学者たちは、視覚のための神経が脳の聴覚中枢に接続されている実験を行いました。 最終的に、生物は脳の聴覚センターを通しても見ることを学びました。 さらに実験を重ねると、脳のすべての中心がすべての行動を実行できることが証明されました。

アプローチは、コンピュータアルゴリズムに情報を提供する人間の脳を模倣し始めました。 したがって、同様に、コンピューター科学者も、すべてのコンピューター脳学習問題を解決できる単一のアルゴリズムが必要であると考えました。 このようにしてニューラルネットワークが誕生しました。

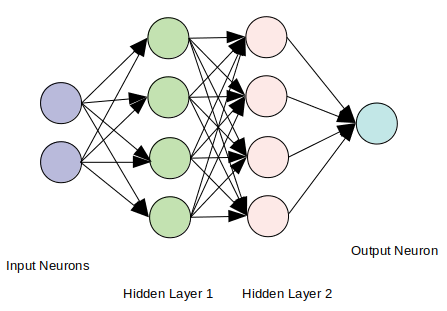
ニューラルネットワークは、ニューロンの複数の層で構成されています。 各ニューロンは通常、グラフノードです。 各層の各ニューロンは、重み付きエッジを介して次の層のすべてのニューロンに接続されています。エッジの重みは、層の値の計算の係数として機能します。

バックプロパゲーションにより、係数はモデルをサンプルトレーニングの例に合わせるために変更されます。 最終的に、最後の層からの単一のニューロンが出力を提供します。 次の画像では、ニューラルネットワークの構造を説明しています。

画像ソース

読む：画像分類のための畳み込みニューラルネットワークの使用

グラフ畳み込みネットワーク

畳み込みネットワークは、3次元ニューラルネットワークです。 畳み込みニューラルネットワークの最も実用的な用途には、画像の分類と認識、自然言語処理、音声認識などがあります。 これらのモデルは通常、通常の2次元ニューラルネットワークモデルよりも複雑です。

このアーキテクチャでは、さまざまなニューロンの層が組み立てられます。 ディメンションのパラメーターは、モデルにパラメーターを認識させるために、さまざまなレイヤーで可変です。 たとえば、画像は2次元であり、その間、各ポイントの色も重要な役割を果たします。 したがって、3つの異なるパラメータが出現します。 このような複雑さに対処するために、ConvNetsは重要な役割を果たします。

異なる次元のこれらの多くの3D行列は、ニューラルネットワークの複数のレベルで機能します。 最終的に、「z」次元はネットワークの出力パラメーターに適合します。 あるレベルから別のレベルへの情報の伝達は、さまざまな異なるアルゴリズムを介して行うことができます。

たとえば、FC（Fully Connected）、Pooling、およびReLUは、これに関するいくつかの重要なアルゴリズムです。

一般に、ニューラルネットワークのノード値はで示されます。ここで、「l」は層番号を示します。 したがって、 0は入力行列です。

a 0 = X

一方、最後のレイヤーノードは出力を定義します。 たとえば、「L」レイヤーがあります。 したがって、 Lはニューラルネットワークの出力を示します。

a L = Y

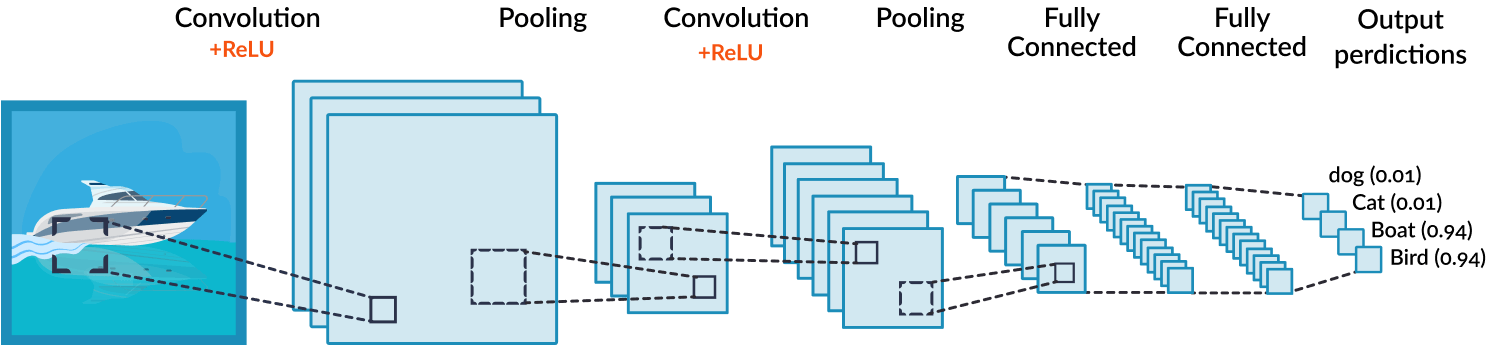
画像ソース

上の画像は、画像分類の実装における畳み込みニューラルネットワークを示しています。 パラメータは、犬、猫、コウモリ、鳥に設定されています。

特定の内部レイヤーのノード値は、前のレイヤー値から計算されます。

a l + 1 = f（ a l 、θ）

ここで、は隣接行列であり、 fは定義関数です。 すべてのグラフ畳み込みネットワーク層は、この式を使用して記述できます。 このように、グラフ畳み込みニューラルネットワークは通常機能します。

グラフ畳み込みネットワークのアプリケーション

• グラフ畳み込みネットワークは、グラフ、そのインタラクティブなアプローチ、アプリケーションなどの物理システムに関する予測を生成します。 GCNは、実世界のエンティティと物理システムのプロパティ（衝突のダイナミクス、オブジェクトの軌道）に関する正確な情報も提供します。
• GCNは、画像の微分問題を実行するために使用されます。 それが従うモデルは「ゼロショット学習」として知られています。 このモデルの主な動機は、未知のラベル付き画像を識別し、それを既知の画像にグループ化することです。 また、これらのラベルのセマンティック情報を収集して分類します。
• GCNは、特定の長さの分子フィンガープリントを入力として受け取り、予測される分子構造を生成できます。 MolGANは、グラフ畳み込みネットワークの一種であり、さまざまな機能を備えた新しい分子構造を作成するのに役立ちます。 このようにして、科学者は毎日現代の分子構造を発明することができます。
• GCNは、研究業務や組み合わせ最適化アプリケーションに関連するさまざまな問題の解決に適用できます。 グラフ畳み込みネットワークは、セールスマンの問題、二次割り当ての問題などを解決する上で極めて重要な役割を果たします。 入力グラフの助けを借りて、それは従来の複雑なアルゴリズムを凌駕することができます。

ザカリー空手クラブ

グラフ畳み込みネットワークのもう1つの重要なアプリケーションは、ザカリーの空手クラブなどのコミュニティ予測の問題を解決することです。 この問題は、クラブの管理者とインストラクターの間の論争に基づいています。

空手クラブのすべてのメンバーがどちらの側を選択するかを理解する必要があります。 この問題は、半教師あり学習手法を使用することで解決されます。 Tobias Jepsenは、ラベル付けされた2つのノードを使用するだけで、問題を修正し、これら2つのコミュニティを予測するという点でほぼ完全な精度に到達することができました。

次に、次の画像を見てみましょう。グラフ畳み込みネットワークを使用して、空手クラブの問題とその適切な計算についていくつかの洞察を得ることができます。

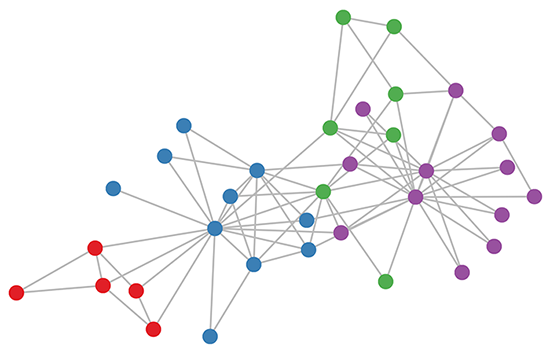
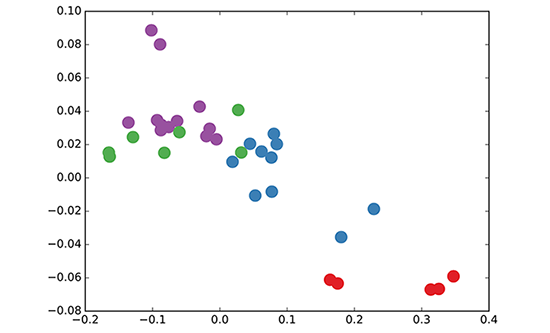
画像ソース

また読む：ニューラルネットワークプロジェクトのアイデア

まとめ

この記事を読むことで、グラフ畳み込みネットワークとは何か、ニューラルネットワークの構築方法、GCNの簡単なアイデアとその仕組み、ZacharyKarateClubの問題を含むGCNのさまざまな重要な側面とアプリケーションを理解できます。

GCNとその機能および利点について詳しく知りたい場合は、 upGradEducationPvtに登録してください。 Ltd.とIIITBの機械学習と人工知能に関する大学院および卒業証書コース。 機械学習とAIに関するこのコースは、学生と働く専門家を対象としています。

このコースでは、ケーススタディと課題のコレクション、業界のメンターシップセッション、IIIT Bangaloreの卒業生のステータス、トップ企業との就職支援、そして最も重要なこととして、豊富な学習経験を提供します。