Une introduction au réseau de neurones Feedforward : couches, fonctions et importance
Publié: 2020-05-28La technologie d'apprentissage en profondeur est l'épine dorsale des moteurs de recherche, de la traduction automatique et des applications mobiles. Il fonctionne en imitant le cerveau humain pour trouver et créer des modèles à partir de différents types de données.
Une partie importante de cette incroyable technologie est un réseau de neurones à anticipation, qui aide les ingénieurs en logiciel dans la reconnaissance et la classification des modèles, la régression non linéaire et l'approximation des fonctions.
Voyons un peu cet aspect essentiel de l'architecture du réseau de neurones de base.
Table des matières
Qu'est-ce que le réseau de neurones Feedforward ?
Communément appelés réseaux multicouches de neurones, les réseaux de neurones à anticipation sont appelés ainsi en raison du fait que toutes les informations ne circulent que dans le sens direct.
Les informations entrent d'abord dans les nœuds d'entrée, se déplacent à travers les couches cachées et sortent finalement par les nœuds de sortie. Le réseau ne contient aucune connexion pour renvoyer les informations sortant au nœud de sortie dans le réseau.
Les réseaux de neurones feedforward sont destinés à approximer les fonctions.

Voici comment cela fonctionne .
Il existe un classifieur y = f*(x).
Cela alimente l'entrée x dans la catégorie y.
Le réseau d'anticipation mappera y = f (x; θ). Il mémorise alors la valeur de θ qui se rapproche le mieux de la fonction.
Réseau de neurones feedforward pour la base de la reconnaissance d'objets dans les images, comme vous pouvez le constater dans l'application Google Photos.
Les couches d'un réseau de neurones Feedforward
Un réseau neuronal prédictif se compose des éléments suivants.
Couche d'entrée
Il contient les neurones récepteurs d'entrée. Ils transmettent ensuite l'entrée à la couche suivante. Le nombre total de neurones dans la couche d'entrée est égal aux attributs de l'ensemble de données.
Couche masquée
Il s'agit de la couche intermédiaire, cachée entre les couches d'entrée et de sortie. Il y a un grand nombre de neurones dans cette couche qui appliquent des transformations aux entrées. Ils le transmettent ensuite à la couche de sortie.
Couche de sortie
C'est la dernière couche et dépend de la construction du modèle. De plus, la couche de sortie est l'entité prédite car vous savez ce que vous voulez que le résultat soit.
Poids des neurones
La force d'une connexion entre les neurones est appelée poids. La valeur d'un poids est comprise entre 0 et 1.
En savoir plus : Modèle de réseau de neurones : brève introduction, glossaire
Fonction de coût dans le réseau de neurones Feedforward
Le choix de la fonction de coût est l'une des parties les plus importantes d'un réseau de neurones à anticipation. Habituellement, de petits changements dans les pondérations et les biais n'affectent pas les points de données classés. Donc, pour trouver un moyen d'améliorer les performances en utilisant une fonction de coût lisse pour apporter de petites modifications aux pondérations et aux biais.
La formule de la fonction de coût de l'erreur quadratique moyenne est :
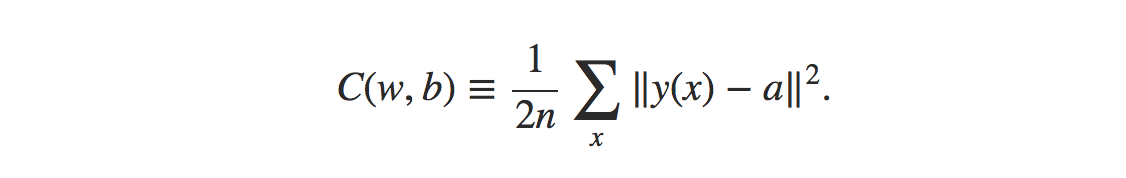
La source
Où,
w = collection de poids dans le réseau
b = biais
n = nombre d'entrées de formation
a = vecteurs de sortie
x = entrée
‖v‖ = longueur habituelle du vecteur v
Fonction de perte dans le réseau de neurones Feedforward
La fonction de perte dans le réseau neuronal est destinée à déterminer s'il y a une correction dont le processus d'apprentissage a besoin.
Les neurones de la couche de sortie seront égaux au nombre de classes. Pour comparer la différence entre la distribution de probabilité prédite et vraie.
La perte d'entropie croisée pour la classification binaire est :
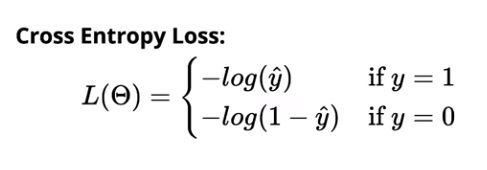
La perte d'entropie croisée pour la classification multi-classes est :

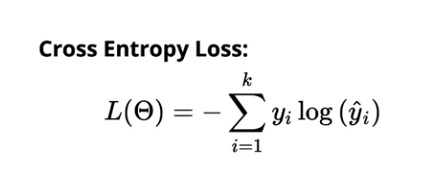
La source
Algorithme d'apprentissage de gradient
Cet algorithme permet de déterminer toutes les meilleures valeurs possibles pour les paramètres afin de diminuer la perte dans le réseau de neurones à anticipation.

Image
Tous les poids (w₁₁₁, w₁₁₂,…) et biais b (b₁, b₂,….) sont initialisés aléatoirement. Une fois cela fait, les observations dans les données sont itérées. Ensuite, la distribution prédite correspondante est déterminée par rapport à chaque observation. Enfin, la perte est calculée à l'aide de la fonction d'entropie croisée.
La valeur de perte aide ensuite à déterminer les modifications à apporter aux poids pour diminuer la perte globale du modèle.
Lire : 13 idées et sujets intéressants pour les projets de réseau de neurones
Le besoin d'un modèle neuronal
Disons que les entrées introduites dans le réseau sont des données de pixels brutes provenant d'une image numérisée d'un personnage. Pour que la sortie dans le réseau classe correctement le chiffre, vous voudriez déterminer la bonne quantité de poids et de biais.
Maintenant, vous auriez besoin d'apporter de petites modifications au poids dans le réseau pour voir comment l'apprentissage fonctionnerait. Pour que cela se passe parfaitement, de petits changements dans les poids ne doivent entraîner que de petits changements dans la sortie.
Cependant, que se passe-t-il si le petit changement de poids équivaut à un grand changement de sortie ? Le modèle de neurone sigmoïde peut résoudre un tel problème.
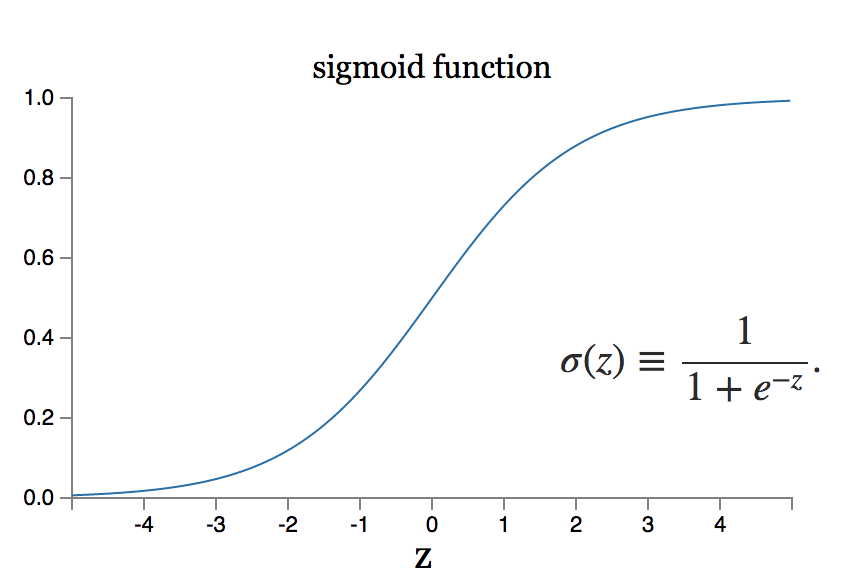
La source
Lisez aussi : Les 7 types de réseaux de neurones artificiels dont les ingénieurs ML ont besoin

Conclusion
L'apprentissage en profondeur est un territoire du génie logiciel avec une étendue de recherche colossale. Il existe de nombreuses architectures de réseaux de neurones actualisées pour différents types de données. Les systèmes neuronaux convolutifs, par exemple, ont accompli la meilleure exécution de leur catégorie dans les domaines des procédures de traitement d'images, tandis que les systèmes neuronaux récurrents sont généralement utilisés dans le traitement du contenu et de la voix.
Lorsqu'ils sont appliqués à d'énormes ensembles de données, les systèmes neuronaux ont besoin de mesures monstrueuses de la force de calcul et de l'accélération de l'équipement, ce qui peut être réalisé grâce à la conception d'unités de traitement graphique ou de GPU. Si vous débutez dans l'utilisation des GPU, vous pouvez découvrir des paramètres configurés gratuitement sur le Web. Les plus préférés sont les blocs-notes Kaggle ou les blocs-notes Google Collab.
Pour réaliser un réseau de neurones à anticipation efficace, vous effectuez plusieurs itérations dans l'architecture du réseau, ce qui nécessite de nombreux tests.
Pour plus d'informations sur le fonctionnement de ces réseaux, informez-vous auprès des experts d'upGrad. Nos cours sont incroyablement complets et vous pouvez résoudre vos questions en contactant directement nos professeurs expérimentés et les meilleurs de leur catégorie.
Si vous souhaitez en savoir plus sur l'apprentissage automatique, consultez le diplôme PG en apprentissage automatique et IA de IIIT-B & upGrad, conçu pour les professionnels en activité et offrant plus de 450 heures de formation rigoureuse, plus de 30 études de cas et missions, IIIT- Statut B Alumni, plus de 5 projets de synthèse pratiques et aide à l'emploi avec les meilleures entreprises.
L'algèbre linéaire est-elle nécessaire dans les réseaux de neurones ?
Un réseau de neurones est un modèle mathématique qui résout n'importe quel problème complexe. Le réseau prend un ensemble d'entrées et calcule un ensemble de sorties dans le but d'atteindre le résultat souhaité. Lors de l'étude de la théorie des réseaux de neurones, la majorité des neurones et des couches sont fréquemment formatés en algèbre linéaire. L'algèbre linéaire est nécessaire pour construire le modèle mathématique. Vous pouvez également utiliser l'algèbre linéaire pour comprendre la mise en réseau du modèle. Ainsi, pour répondre à la question, oui, la connaissance de base de l'algèbre linéaire est obligatoire lors de l'utilisation des réseaux de neurones.
Qu'entend-on par rétropropagation dans les réseaux de neurones ?
Dans le cas des réseaux de neurones qui utilisent la descente de gradient, la rétropropagation est utilisée. Cet algorithme estime le gradient de la fonction d'erreur par rapport aux poids du réseau de neurones et est essentiellement une propagation vers l'arrière des erreurs. Cette approche est utilisée car le réglage fin des poids réduit les taux d'erreur et améliore ainsi la généralisation du modèle de réseau neuronal, le rendant plus fiable. La rétropropagation est généralement classée comme une forme d'apprentissage automatique supervisé, car elle nécessite un résultat connu et prévu pour chaque valeur d'entrée afin de calculer le gradient de la fonction de perte dans les réseaux de neurones.
En quoi la rétropropagation est-elle différente des optimiseurs ?
Dans les réseaux de neurones, les optimiseurs et l'algorithme de rétropropagation sont utilisés, et ils fonctionnent ensemble pour rendre le modèle plus fiable. La rétropropagation est utilisée pour calculer efficacement les gradients, et les optimiseurs sont utilisés pour entraîner le réseau de neurones à l'aide des gradients obtenus à l'aide de la rétropropagation. En un mot, ce que la rétropropagation fait pour nous, c'est de calculer des gradients, qui sont ensuite utilisés par les optimiseurs.
