Réseaux convolutifs de graphes : liste des applications que vous devez connaître

Le réseau convolutif est un type de réseau de neurones. Les réseaux de neurones sont un type particulier de modèle d'apprentissage en profondeur. En règle générale, l'apprentissage automatique ou l'apprentissage en profondeur comprend des algorithmes rigoureux et coûteux en raison de sa tâche compliquée. De même, les modèles d'apprentissage en profondeur sur les graphes sont encore plus compliqués. Les réseaux convolutifs de graphes sont principalement utilisés à des fins de classification d'images. En savoir plus sur les réseaux de neurones convolutifs.

Au cours de la dernière décennie, l'application de la science des données a énormément augmenté. Dans ce monde riche en données, l'approche du modèle d'apprentissage a apporté d'excellents résultats et des prédictions précises. Les graphiques sont utiles pour de nombreux systèmes d'information.

Des interactions protéiques biologiques à la connectivité Internet et au WorldWideWeb, les graphiques représentent tous ces systèmes. De plus, la mise en œuvre de réseaux de neurones via une structure graphique permet à l'ordinateur de comprendre les propriétés d'une image. Ce modèle est l'une des applications réelles les plus avancées du graphe. Détaillons ces algorithmes :

Comment les réseaux de neurones sont construits

Les réseaux de neurones sont l'une des techniques les plus avancées de la science des données et de l'apprentissage en profondeur. Les réseaux de neurones sont utiles dans de nombreuses applications, de la prédiction boursière à la classification d'images, à la reconnaissance de la parole ou de caractères et même à l'analyse de séquences.

Le premier concept du réseau de neurones est venu des perspectives biologiques. Les scientifiques ont mené des expériences dans lesquelles les nerfs de la vision sont connectés aux centres auditifs du cerveau. Finalement, l'organisme a également appris à voir à travers le centre auditif du cerveau. Même d'autres expériences ont prouvé que chaque centre du cerveau pouvait effectuer chaque action.

Les approches ont commencé à imiter le cerveau humain informant les algorithmes informatiques. Ainsi, de la même manière, les informaticiens ont également pensé qu'il devrait y avoir un seul algorithme capable de résoudre tous les problèmes d'apprentissage du cerveau informatique. C'est ainsi que le réseau de neurones est né.

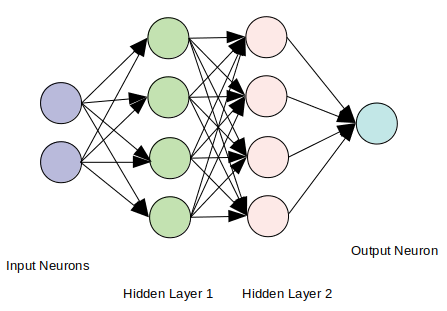
Un réseau de neurones est constitué de plusieurs couches de neurones. Chaque neurone est typiquement un nœud de graphe. Chaque neurone de chaque couche est connecté à tous les neurones de la couche suivante par un bord pondéré - les poids du bord agissent comme un coefficient du calcul de la valeur de la couche.

Grâce à la rétropropagation, les coefficients changent pour s'adapter au modèle avec des exemples d'apprentissage. En fin de compte, un seul neurone de la dernière couche donne la sortie. Dans l'image suivante, la structure d'un réseau de neurones est expliquée.

Source des images

Lire : Utilisation d'un réseau de neurones convolutifs pour la classification d'images

Réseaux convolutifs de graphes

Les réseaux convolutifs sont des réseaux de neurones tridimensionnels. La plupart des utilisations pratiques des réseaux de neurones convolutifs incluent la classification et la reconnaissance d'images, le traitement du langage naturel et la reconnaissance vocale. Ces modèles sont généralement plus complexes que les modèles de réseaux de neurones bidimensionnels habituels.

Dans cette architecture, des couches de neurones différents sont assemblées. Le paramètre de dimensions est variable dans différentes couches pour que le modèle reconnaisse les paramètres. Par exemple, les images sont en deux dimensions et, en attendant, la couleur de chaque point joue également un rôle crucial. Ainsi, trois paramètres différents émergent. Pour faire face à de telles complexités, les Conv Nets jouent un rôle important.

Ces nombreuses matrices 3D de différentes dimensions fonctionnent à plusieurs niveaux du réseau de neurones. Finalement, la dimension 'z' correspond au paramètre de sortie du réseau. La transmission d'informations d'un niveau à un autre peut s'effectuer à travers une variété d'algorithmes différents.

Par exemple, FC (Fully Connected), Pooling et ReLU sont des algorithmes cruciaux à cet égard.

Généralement, les valeurs de nœud du réseau neuronal sont désignées par, où « l » signifie le numéro de couche. Ainsi, un 0 est la matrice d'entrée.

un 0 =X

D'autre part, le dernier nœud de couche définit la sortie. Supposons qu'il existe des couches « L ». Par conséquent , un L désigne la sortie du réseau neuronal.

un L =Y

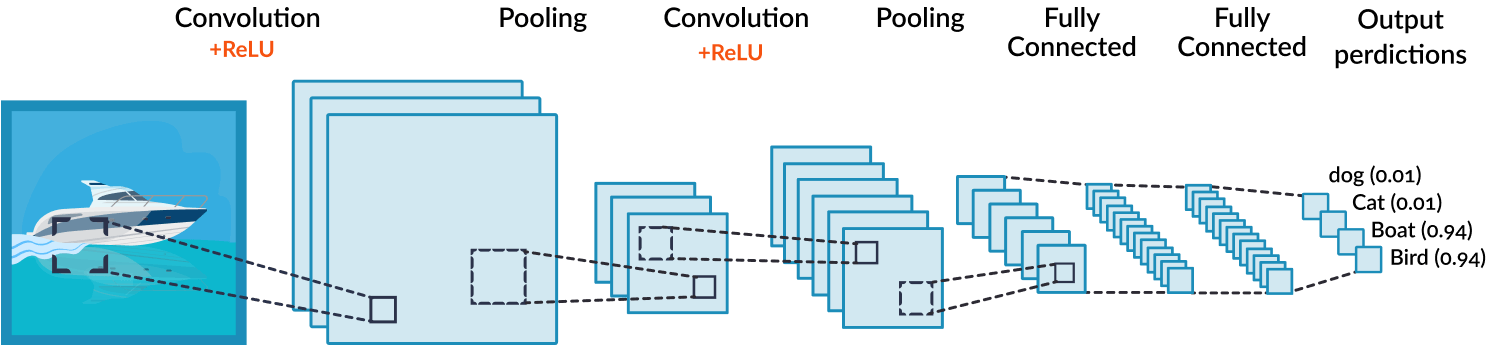
Source des images

L'image ci-dessus représente un réseau neuronal convolutif dans la mise en œuvre de la classification d'images. Les paramètres sont définis pour un chien, un chat, une chauve-souris et un oiseau.

La valeur de nœud d'une couche interne particulière est calculée à partir des valeurs de couche précédentes.

une l+1 =f( une l ,θ)

Ici, est la matrice d'adjacence et, f est la fonction de définition. Chaque couche de réseau convolutionnel de graphe peut être écrite à l'aide de cette expression. De cette manière, un réseau de neurones à convolution graphique fonctionne généralement.

Applications des réseaux convolutionnels de graphes

• Les réseaux convolutifs de graphes génèrent des prédictions sur des systèmes physiques, tels que des graphes, leur approche interactive et leurs applications. GCN fournit également des informations précises sur les propriétés des entités du monde réel et des systèmes physiques (dynamique de la collision, trajectoires des objets).
• Les GCN sont utilisés pour effectuer des problèmes de différenciation d'images. Le modèle qu'il suit est connu sous le nom de "Zero-Shot Learning". Le motif principal de ce modèle est d'identifier une image étiquetée inconnue et de la regrouper en images connues. Ils recueillent également des informations sémantiques sur ces étiquettes et les catégorisent.
• Les GCN peuvent prendre une certaine longueur d'empreintes moléculaires en entrée et générer des structures moléculaires prédites. MolGAN est un type de réseau Graph Convolutional qui aide à créer de nouvelles structures moléculaires avec diverses caractéristiques. De cette façon, il permet aux scientifiques d'inventer jour après jour des structures moléculaires modernes.
• GCN est applicable pour résoudre divers problèmes liés aux opérations de recherche et aux applications d'optimisation combinatoire. Les réseaux convolutifs de graphes jouent un rôle central dans la résolution des problèmes de vendeur, des problèmes d'affectation quadratique et bien d'autres. Avec l'aide du graphe d'entrée, il peut surclasser les algorithmes complexes traditionnels.

Club de Karaté de Zachary

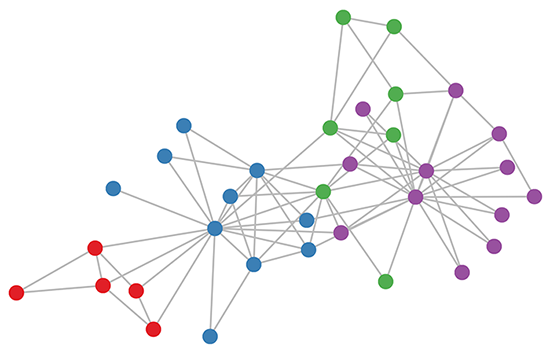
Une autre application importante des réseaux convolutifs de graphes consiste à résoudre des problèmes de prédiction communautaire, tels que le Karate Club of Zachary. Ce problème est basé sur le différend entre l'administrateur et l'instructeur du club.

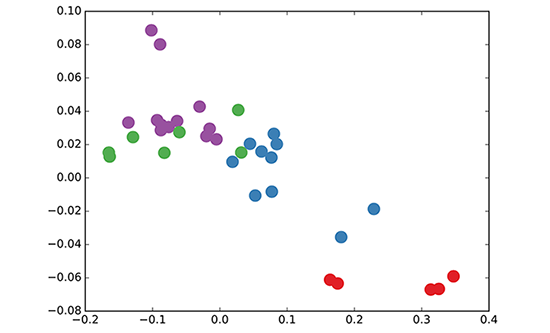
Nous devons déterminer quel côté chaque membre du club de karaté choisirait. Ce problème est résolu en utilisant des techniques d'apprentissage semi-supervisé. En utilisant seulement deux nœuds étiquetés, Tobias Jepsen a pu résoudre le problème et atteindre une précision presque parfaite en termes de prédiction de ces deux communautés.

Examinons maintenant les images suivantes et vous pourrez obtenir des informations sur le problème du club de karaté et ses calculs appropriés à l'aide des réseaux convolutifs de graphes.

Source des images

Lisez aussi: Idées de projets de réseau neuronal

Emballer

En lisant cet article, vous pourrez comprendre ce que sont les réseaux convolutifs de graphes, comment les réseaux de neurones sont construits, une brève idée de GCN et de son fonctionnement, ainsi que divers aspects et applications cruciaux de GCN, y compris le problème du Zachary Karate Club.

Si vous souhaitez en savoir plus sur GCN, ses fonctionnalités et ses avantages, inscrivez-vous sur upGrad Education Pvt. Ltd. Et le cours de troisième cycle et de diplôme de l'IIITB sur l'apprentissage automatique et l'intelligence artificielle . Ce cours sur l'apprentissage automatique et l'IA est conçu pour les étudiants et les professionnels en activité.

Le cours fournit une collection d'études de cas et de missions, des sessions de mentorat de l'industrie, le statut d'ancien élève de l'IIIT Bangalore, une aide au placement dans les meilleures entreprises et, plus important encore, une riche expérience d'apprentissage.