線性回歸與。 邏輯回歸:線性回歸和邏輯回歸之間的區別
已發表: 2020-09-10如果沒有兩種最簡單的機器學習算法,機器學習的世界將是不完整的。 是的,線性回歸和邏輯回歸都是您可以實現的最直接的機器學習算法。 在討論線性回歸和邏輯回歸之間的任何區別之前,我們必須首先了解這兩種算法的基礎。
首先,這兩種算法本質上都是監督學習。 這意味著,您將提供給這兩種算法的數據應該被很好地標記。 另一個需要注意的關鍵是用例。 馬上,這兩種算法之間的一個明顯區別是兩者的用例。 每當我們想要執行回歸時,都會使用線性回歸。 這意味著,每當我們想要預測連續數字時,我們都會使用線性回歸,例如特定區域的房價。
但是,邏輯回歸的使用是在分類問題中完成的。 這意味著,如果我們想預測特定房子是昂貴還是便宜(而不是價格),我們使用邏輯回歸算法。 是的,即使邏輯回歸的名稱中有回歸這個詞,它也用於分類。
您將在下面找到更多這樣令人興奮的微妙之處。 但在正面比較線性回歸與邏輯回歸之前,讓我們首先了解有關這些算法的更多信息。
目錄
線性回歸
線性回歸是最容易理解和部署的機器學習算法。 它是一種監督學習算法,因此如果我們想要預測連續值(或執行回歸),我們必須使用標記良好的數據集為該算法提供服務。 這種機器學習算法是最直接的,因為它具有線性特性。 為了成功預測未來值,線性回歸嘗試通過輸入算法的數據形成一條直線。
因此,每當將任何信息輸入線性回歸算法時,它都會獲取數據並獲取直線方程,隨機選擇斜率和截距,直到找到最佳擬合線。 如果我們輸入該算法的數據僅包含一個自變量,則稱為簡單線性回歸。

另一方面,如果數據具有多個自變量,則回歸變為多元線性回歸。 線性回歸的數學形式很簡單,如下所示。
y= a0+a1x+ c
這裡,y 是因變量,a0 和 a1 是該算法任務要找到的係數,x 是因變量,c 是這條直線的截距值。
邏輯回歸
毋庸置疑,邏輯回歸是監督學習算法下最直接但功能最強大的分類機器學習算法之一。 該算法可用於回歸問題,但主要用於解決分類問題。 我們從該算法獲得的輸出始終介於 0 和 1 之間,因此使用閾值分類值將實例分類為類變得毫不費力。

名稱中的邏輯一詞是指激活函數,在此回歸中使用。 在這種情況下,激活函數或邏輯函數實際上只是 sigmoid 函數。 這是這個 sigmoid 函數的特性,它使邏輯回歸的值始終在零和一之間。 sigmoid 函數看起來像這樣:
![]()
這裡,y 是通過 sigmoid 函數的輸出,x 是自變量。 在邏輯回歸的情況下,變量 x 實際上是整個線性回歸方程。 因此,可以開發邏輯回歸方程,如下所示:

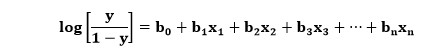
這裡,變量的含義與邏輯回歸中的類似,x是自變量,y是因變量,b0、b1、b2等是該算法確定的係數。
線性回歸和邏輯回歸之間的區別
下面列出了線性回歸與邏輯回歸的綜合比較:
| 線性回歸 | 邏輯回歸 |
| 它需要標記良好的數據,這意味著它需要監督,並且用於回歸。 因此,線性回歸是一種有監督的回歸算法。 | 它還要求輸入的數據進行良好的標記。 但是,該算法用於分類而不是回歸。 所以邏輯回歸是一種有監督的分類算法。 |
| 通過線性回歸算法得到的預測值通常可以在負無窮到正無窮的範圍內。 | 通過邏輯回歸獲得的預測實際上在零到一的範圍內。 此功能允許在閾值的幫助下輕鬆分類。 |
| 線性回歸不需要激活函數。 | 這裡我們需要一個激活函數。 在這種情況下,該函數是 sigmoid 函數。 |
| 線性回歸沒有閾值。 | 在邏輯回歸中,需要一個閾值來正確確定每個實例的類別。 |
| 在線性回歸的情況下,因變量必須是連續的。 這意味著我們不能傳入變量,它是分類的並且期望在預測中具有連續值。 | 在邏輯回歸的情況下,因變量必須是分類的。 這意味著它應該有不同的類別(不超過兩個)。 |
| 該算法的目標是通過訓練數據點找到最佳擬合線。 因此,如果擬合既不超過也不低於,我們繪製的所得直線應該幾乎觸及所有訓練點。 | 如果我們對邏輯回歸曲線的係數進行任何更改,那麼它的整個圖都會改變它的形狀。 |
| 為了預測這些值,線性回歸算法做了一個基本假設。 它假設傳入該算法的值遵循標準正態分佈或按照高斯分佈分佈。 | 邏輯回歸算法還假設傳遞給 sigmoid 函數的數據的分佈。 它假設數據服從二項分佈。 |
想了解更多?
如果您有興趣了解有關機器學習的更多信息,請查看 IIIT-B 和 upGrad 的機器學習和人工智能 PG 文憑,該文憑專為工作專業人士設計,提供 450 多個小時的嚴格培訓、30 多個案例研究和作業、IIIT- B 校友身份、5 個以上實用的實踐頂點項目和頂級公司的工作協助。
使用邏輯回歸有什麼缺點?
邏輯回歸模型通過檢查一個或多個預先存在的自變量之間的聯繫來預測因數據變量。 邏輯回歸通常用於分類任務,有很多優點,但也有一些缺點。 在處理高維數據集時,可能會出現模型過擬合,導致結論不准確。 由於在採用邏輯回歸時數據準備是一個耗時的過程,因此數據維護也變得困難。 邏輯回歸的主要缺點之一是它不能處理非線性問題。
多項邏輯回歸是什麼意思?
多項邏輯回歸是一種二元邏輯回歸擴展,可以處理兩個以上的因變量或結果變量。 它類似於邏輯回歸,除了有許多可能的結果而不僅僅是一個。 它是一種具有多類分類能力的傳統監督機器學習方法。 多項邏輯模型包括各種假設,其中之一是數據被認為是特定於案例的,這意味著每個自變量對於每個實例都有一個值。 多項邏輯模型還假定,在任何給定情況下,因變量無法從自變量中精確預測。
如何使用線性回歸來解決現實生活中的問題?
線性回歸廣泛用於各種現實世界的情況和領域。 企業通常利用線性回歸來了解廣告、支出和利潤之間的關係。 醫學研究人員經常使用線性回歸來檢查藥物劑量與患者血壓之間的關聯。 農業科學家經常使用線性回歸來評估肥料和水對作物產量的影響。 因此,線性回歸在解決實際問題中的用途是多種多樣的。
