線形回帰対。 ロジスティック回帰:線形回帰とロジスティック回帰の違い
公開: 2020-09-10機械学習の世界は、最も単純な機械学習アルゴリズムが2つ存在しなければ完成しません。 はい、線形回帰とロジスティック回帰はどちらも、実装できる最も簡単な機械学習アルゴリズムです。 線形回帰とロジスティック回帰の違いについて説明する前に、まず、これら両方のアルゴリズムの基礎となる基本を理解する必要があります。
まず、これらのアルゴリズムは両方とも、本質的に教師あり学習です。 つまり、これらのアルゴリズムの両方にフィードするデータには、適切なラベルを付ける必要があります。 注意すべきもう1つの重要な点は、ユースケースです。 すぐに、これら2つのアルゴリズムの明らかな違いの1つは、両方のユースケースです。 線形回帰は、回帰を実行する場合は常に使用されます。 つまり、特定の地域の住宅価格など、連続数を予測する場合は常に線形回帰を使用します。
ただし、ロジスティック回帰の使用は分類問題で行われます。 つまり、特定の家が(価格ではなく)高価であるか安価であるかを予測する場合は、ロジスティック回帰のアルゴリズムを使用します。 はい、ロジスティック回帰の名前には回帰という単語が含まれていますが、分類に使用されます。
あなたが以下にリストされているのを見つけるそのようなエキサイティングな微妙なものがもっとあります。 ただし、線形回帰とロジスティック回帰を正面から比較する前に、まずこれらの各アルゴリズムについて詳しく見ていきましょう。
目次
線形回帰
線形回帰は、理解と展開の両方を行うための最も簡単で単純な機械学習アルゴリズムです。 これは教師あり学習アルゴリズムであるため、連続値を予測する(または回帰を実行する)場合は、適切にラベル付けされたデータセットを使用してこのアルゴリズムを提供する必要があります。 この機械学習アルゴリズムは、線形性があるため、最も簡単です。 将来の値を正しく予測するために、線形回帰は、アルゴリズムに入力されたデータを直線化しようとします。
したがって、情報が線形回帰アルゴリズムに入力されるたびに、データを取得して直線の方程式を取得し、最適な線が見つかるまで勾配と切片をランダムに選択します。 このアルゴリズムに入力するデータに独立変数が1つしかない場合、それは単純線形回帰と呼ばれます。

一方、データに複数の独立変数がある場合、回帰は重回帰になります。 線形回帰の数学的形式は、単純に直線の形式であり、以下に示されています。
y = a0 + a1x + c
ここで、yは従属変数、a0とa1はこのアルゴリズムが求める係数、xは従属変数、cはこの直線の切片値です。
ロジスティック回帰
言うまでもなく、ロジスティック回帰は、教師あり学習アルゴリズムの傘下で最も単純でありながら非常に強力な分類機械学習アルゴリズムの1つです。 このアルゴリズムは回帰問題に使用できますが、代わりに分類問題を解決するために主に使用されます。 このアルゴリズムから得られる出力は常に0から1の間であるため、しきい値分類値を使用してインスタンスをクラスに分類するのは簡単になります。

名前のロジスティックという言葉は、この回帰で使用される活性化関数を指します。 この場合、活性化関数またはロジスティック関数は、実際にはシグモイド関数に他なりません。 これは、このシグモイド関数のプロパティであり、ロジスティック回帰の値を常に0から1の間に保ちます。 シグモイド関数は次のようになります。
![]()
ここで、yはシグモイド関数による出力であり、xは独立変数です。 ロジスティック回帰の場合、変数xは実際には線形回帰方程式全体になります。 したがって、ロジスティック回帰の方程式を作成できます。これは次のように記述されます。

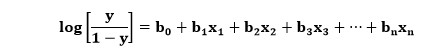
ここで、変数の意味はロジスティック回帰の意味と似ており、xは独立変数、yは従属変数、b0、b1、b2などはこのアルゴリズムが決定する係数です。
線形回帰とロジスティック回帰の違い
以下にリストされているのは、線形回帰とロジスティック回帰の包括的な比較です。
| 線形回帰 | ロジスティック回帰 |
| 十分にラベル付けされたデータが必要です。つまり、監視が必要であり、回帰に使用されます。 したがって、線形回帰は教師あり回帰アルゴリズムです。 | また、そこに供給されるデータには適切なラベルを付ける必要があります。 ただし、このアルゴリズムは回帰ではなく分類に使用されます。 したがって、ロジスティック回帰は教師あり分類アルゴリズムです。 |
| 線形回帰アルゴリズムによって得られる予測は、通常、負の無限大から正の無限大の範囲の値になります。 | ロジスティック回帰によって得られる予測は、実際には0から1の範囲にあります。 この機能により、しきい値を使用して簡単に分類できます。 |
| 線形回帰は、アクティブ化の機能を必要としません。 | ここでは、アクティベーションの機能が必要です。 この場合、その関数はシグモイド関数です。 |
| 線形回帰にはしきい値はありません。 | ロジスティック回帰では、各インスタンスのクラスを適切に決定するためにしきい値が必要です。 |
| 線形回帰の場合の従属変数は、本質的に連続でなければなりません。 つまり、変数を渡すことはできません。これはカテゴリ型であり、予測で連続値を期待します。 | ロジスティック回帰の場合の従属変数は、カテゴリ型である必要があります。 つまり、異なるカテゴリ(2つ以下)が必要です。 |
| このアルゴリズムの目標は、トレーニングデータポイントを介して最適なラインを見つけることです。 したがって、フィットが上でも下でもない場合、結果として得られる直線は、ほぼすべてのトレーニングポイントに接触するはずです。 | ロジスティック回帰曲線の係数に変更を加えると、そのプロット全体の形状が変化します。 |
| 値を予測するために、線形回帰のアルゴリズムは基本的な仮定を行います。 このアルゴリズムに渡される値は、標準正規分布に従うか、ガウス分布に従って分布していることを前提としています。 | ロジスティック回帰のアルゴリズムは、シグモイド関数に渡されるデータの分布も想定しています。 データが二項分布に従うことを前提としています。 |
もっと知りたいですか?
機械学習について詳しく知りたい場合は、IIIT-BとupGradの機械学習とAIのPGディプロマをご覧ください。これは、働く専門家向けに設計されており、450時間以上の厳格なトレーニング、30以上のケーススタディと課題、IIIT-を提供します。 B卒業生のステータス、5つ以上の実践的なキャップストーンプロジェクト、トップ企業との仕事の支援。
ロジスティック回帰を使用することの短所は何ですか?
ロジスティック回帰モデルは、1つ以上の既存の独立変数間の接続を調べることにより、従属データ変数を予測します。 分類タスクに一般的に使用されるロジスティック回帰には多くの利点がありますが、いくつかの欠点もあります。 高次元のデータセットを操作する場合、モデルの過剰適合が発生し、不正確な結論が生じる可能性があります。 ロジスティック回帰を使用する場合、データの準備は時間のかかる手順であるため、データの保守も困難になります。 ロジスティック回帰の主な欠点の1つは、非線形問題を処理できないことです。
多項ロジット回帰とはどういう意味ですか?
多項ロジスティック回帰は、3つ以上の従属変数または結果変数を処理できるバイナリロジスティック回帰拡張です。 これはロジスティック回帰に似ていますが、1つだけではなく、多くの可能な結果がある点が異なります。 これは、マルチクラス分類機能を備えた従来の教師あり機械学習アプローチです。 多項ロジットモデルにはさまざまな仮定が含まれています。その1つは、データがケース固有であると考えられていることです。つまり、各独立変数はインスタンスごとに1つの値を持ちます。 多項ロジットモデルは、どのシナリオでも、従属変数を独立変数から正確に予測することはできないと仮定しています。
線形回帰を使用して実際の問題を解決するにはどうすればよいですか?
線形回帰は、実際のさまざまな状況やセクターで広く使用されています。 企業は通常、線形回帰を利用して、広告、支出、および利益の関係を理解します。 医学研究者は、線形回帰を使用して、薬の投与量と患者の血圧との関連を調べることがよくあります。 農業科学者は、作物収量に対する肥料と水の影響を評価するために線形回帰を頻繁に採用しています。 したがって、線形回帰の使用法は、実際の問題を解決する際にさまざまです。
