Lineare Regression vs. Logistische Regression: Unterschied zwischen linearer Regression und logistischer Regression

Veröffentlicht: 2020-09-10

Die Welt des maschinellen Lernens wäre nicht vollständig ohne das Vorhandensein von zwei der einfachsten Algorithmen für maschinelles Lernen. Ja, sowohl die lineare Regression als auch die logistische Regression sind die einfachsten Algorithmen für maschinelles Lernen, die Sie implementieren können. Bevor wir auf die Unterschiede zwischen linearer und logistischer Regression eingehen, müssen wir zunächst die Grundlagen verstehen, auf denen die Grundlage dieser beiden Algorithmen gelegt wird.

Zunächst einmal sind diese beiden Algorithmen von Natur aus überwachtes Lernen. Das heißt, die Daten, die Sie in diese beiden Algorithmen eingeben, sollten gut gekennzeichnet sein. Ein weiterer wichtiger Punkt sind die Anwendungsfälle. Ein eklatanter Unterschied zwischen diesen beiden Algorithmen sind auf Anhieb die Anwendungsfälle beider Algorithmen. Die lineare Regression wird immer dann verwendet, wenn wir eine Regression durchführen möchten. Das heißt, wir verwenden die lineare Regression immer dann, wenn wir fortlaufende Zahlen vorhersagen möchten, wie z. B. die Hauspreise in einem bestimmten Gebiet.

Die Verwendung der logistischen Regression erfolgt jedoch bei Klassifizierungsproblemen. Das heißt, wenn wir vorhersagen wollen, ob ein bestimmtes Haus teuer oder billig ist (anstelle des Preises), verwenden wir den Algorithmus der logistischen Regression. Ja, obwohl die logistische Regression das Wort Regression im Namen trägt, wird sie zur Klassifizierung verwendet.

Es gibt noch mehr solcher spannender Feinheiten, die Sie unten aufgelistet finden. Aber bevor wir die lineare Regression mit der logistischen Regression direkt vergleichen, wollen wir zunächst mehr über jeden dieser Algorithmen erfahren.

Inhaltsverzeichnis

Lineare Regression

Die lineare Regression ist der einfachste und am einfachsten zu verstehende und einzusetzende Algorithmus für maschinelles Lernen. Es handelt sich um einen überwachten Lernalgorithmus. Wenn wir also die kontinuierlichen Werte vorhersagen (oder eine Regression durchführen) möchten, müssten wir diesen Algorithmus mit einem gut gekennzeichneten Datensatz versorgen. Dieser maschinelle Lernalgorithmus ist aufgrund seiner linearen Natur am einfachsten. Um zukünftige Werte erfolgreich vorherzusagen, versucht die lineare Regression, eine gerade Linie durch die in den Algorithmus eingespeisten Daten zu ziehen.

Wann immer also Informationen in einen linearen Regressionsalgorithmus eingespeist werden, nimmt er die Daten und nimmt die Gleichung einer geraden Linie, wobei er zufällig die Steigung und den Schnittpunkt auswählt, bis er die am besten passende Linie findet. Wenn die Daten, die wir in diesen Algorithmus einspeisen, nur eine einzige unabhängige Variable enthalten, spricht man von einer einfachen linearen Regression.

Wenn die Daten andererseits mehrere unabhängige Variablen enthalten, wird die Regression zu einer multiplen linearen Regression. Die mathematische Form der linearen Regression ist einfach die einer geraden Linie, die unten gezeigt wird.

y= a0+a1x+c

Hier ist y die abhängige Variable, a0 und a1 sind die Koeffizienten, die dieser Algorithmus finden soll, x ist die abhängige Variable und c ist der Schnittpunktwert dieser geraden Linie.

Logistische Regression

Es ist unnötig zu erwähnen, dass die logistische Regression einer der einfachsten, aber sehr leistungsfähigsten Klassifikationsalgorithmen für maschinelles Lernen unter dem Dach eines überwachten Lernalgorithmus ist. Dieser Algorithmus kann für Regressionsprobleme verwendet werden, wird aber hauptsächlich verwendet, um stattdessen Klassifizierungsprobleme zu lösen. Die Ausgabe, die wir von diesem Algorithmus erhalten, liegt immer zwischen 0 und 1, wodurch es mühelos wird, Instanzen mithilfe eines Schwellenwerts für die Klassifizierung in Klassen zu klassifizieren.

Das Wort Logistik im Namen bezieht sich auf die Aktivierungsfunktion, die in dieser Regression verwendet wird. Die Aktivierungsfunktion oder die logistische Funktion ist in diesem Fall eigentlich nichts anderes als die Sigmoidfunktion. Es ist die Eigenschaft dieser Sigmoidfunktion, die den Wert der logistischen Regression immer zwischen null und eins hält. Die Sigmoid-Funktion sieht etwa so aus:

Hier ist y die Ausgabe durch die Sigmoidfunktion und x die unabhängige Variable. Im Fall der logistischen Regression wäre die Variable x tatsächlich die gesamte lineare Regressionsgleichung. Daher kann die Gleichung für die logistische Regression entwickelt werden, die unten geschrieben ist:

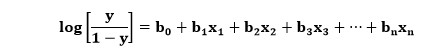
Die Bedeutung der Variablen ist hier ähnlich wie bei der logistischen Regression, x ist die unabhängige Variable und y die abhängige Variable, b0, b1, b2 usw. sind die Koeffizienten, die dieser Algorithmus bestimmt.

Unterschied zwischen linearer und logistischer Regression

Nachfolgend finden Sie einen umfassenden Vergleich der linearen Regression vs. der logistischen Regression nebeneinander:

LINEARE REGRESSION	LOGISTISCHE REGRESSION
Es erfordert gut gekennzeichnete Daten, was bedeutet, dass es überwacht werden muss, und es wird für die Regression verwendet. Somit ist die lineare Regression ein überwachter Regressionsalgorithmus.	Es erfordert auch, dass die Daten, die darin eingespeist werden, gut gekennzeichnet sind. Dieser Algorithmus wird jedoch zur Klassifizierung anstelle der Regression verwendet. Die logistische Regression ist also ein überwachter Klassifikationsalgorithmus.
Die durch den linearen Regressionsalgorithmus gewonnene Vorhersage ist normalerweise ein Wert, der im Bereich von negativ unendlich bis positiv unendlich liegen kann.	Die Vorhersage, die durch die logistische Regression gewonnen wird, liegt tatsächlich nur im Bereich von null bis eins. Diese Funktion ermöglicht eine einfache Klassifizierung mit Hilfe eines Schwellenwerts.
Die lineare Regression erfordert keine Aktivierungsfunktion.	Hier brauchen wir eine Aktivierungsfunktion. In diesem Fall ist diese Funktion die Sigmoidfunktion.
Bei der linearen Regression gibt es keinen Schwellenwert.	Bei der logistischen Regression wird ein Schwellenwert benötigt, um die Klassen jeder Instanz richtig zu bestimmen.
Die abhängige Variable im Fall einer linearen Regression muss kontinuierlicher Natur sein. Das heißt, wir können die Variable nicht übergeben, die kategorisch ist und einen kontinuierlichen Wert in der Vorhersage erwarten.	Bei der logistischen Regression muss die abhängige Variable kategorial sein. Das heißt, es sollte verschiedene Kategorien haben (nicht mehr als zwei).
Das Ziel dieses Algorithmus ist es, die Linie der besten Anpassung durch die Trainingsdatenpunkte zu finden. Somit sollte die resultierende Gerade, die wir ziehen, fast alle Trainingspunkte berühren, wenn der Fit weder über noch unter ist.	Wenn wir Änderungen am Koeffizienten der logistischen Regressionskurve vornehmen, würde der gesamte Plot davon seine Form ändern.
Für die Vorhersage der Werte trifft der Algorithmus der linearen Regression eine grundlegende Annahme. Er geht davon aus, dass die Werte, die diesem Algorithmus zugeführt werden, der Standard-Normalverteilung folgen oder gemäß der Gauß-Verteilung verteilt sind.	Der Algorithmus der logistischen Regression geht auch von der Verteilung der Daten aus, die an die Sigmoidfunktion übergeben werden. Es wird davon ausgegangen, dass die Daten der Binomialverteilung folgen.

Möchten Sie mehr erfahren?

Wenn Sie mehr über maschinelles Lernen erfahren möchten, sehen Sie sich das PG-Diplom in maschinellem Lernen und KI von IIIT-B & upGrad an, das für Berufstätige konzipiert ist und mehr als 450 Stunden strenge Schulungen, mehr als 30 Fallstudien und Aufgaben bietet, IIIT- B-Alumni-Status, mehr als 5 praktische, praktische Abschlussprojekte und Jobunterstützung bei Top-Unternehmen.

Was sind die Nachteile der Verwendung der logistischen Regression?

Ein logistisches Regressionsmodell antizipiert eine abhängige Datenvariable, indem es die Verbindung zwischen einer oder mehreren bereits bestehenden unabhängigen Variablen untersucht. Die häufig für Klassifizierungsaufgaben verwendete logistische Regression hat zahlreiche Vorteile, aber auch einige Nachteile. Bei der Arbeit mit hochdimensionalen Datensätzen kann es zu einer Überanpassung des Modells kommen, was zu ungenauen Schlussfolgerungen führt. Da die Datenvorbereitung bei der Verwendung der logistischen Regression ein zeitaufwendiges Verfahren ist, wird auch die Datenpflege schwierig. Einer der Hauptnachteile der logistischen Regression ist, dass sie nicht mit nichtlinearen Problemen umgehen kann.

Was versteht man unter multinomialer logistischer Regression?

Die multinomiale logistische Regression ist eine Erweiterung der binären logistischen Regression, die mehr als zwei abhängige oder Ergebnisvariablen verarbeiten kann. Es ähnelt der logistischen Regression, außer dass es viele mögliche Ergebnisse gibt und nicht nur eins. Es handelt sich um einen traditionellen überwachten maschinellen Lernansatz mit mehrklassigen Klassifizierungsfunktionen. Das multinomiale logistische Modell beinhaltet verschiedene Annahmen, von denen eine davon ist, dass Daten als fallspezifisch angesehen werden, was bedeutet, dass jede unabhängige Variable für jede Instanz einen einzigen Wert hat. Das multinomiale logistische Modell postuliert auch, dass in jedem gegebenen Szenario die abhängige Variable nicht genau aus den unabhängigen Variablen vorhergesagt werden kann.

Wie kann die lineare Regression verwendet werden, um reale Probleme zu lösen?

Die lineare Regression wird häufig in einer Vielzahl realer Situationen und Sektoren eingesetzt. Unternehmen verwenden in der Regel die lineare Regression, um die Beziehung zwischen Werbung, Ausgaben und Gewinn zu verstehen. Medizinische Forscher verwenden häufig die lineare Regression, um den Zusammenhang zwischen der Medikamentendosis und dem Blutdruck des Patienten zu untersuchen. Agrarwissenschaftler verwenden häufig die lineare Regression, um den Einfluss von Dünger und Wasser auf die Ernteerträge zu bewerten. Daher sind die Anwendungen der linearen Regression bei der Lösung realer Probleme vielfältig.