Doğrusal Regresyon Vs. Lojistik Regresyon: Doğrusal Regresyon ve Lojistik Regresyon Arasındaki Fark

Yayınlanan: 2020-09-10

Makine öğrenimi dünyası, en basit iki makine öğrenimi algoritmasının varlığı olmadan tamamlanmış sayılmaz. Evet, hem Doğrusal Regresyon hem de Lojistik Regresyon uygulayabileceğiniz en basit makine öğrenimi algoritmalarıdır. Doğrusal ve lojistik regresyon arasındaki farklardan herhangi birini tartışmadan önce, her iki algoritmanın da temellerinin atıldığı temelleri anlamalıyız.

İlk olarak, bu algoritmaların her ikisi de doğada denetimli öğrenmedir. Yani, bu algoritmaların her ikisine de besleyeceğiniz veriler iyi etiketlenmiş olmalıdır. Dikkat edilmesi gereken bir diğer kritik nokta da kullanım durumlarıdır. Bu iki algoritma arasındaki göze batan bir fark, her ikisinin de kullanım durumlarıdır. Doğrusal Regresyon, regresyon yapmak istediğimizde kullanılır. Yani, belirli bir bölgedeki ev fiyatları gibi sürekli sayıları tahmin etmek istediğimizde doğrusal regresyon kullanırız.

Ancak sınıflandırma problemlerinde lojistik regresyon kullanımı yapılmaktadır. Yani, belirli bir evin pahalı mı yoksa ucuz mu olduğunu (fiyat yerine) tahmin etmek istiyorsak, lojistik regresyon algoritmasını kullanırız. Evet, lojistik regresyon, adında regresyon kelimesi olmasına rağmen, sınıflandırma için kullanılır.

Aşağıda listelenmiş bulacağınız daha fazla heyecan verici incelik var. Ancak doğrusal regresyon ile lojistik regresyonu doğrudan karşılaştırmadan önce, bu algoritmaların her biri hakkında daha fazla bilgi edinelim.

İçindekiler

Doğrusal Regresyon

Doğrusal regresyon, hem anlamak hem de dağıtmak için en kolay ve en basit makine öğrenimi algoritmasıdır. Bu denetimli bir öğrenme algoritmasıdır, bu nedenle sürekli değerleri tahmin etmek (veya regresyon yapmak) istiyorsak, bu algoritmayı iyi etiketlenmiş bir veri kümesiyle sunmamız gerekir. Bu makine öğrenimi algoritması, doğrusal yapısı nedeniyle çok basittir. Gelecekteki değerleri başarılı bir şekilde tahmin etmek için doğrusal regresyon, algoritmaya beslenen veriler boyunca düz bir çizgiye ulaşmaya çalışır.

Bu nedenle, herhangi bir bilgi bir lineer regresyon algoritmasına beslendiğinde, verileri alır ve düz bir çizginin denklemini alır, eğimi rastgele seçer ve en uygun çizgiyi bulana kadar kesişir. Bu algoritmaya beslediğimiz veriler yalnızca tek bir bağımsız değişken içeriyorsa, buna basit doğrusal regresyon denir.

Öte yandan, verilerin birden fazla bağımsız değişkeni varsa, regresyon çoklu doğrusal bir regresyon haline gelir. Doğrusal regresyonun matematiksel biçimi, aşağıda gösterilen düz bir çizginin biçimidir.

y= a0+a1x+ c

Burada y bağımlı değişken, a0 ve a1 bu algoritmanın bulması gereken katsayı, x bağımlı değişken ve c bu doğrunun kesişme değeridir.

Lojistik regresyon

Lojistik regresyonun, denetimli öğrenme algoritması çatısı altında en basit ancak çok güçlü sınıflandırma makine öğrenmesi algoritmalarından biri olduğunu söylemeye gerek yok. Bu algoritma regresyon problemleri için kullanılabilir, ancak bunun yerine daha çok sınıflandırma problemlerini çözmek için kullanılır. Bu algoritmadan elde ettiğimiz çıktı her zaman 0 ile 1 arasındadır, bu nedenle örnekleri bir eşik sınıflandırma değeri kullanarak sınıflara ayırmak zahmetsiz hale gelir.

Adındaki lojistik kelimesi bu regresyonda kullanılan aktivasyon fonksiyonunu ifade etmektedir. Aktivasyon fonksiyonu veya lojistik fonksiyon, bu durumda, aslında sigmoid fonksiyonundan başka bir şey değildir. Lojistik regresyonun değerini her zaman sıfır ile bir arasında tutan bu sigmoid fonksiyonunun özelliğidir. sigmoid işlevi şuna benzer:

Burada y, sigmoid işlevi aracılığıyla çıktıdır ve x, bağımsız değişkendir. Lojistik regresyon durumunda, x değişkeni aslında tüm lineer regresyon denklemi olacaktır. Bu nedenle, aşağıda yazılan lojistik regresyon denklemi geliştirilebilir:

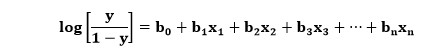
Burada değişkenlerin anlamı lojistik regresyondakine benzerdir, x bağımsız değişkendir ve y bağımlı değişkendir, b0, b1, b2 vb. bu algoritmanın belirlediği katsayılardır.

Doğrusal ve lojistik regresyon arasındaki fark

Aşağıda listelenen, doğrusal regresyon ile lojistik regresyonun yan yana kapsamlı bir karşılaştırmasını bulacaksınız:

LİNEER REGRESYON	LOJİSTİK REGRESYON
İyi etiketlenmiş verilere ihtiyaç duyar, yani denetime ihtiyaç duyar ve regresyon için kullanılır. Bu nedenle, doğrusal regresyon, denetimli bir regresyon algoritmasıdır.	Ayrıca, içine beslenen verilerin iyi etiketlenmesini gerektirir. Ancak bu algoritma regresyon yerine sınıflandırma için kullanılmaktadır. Dolayısıyla lojistik regresyon, denetimli bir sınıflandırma algoritmasıdır.
Doğrusal regresyon algoritması yoluyla elde edilen tahmin, genellikle negatif sonsuz ile pozitif sonsuz aralığında olabilen bir değerdir.	Lojistik regresyon yoluyla elde edilen tahmin aslında sadece sıfıra bir aralığındadır. Bu özellik, bir eşik değeri yardımıyla kolay bir sınıflandırma yapılmasına olanak sağlar.
Doğrusal regresyon, aktivasyon işlevi gerektirmez.	Burada bir aktivasyon fonksiyonuna ihtiyacımız var. Bu durumda, bu işlev sigmoid işlevidir.
Doğrusal regresyonda eşik değeri yoktur.	Lojistik regresyonda, her bir örneğin sınıflarını doğru bir şekilde belirlemek için bir eşik değerine ihtiyaç vardır.
Doğrusal regresyon durumunda bağımlı değişken, doğası gereği sürekli olmalıdır. Yani kategorik olan ve tahminde sürekli değer bekleyen değişkeni geçemeyiz.	Lojistik regresyon durumunda bağımlı değişken kategorik olmalıdır. Yani farklı kategorilere sahip olmalıdır (ikiden fazla değil).
Bu algoritmanın amacı, eğitim veri noktaları aracılığıyla en uygun çizgiyi bulmaktır. Bu nedenle, çizdiğimiz sonuçtaki düz çizgi, uyum ne üstte ne de altta ise hemen hemen tüm eğitim noktalarına değmelidir.	Lojistik regresyon eğrisinin katsayısında herhangi bir değişiklik yaparsak, grafiğin tamamı şeklini değiştirir.
Değerleri tahmin etmek için doğrusal regresyon algoritması temel bir varsayımda bulunur. Bu algoritmaya iletilen değerlerin standart normal dağılımı takip ettiğini veya gauss dağılımına göre dağıtıldığını varsayar.	Lojistik regresyon algoritması aynı zamanda sigmoid işlevine iletilen verilerin dağılımına ilişkin bir varsayımda bulunur. Verilerin binom dağılımını takip ettiğini varsayar.

Daha fazla öğrenmek ister misiniz?

Makine öğrenimi hakkında daha fazla bilgi edinmek istiyorsanız, çalışan profesyoneller için tasarlanmış ve 450+ saat zorlu eğitim, 30'dan fazla vaka çalışması ve ödev, IIIT- sunan IIIT-B & upGrad'ın Makine Öğrenimi ve Yapay Zeka PG Diplomasına göz atın. B Mezun statüsü, 5+ pratik uygulamalı bitirme projesi ve en iyi firmalarla iş yardımı.

Lojistik regresyon kullanmanın eksileri nelerdir?

Lojistik regresyon modeli, önceden var olan bir veya daha fazla bağımsız değişken arasındaki bağlantıyı inceleyerek bağımlı bir veri değişkenini tahmin eder. Sınıflandırma görevleri için yaygın olarak kullanılan lojistik regresyon, birçok avantaja sahip olmakla birlikte bazı dezavantajlara da sahiptir. Yüksek boyutlu veri kümeleri ile çalışırken, modelin fazla uydurması meydana gelebilir ve bu da hatalı sonuçlara neden olabilir. Lojistik regresyon kullanılırken veri hazırlama zaman alıcı bir prosedür olduğundan, veri bakımı da zorlaşır. Lojistik regresyonun en büyük dezavantajlarından biri, doğrusal olmayan problemlerle başa çıkamamasıdır.

Çok terimli lojistik regresyon ile ne kastedilmektedir?

Çok terimli lojistik regresyon, ikiden fazla bağımlı veya sonuç değişkenini işleyebilen bir ikili lojistik regresyon uzantısıdır. Lojistik regresyona benzer, ancak tek bir sonuç yerine birçok olası sonuç vardır. Çok sınıflı sınıflandırma yeteneklerine sahip geleneksel bir denetimli makine öğrenimi yaklaşımıdır. Çok terimli lojistik model, çeşitli varsayımlar içerir; bunlardan biri, verilerin duruma özel olduğu düşünülür, yani her bağımsız değişken her örnek için tek bir değere sahiptir. Çok terimli lojistik model ayrıca, herhangi bir belirli senaryoda, bağımlı değişkenin bağımsız değişkenlerden tam olarak tahmin edilemeyeceğini de varsayar.

Gerçek hayat problemlerini çözmek için lineer regresyon nasıl kullanılabilir?

Doğrusal regresyon, çeşitli gerçek dünya durumlarında ve sektörlerde yaygın olarak kullanılmaktadır. İşletmeler genellikle reklam, harcama ve kâr arasındaki ilişkiyi anlamak için doğrusal regresyon kullanır. Tıp araştırmacıları, ilaç dozu ile hastanın kan basıncı arasındaki ilişkiyi incelemek için sıklıkla lineer regresyon kullanır. Tarım bilimciler, gübre ve suyun mahsul verimi üzerindeki etkisini değerlendirmek için sıklıkla doğrusal regresyon kullanır. Bu nedenle, gerçek hayat problemlerinin çözümünde lineer regresyonun kullanımları çeşitlidir.