Regresi Linier Vs. Regresi Logistik: Perbedaan Antara Regresi Linier & Regresi Logistik

Diterbitkan: 2020-09-10

Dunia pembelajaran mesin tidak akan lengkap tanpa kehadiran dua algoritma pembelajaran mesin yang paling sederhana. Ya, Regresi Linier dan Regresi Logistik adalah algoritme pembelajaran mesin paling mudah yang dapat Anda terapkan. Sebelum membahas salah satu perbedaan antara regresi linier dan logistik, pertama-tama kita harus memahami dasar-dasar di mana kedua algoritma ini diletakkan.

Pertama, kedua algoritma ini adalah pembelajaran yang diawasi secara alami. Artinya, data yang akan Anda masukkan ke dalam kedua algoritme ini harus diberi label dengan baik. Hal penting lainnya yang perlu diperhatikan adalah kasus penggunaan. Langsung saja, satu perbedaan mencolok antara kedua algoritma ini adalah kasus penggunaan keduanya. Regresi Linier digunakan setiap kali kita ingin melakukan regresi. Artinya, kami menggunakan regresi linier setiap kali kami ingin memprediksi angka yang berkelanjutan, seperti harga rumah di area tertentu.

Namun, penggunaan regresi logistik dilakukan dalam masalah klasifikasi. Artinya, jika kita ingin memprediksi apakah rumah tertentu mahal atau murah (bukan harganya), kita menggunakan algoritma regresi logistik. Ya, meskipun regresi logistik memiliki kata regresi dalam namanya, itu digunakan untuk klasifikasi.

Ada lebih banyak seluk-beluk menarik yang akan Anda temukan tercantum di bawah ini. Namun sebelum membandingkan regresi linier vs. regresi logistik secara langsung, mari kita pelajari lebih lanjut tentang masing-masing algoritme ini.

Daftar isi

Regresi linier

Regresi linier adalah algoritme pembelajaran mesin yang paling mudah dan sederhana untuk dipahami dan diterapkan. Ini adalah algoritma pembelajaran yang diawasi, jadi jika kita ingin memprediksi nilai kontinu (atau melakukan regresi), kita harus menyajikan algoritma ini dengan kumpulan data yang diberi label dengan baik. Algoritma pembelajaran mesin ini paling mudah karena sifatnya yang linier. Untuk berhasil memprediksi nilai masa depan, regresi linier mencoba membuat garis lurus melalui data yang dimasukkan ke dalam algoritma.

Jadi, setiap kali informasi apa pun dimasukkan ke dalam algoritma regresi linier, itu mengambil data dan mengambil persamaan garis lurus, secara acak memilih kemiringan dan mencegat sampai menemukan garis yang paling cocok. Jika data yang kita masukkan ke dalam algoritma ini hanya berisi satu variabel bebas, maka disebut regresi linier sederhana.

Sebaliknya, jika data memiliki beberapa variabel bebas, maka regresi tersebut menjadi regresi linier berganda. Bentuk matematis dari regresi linier hanyalah berupa garis lurus, yang ditunjukkan di bawah ini.

y= a0+a1x+ c

Di sini, y adalah variabel dependen, a0 dan a1 adalah koefisien yang harus dicari oleh algoritma ini, x adalah variabel dependen, dan c adalah nilai intersep dari garis lurus ini.

Regresi logistik

Tidak perlu dikatakan bahwa regresi logistik adalah salah satu algoritma pembelajaran mesin klasifikasi yang paling mudah namun sangat kuat di bawah payung algoritma pembelajaran yang diawasi. Algoritma ini dapat digunakan untuk masalah regresi, tetapi sebagian besar digunakan untuk menyelesaikan masalah klasifikasi. Output yang kami dapatkan dari algoritma ini selalu antara 0 dan 1 sehingga menjadi mudah untuk mengklasifikasikan instance ke dalam kelas dengan menggunakan nilai klasifikasi ambang batas.

Kata logistik dalam nama mengacu pada fungsi aktivasi, yang digunakan dalam regresi ini. Fungsi aktivasi atau fungsi logistik dalam hal ini sebenarnya tidak lain adalah fungsi sigmoid. Ini adalah properti dari fungsi sigmoid ini, yang menjaga nilai regresi logistik selalu antara nol dan satu. Fungsi sigmoid terlihat seperti ini:

Di sini, y adalah output melalui fungsi sigmoid, dan x adalah variabel independen. Dalam kasus regresi logistik, variabel x sebenarnya adalah seluruh persamaan regresi linier. Oleh karena itu, persamaan untuk regresi logistik dapat dikembangkan, yang ditulis di bawah ini:

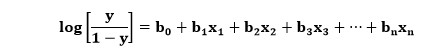
Di sini, arti dari variabel mirip dengan yang ada di regresi logistik, x adalah variabel independen, dan y adalah variabel dependen, b0, b1, b2, dll, adalah koefisien yang ditentukan oleh algoritma ini.

Perbedaan antara regresi linier dan logistik

Di bawah ini, Anda akan menemukan perbandingan komprehensif regresi linier vs. regresi logistik secara berdampingan:

REGRESI LINIER	REGRESI LOGISTIK
Ini membutuhkan data berlabel baik yang berarti perlu pengawasan, dan digunakan untuk regresi. Dengan demikian, regresi linier adalah algoritma regresi terawasi.	Ini juga membutuhkan data yang dimasukkan ke dalamnya untuk diberi label dengan baik. Namun, algoritma ini digunakan untuk klasifikasi bukan regresi. Jadi regresi logistik adalah algoritma klasifikasi terawasi.
Prediksi yang diperoleh melalui algoritma regresi linier biasanya berupa nilai yang dapat berada dalam kisaran tak terhingga negatif hingga tak terhingga positif.	Prediksi yang diperoleh melalui regresi logistik sebenarnya berada pada kisaran nol sampai satu saja. Fitur ini memungkinkan klasifikasi yang mudah dengan bantuan nilai ambang batas.
Regresi linier tidak memerlukan fungsi aktivasi.	Di sini kita membutuhkan fungsi aktivasi. Dalam hal ini, fungsi tersebut adalah fungsi sigmoid.
Tidak ada nilai ambang batas dalam regresi linier.	Dalam regresi logistik, nilai ambang batas diperlukan untuk menentukan kelas setiap instance dengan benar.
Variabel terikat dalam kasus regresi linier harus bersifat kontinu. Artinya kita tidak bisa melewatkan variabel yang bersifat kategoris dan mengharapkan nilai yang kontinu dalam prediksi.	Variabel terikat dalam kasus regresi logistik harus kategoris. Artinya harus memiliki kategori yang berbeda (tidak lebih dari dua).
Tujuan dari algoritma ini adalah untuk menemukan garis yang paling cocok melalui titik-titik data pelatihan. Jadi, garis lurus yang dihasilkan, yang kita gambar, harus menyentuh hampir semua titik latihan jika kecocokannya tidak di atas atau di bawah.	Jika kita membuat perubahan pada koefisien kurva regresi logistik, maka seluruh plotnya akan berubah bentuknya.
Untuk memprediksi nilai, algoritma regresi linier membuat asumsi mendasar. Diasumsikan bahwa nilai-nilai yang dilewatkan ke dalam algoritma ini mengikuti distribusi normal standar atau terdistribusi sesuai dengan distribusi gaussian.	Algoritma regresi logistik juga membuat asumsi distribusi data yang dilewatkan ke dalam fungsi sigmoid. Diasumsikan bahwa data mengikuti distribusi binomial.

Ingin belajar lebih banyak?

Jika Anda tertarik untuk mempelajari lebih lanjut tentang pembelajaran mesin, lihat PG Diploma IIIT-B & upGrad dalam Pembelajaran Mesin & AI yang dirancang untuk para profesional yang bekerja dan menawarkan 450+ jam pelatihan ketat, 30+ studi kasus & tugas, IIIT- B Status alumni, 5+ proyek batu penjuru praktis & bantuan pekerjaan dengan perusahaan-perusahaan top.

Apa kontra menggunakan regresi logistik?

Sebuah model regresi logistik mengantisipasi variabel data dependen dengan memeriksa hubungan antara satu atau lebih variabel independen yang sudah ada sebelumnya. Regresi logistik, yang biasa digunakan untuk tugas klasifikasi, memiliki banyak keuntungan, tetapi juga memiliki beberapa kelemahan. Saat bekerja dengan kumpulan data berdimensi tinggi, model yang terlalu pas dapat terjadi, sehingga menghasilkan kesimpulan yang tidak akurat. Karena persiapan data adalah prosedur yang memakan waktu saat menggunakan regresi logistik, pemeliharaan data juga menjadi sulit. Salah satu kelemahan utama dari regresi logistik adalah tidak dapat menangani masalah non-linier.

Apa yang dimaksud dengan regresi logistik multinomial?

Regresi logistik multinomial adalah ekstensi regresi logistik biner yang dapat menangani lebih dari dua variabel dependen atau hasil. Ini mirip dengan regresi logistik, kecuali bahwa ada banyak kemungkinan hasil daripada hanya satu. Ini adalah pendekatan pembelajaran mesin terawasi tradisional dengan kemampuan klasifikasi multi-kelas. Model logistik multinomial mencakup berbagai asumsi, salah satunya adalah bahwa data dianggap case-specific, artinya setiap variabel independen memiliki nilai tunggal untuk setiap instance. Model logistik multinomial juga menyatakan bahwa dalam skenario tertentu, variabel dependen tidak dapat diprediksi secara tepat dari variabel independen.

Bagaimana regresi linier dapat digunakan untuk memecahkan masalah kehidupan nyata?

Regresi linier banyak digunakan dalam berbagai situasi dan sektor dunia nyata. Bisnis biasanya menggunakan regresi linier untuk memahami hubungan antara iklan, pengeluaran, dan laba. Peneliti medis sering menggunakan regresi linier untuk menguji hubungan antara dosis obat dan tekanan darah pasien. Ilmuwan pertanian sering menggunakan regresi linier untuk menilai pengaruh pupuk dan air pada hasil panen. Dengan demikian, penggunaan regresi linier bervariasi dalam memecahkan masalah kehidupan nyata.