Regressão linear vs. Regressão Logística: Diferença entre Regressão Linear e Regressão Logística

Publicados: 2020-09-10

O mundo do aprendizado de máquina não estaria completo sem a presença de dois dos algoritmos de aprendizado de máquina mais simples. Sim, tanto a regressão linear quanto a regressão logística são os algoritmos de aprendizado de máquina mais simples que você pode implementar. Antes de discutir qualquer uma das diferenças entre regressão linear e logística, devemos primeiro entender os fundamentos sobre os quais os fundamentos de ambos os algoritmos são estabelecidos.

Primeiro, ambos os algoritmos são de aprendizado supervisionado por natureza. Ou seja, os dados que você alimentará em ambos os algoritmos devem ser bem rotulados. Outra coisa importante a ser observada são os casos de uso. Logo de cara, uma diferença gritante entre esses dois algoritmos são os casos de uso de ambos. A Regressão Linear é usada sempre que desejamos realizar uma regressão. Ou seja, usamos regressão linear sempre que queremos prever números contínuos, como os preços das casas em uma determinada área.

No entanto, o uso da regressão logística é feito em problemas de classificação. Ou seja, se queremos prever se uma determinada casa é cara ou barata (em vez do preço), usamos o algoritmo de regressão logística. Sim, embora a regressão logística tenha a palavra regressão em seu nome, ela é usada para classificação.

Existem mais sutilezas emocionantes que você encontrará listadas abaixo. Mas antes de comparar a regressão linear com a regressão logística de frente, vamos primeiro aprender mais sobre cada um desses algoritmos.

Índice

Regressão linear

A regressão linear é o algoritmo de aprendizado de máquina mais fácil e simples de entender e implantar. É um algoritmo de aprendizado supervisionado, portanto, se quisermos prever os valores contínuos (ou realizar regressão), teríamos que servir a esse algoritmo com um conjunto de dados bem rotulado. Esse algoritmo de aprendizado de máquina é mais direto devido à sua natureza linear. Para prever com sucesso valores futuros, a regressão linear tenta uma linha reta através dos dados alimentados no algoritmo.

Assim, sempre que alguma informação é alimentada em um algoritmo de regressão linear, ele pega os dados e pega a equação de uma linha reta, selecionando aleatoriamente a inclinação e a interceptação até encontrar a linha de melhor ajuste. Se os dados que alimentamos nesse algoritmo contiverem apenas uma única variável independente, ela será chamada de regressão linear simples.

Por outro lado, se os dados tiverem múltiplas variáveis independentes, então a regressão se torna uma regressão linear múltipla. A forma matemática da regressão linear é simplesmente a de uma linha reta, que é mostrada abaixo.

y= a0+a1x+ c

Aqui, y é a variável dependente, a0 e a1 é o coeficiente que esse algoritmo tem a tarefa de encontrar, x é a variável dependente e c é o valor de interceptação dessa linha reta.

Regressão Logística

É desnecessário dizer que a regressão logística é um dos algoritmos de aprendizado de máquina de classificação mais diretos, porém muito poderosos, sob o guarda-chuva de um algoritmo de aprendizado supervisionado. Esse algoritmo pode ser usado para problemas de regressão, mas é usado principalmente para resolver problemas de classificação. A saída que obtemos desse algoritmo está sempre entre 0 e 1, devido ao qual se torna fácil classificar instâncias em classes usando um valor de classificação de limite.

A palavra logística no nome refere-se à função de ativação, que é usada nesta regressão. A função de ativação ou função logística, neste caso, na verdade nada mais é do que a função sigmóide. É propriedade desta função sigmóide, que mantém o valor da regressão logística sempre entre zero e um. A função sigmoid se parece com isso:

Aqui, y é a saída através da função sigmóide e x é a variável independente. No caso da regressão logística, a variável x seria na verdade toda a equação de regressão linear. Assim, a equação para a regressão logística pode ser desenvolvida, que está escrita abaixo:

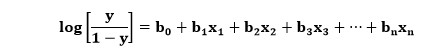
Aqui, o significado das variáveis é semelhante ao da regressão logística, x é a variável independente e y é a variável dependente, b0, b1, b2, etc., são o coeficiente que este algoritmo determina.

Diferença entre regressão linear e logística

Listado abaixo, você encontrará uma comparação abrangente de regressão linear versus regressão logística lado a lado:

REGRESSÃO LINEAR	REGRESSÃO LOGÍSTICA
Requer dados bem rotulados, o que significa que precisa de supervisão, e é usado para regressão. Assim, a regressão linear é um algoritmo de regressão supervisionado.	Também requer que os dados que são inseridos nele sejam bem rotulados. No entanto, esse algoritmo é usado para classificação em vez de regressão. Portanto, a regressão logística é um algoritmo de classificação supervisionado.
A previsão obtida por meio do algoritmo de regressão linear geralmente é um valor que pode estar na faixa de infinito negativo a infinito positivo.	A previsão obtida por meio da regressão logística está, na verdade, na faixa de apenas zero a um. Este recurso permite uma classificação fácil com a ajuda de um valor limite.
A regressão linear não requer função de ativação.	Aqui precisamos de uma função de ativação. Neste caso, essa função é a função sigmóide.
Não há valor limite na regressão linear.	Na regressão logística, é necessário um valor limite para determinar adequadamente as classes de cada instância.
A variável dependente no caso de regressão linear tem que ser de natureza contínua. Ou seja, não podemos passar a variável, que é categórica e esperar um valor contínuo na previsão.	A variável dependente no caso de regressão logística tem que ser categórica. Ou seja, deve ter categorias diferentes (não mais que duas).
O objetivo deste algoritmo é encontrar a linha de melhor ajuste através dos pontos de dados de treinamento. Assim, a linha reta resultante, que traçamos, deve tocar quase todos os pontos de treinamento se o ajuste não for nem acima nem abaixo.	Se fizermos qualquer alteração no coeficiente da curva de regressão logística, todo o gráfico dela mudará de forma.
Para prever os valores, o algoritmo de regressão linear faz uma suposição fundamental. Assume-se que os valores que são passados para este algoritmo seguem a distribuição normal padrão ou são distribuídos de acordo com a distribuição gaussiana.	O algoritmo de regressão logística também supõe a distribuição dos dados que estão sendo passados para a função sigmóide. Assume-se que os dados seguem a distribuição binomial.

Quer aprender mais?

Se você estiver interessado em aprender mais sobre aprendizado de máquina, confira o PG Diploma in Machine Learning & AI do IIIT-B e upGrad, projetado para profissionais que trabalham e oferece mais de 450 horas de treinamento rigoroso, mais de 30 estudos de caso e atribuições, IIIT- B Status de ex-aluno, mais de 5 projetos práticos práticos e assistência de trabalho com as principais empresas.

Quais são os contras de usar a regressão logística?

Um modelo de regressão logística antecipa uma variável de dados dependente examinando a conexão entre uma ou mais variáveis independentes pré-existentes. A regressão logística, que é comumente usada para tarefas de classificação, tem inúmeras vantagens, mas também apresenta algumas desvantagens. Ao trabalhar com conjuntos de dados de alta dimensão, pode ocorrer overfitting do modelo, resultando em conclusões imprecisas. Como a preparação de dados é um procedimento demorado ao empregar a regressão logística, a manutenção dos dados também se torna difícil. Uma das principais desvantagens da regressão logística é que ela não pode lidar com problemas não lineares.

O que significa regressão logística multinomial?

A regressão logística multinomial é uma extensão de regressão logística binária que pode lidar com mais de duas variáveis dependentes ou de resultado. É semelhante à regressão logística, exceto que há muitos resultados possíveis em vez de apenas um. É uma abordagem tradicional de aprendizado de máquina supervisionado com recursos de classificação multiclasse. O modelo logístico multinomial inclui várias suposições, uma das quais é que os dados são considerados específicos do caso, o que significa que cada variável independente tem um valor único para cada instância. O modelo logístico multinomial também postula que, em qualquer cenário, a variável dependente não pode ser predita com precisão a partir das variáveis independentes.

Como a regressão linear pode ser usada para resolver problemas da vida real?

A regressão linear é amplamente utilizada em uma variedade de situações e setores do mundo real. As empresas normalmente utilizam a regressão linear para entender a relação entre publicidade, gastos e lucro. Pesquisadores médicos freqüentemente empregam regressão linear para examinar a associação entre a dose do medicamento e a pressão arterial do paciente. Cientistas agrícolas freqüentemente empregam regressão linear para avaliar a influência de fertilizantes e água no rendimento das culturas. Assim, os usos da regressão linear são variados na resolução de problemas da vida real.