Линейная регрессия против. Логистическая регрессия: разница между линейной регрессией и логистической регрессией
Опубликовано: 2020-09-10Мир машинного обучения был бы неполным без наличия двух простейших алгоритмов машинного обучения. Да, и линейная регрессия, и логистическая регрессия — самые простые алгоритмы машинного обучения, которые вы можете реализовать. Прежде чем обсуждать какие-либо различия между линейной и логистической регрессией, мы должны сначала понять основы, на которых заложена основа обоих этих алгоритмов.
Во-первых, оба этих алгоритма по своей природе являются контролируемым обучением. Это означает, что данные, которые вы будете вводить в оба этих алгоритма, должны быть хорошо помечены. Еще одна важная вещь, на которую следует обратить внимание, — это варианты использования. Сразу же бросается в глаза одно очевидное различие между этими двумя алгоритмами — варианты использования обоих. Линейная регрессия используется всякий раз, когда мы хотим выполнить регрессию. Это означает, что мы используем линейную регрессию всякий раз, когда хотим предсказать непрерывные числа, например, цены на жилье в определенном районе.
Однако использование логистической регрессии выполняется в задачах классификации. Это означает, что если мы хотим предсказать, дорогой или недорогой конкретный дом (вместо цены), мы используем алгоритм логистической регрессии. Да, несмотря на то, что в названии логистической регрессии есть слово «регрессия», оно используется для классификации.
Есть еще такие волнующие тонкости, которые вы найдете ниже. Но прежде чем сравнивать линейную регрессию с логистической регрессией, давайте сначала узнаем больше о каждом из этих алгоритмов.
Оглавление
Линейная регрессия
Линейная регрессия — это самый простой алгоритм машинного обучения как для понимания, так и для развертывания. Это алгоритм обучения с учителем, поэтому, если мы хотим предсказать непрерывные значения (или выполнить регрессию), нам придется обслуживать этот алгоритм с хорошо размеченным набором данных. Этот алгоритм машинного обучения наиболее прост из-за его линейной природы. Чтобы успешно предсказать будущие значения, линейная регрессия пытается провести прямую линию через данные, подаваемые в алгоритм.
Таким образом, всякий раз, когда какая-либо информация подается в алгоритм линейной регрессии, он берет данные и принимает уравнение прямой линии, случайным образом выбирая наклон и точку пересечения, пока не найдет линию наилучшего соответствия. Если данные, которые мы вводим в этот алгоритм, содержат только одну независимую переменную, то это называется простой линейной регрессией.

С другой стороны, если данные имеют несколько независимых переменных, регрессия становится множественной линейной регрессией. Математическая форма линейной регрессии — это просто прямая линия, показанная ниже.
у= а0+а1х+с
Здесь y — зависимая переменная, a0 и a1 — коэффициенты, которые должен найти этот алгоритм, x — зависимая переменная, а c — значение точки пересечения этой прямой.
Логистическая регрессия
Излишне говорить, что логистическая регрессия является одним из самых простых, но очень мощных алгоритмов машинного обучения классификации под эгидой алгоритма обучения с учителем. Этот алгоритм можно использовать для задач регрессии, но в основном он используется для решения задач классификации. Результат, который мы получаем от этого алгоритма, всегда находится между 0 и 1, благодаря чему становится легко классифицировать экземпляры по классам, используя пороговое значение классификации.

Слово логистика в названии относится к функции активации, которая используется в этой регрессии. Функция активации или логистическая функция в данном случае на самом деле не что иное, как сигмовидная функция. Это свойство этой сигмовидной функции, которое всегда удерживает значение логистической регрессии между нулем и единицей. Сигмовидная функция выглядит примерно так:
![]()
Здесь y — результат сигмовидной функции, а x — независимая переменная. В случае логистической регрессии переменная x на самом деле будет всем уравнением линейной регрессии. Следовательно, можно составить уравнение логистической регрессии, которое написано ниже:
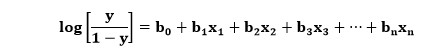
Здесь значения переменных аналогичны значениям в логистической регрессии, x — независимая переменная, y — зависимая переменная, b0, b1, b2 и т. д. — коэффициенты, которые определяет этот алгоритм.

Разница между линейной и логистической регрессией
В приведенном ниже списке вы найдете всестороннее сравнение линейной регрессии и логистической регрессии:
| ЛИНЕЙНАЯ РЕГРЕССИЯ | ЛОГИСТИЧЕСКАЯ РЕГРЕССИЯ |
| Для этого требуются хорошо помеченные данные, что означает, что он нуждается в наблюдении, и он используется для регрессии. Таким образом, линейная регрессия представляет собой алгоритм регрессии с учителем. | Он также требует, чтобы данные, которые вводятся в него, были хорошо помечены. Однако этот алгоритм используется для классификации вместо регрессии. Таким образом, логистическая регрессия — это контролируемый алгоритм классификации. |
| Прогноз, полученный с помощью алгоритма линейной регрессии, обычно представляет собой значение, которое может находиться в диапазоне от отрицательной бесконечности до положительной бесконечности. | Прогноз, полученный с помощью логистической регрессии, на самом деле находится в диапазоне от нуля до единицы. Эта функция позволяет легко классифицировать с помощью порогового значения. |
| Линейная регрессия не требует функции активации. | Здесь нам понадобится функция активации. В данном случае эта функция является сигмовидной. |
| В линейной регрессии нет порогового значения. | В логистической регрессии пороговое значение необходимо для правильного определения классов каждого экземпляра. |
| Зависимая переменная в случае линейной регрессии должна быть непрерывной по своей природе. Это означает, что мы не можем передать переменную, которая является категориальной, и ожидать непрерывного значения в прогнозе. | Зависимая переменная в случае логистической регрессии должна быть категориальной. То есть он должен иметь разные категории (не более двух). |
| Цель этого алгоритма — найти линию наилучшего соответствия через точки обучающих данных. Таким образом, результирующая прямая, которую мы проводим, должна касаться почти всех тренировочных точек, если посадка не будет ни сверху, ни снизу. | Если мы внесем какие-либо изменения в коэффициент кривой логистической регрессии, то весь ее график изменит свою форму. |
| Для прогнозирования значений алгоритм линейной регрессии делает фундаментальное предположение. Предполагается, что значения, которые передаются в этот алгоритм, следуют стандартному нормальному распределению или распределяются в соответствии с распределением Гаусса. | Алгоритм логистической регрессии также делает предположение о распределении данных, которые передаются в сигмовидную функцию. Предполагается, что данные следуют биномиальному распределению. |
Хотите узнать больше?
Если вам интересно узнать больше о машинном обучении, ознакомьтесь с дипломом PG IIIT-B и upGrad в области машинного обучения и искусственного интеллекта, который предназначен для работающих профессионалов и предлагает более 450 часов тщательного обучения, более 30 тематических исследований и заданий, IIIT- Статус B Alumni, более 5 практических практических проектов и помощь в трудоустройстве в ведущих фирмах.
Каковы недостатки использования логистической регрессии?
Модель логистической регрессии предвосхищает зависимую переменную данных, исследуя связь между одной или несколькими ранее существовавшими независимыми переменными. Логистическая регрессия, которая обычно используется для задач классификации, имеет множество преимуществ, но также имеет и некоторые недостатки. При работе с многомерными наборами данных может произойти переобучение модели, что приведет к неточным выводам. Поскольку подготовка данных при использовании логистической регрессии требует много времени, обслуживание данных также усложняется. Один из основных недостатков логистической регрессии заключается в том, что она не может решать нелинейные задачи.
Что понимается под полиномиальной логистической регрессией?
Полиномиальная логистическая регрессия — это расширение бинарной логистической регрессии, которое может обрабатывать более двух зависимых или конечных переменных. Это похоже на логистическую регрессию, за исключением того, что существует множество возможных результатов, а не один. Это традиционный подход к контролируемому машинному обучению с возможностями многоклассовой классификации. Полиномиальная логистическая модель включает в себя различные допущения, одно из которых заключается в том, что данные считаются специфическими для конкретного случая, а это означает, что каждая независимая переменная имеет единственное значение для каждого случая. Полиномиальная логистическая модель также утверждает, что в любом заданном сценарии зависимая переменная не может быть точно предсказана на основе независимых переменных.
Как можно использовать линейную регрессию для решения реальных задач?
Линейная регрессия широко используется в различных реальных ситуациях и секторах. Компании обычно используют линейную регрессию, чтобы понять взаимосвязь между рекламой, расходами и прибылью. Медицинские исследователи часто используют линейную регрессию для изучения связи между дозой лекарства и кровяным давлением пациента. Ученые-агрономы часто используют линейную регрессию для оценки влияния удобрений и воды на урожайность. Таким образом, использование линейной регрессии разнообразно при решении реальных задач.
