线性回归与。 逻辑回归:线性回归和逻辑回归之间的区别
已发表: 2020-09-10如果没有两种最简单的机器学习算法,机器学习的世界将是不完整的。 是的,线性回归和逻辑回归都是您可以实现的最直接的机器学习算法。 在讨论线性回归和逻辑回归之间的任何区别之前,我们必须首先了解这两种算法的基础。
首先,这两种算法本质上都是监督学习。 这意味着,您将提供给这两种算法的数据应该被很好地标记。 另一个需要注意的关键是用例。 马上,这两种算法之间的一个明显区别是两者的用例。 每当我们想要执行回归时,都会使用线性回归。 这意味着,每当我们想要预测连续数字时,我们都会使用线性回归,例如特定区域的房价。
但是,逻辑回归的使用是在分类问题中完成的。 这意味着,如果我们想预测特定房子是昂贵还是便宜(而不是价格),我们使用逻辑回归算法。 是的,即使逻辑回归的名称中有回归这个词,它也用于分类。
您将在下面找到更多这样令人兴奋的微妙之处。 但在正面比较线性回归与逻辑回归之前,让我们首先了解有关这些算法的更多信息。
目录
线性回归
线性回归是最容易理解和部署的机器学习算法。 它是一种监督学习算法,因此如果我们想要预测连续值(或执行回归),我们必须使用标记良好的数据集为该算法提供服务。 这种机器学习算法是最直接的,因为它具有线性特性。 为了成功预测未来值,线性回归尝试通过输入算法的数据形成一条直线。
因此,每当将任何信息输入线性回归算法时,它都会获取数据并获取直线方程,随机选择斜率和截距,直到找到最佳拟合线。 如果我们输入该算法的数据仅包含一个自变量,则称为简单线性回归。

另一方面,如果数据具有多个自变量,则回归变为多元线性回归。 线性回归的数学形式很简单,如下所示。
y= a0+a1x+ c
这里,y 是因变量,a0 和 a1 是该算法任务要找到的系数,x 是因变量,c 是这条直线的截距值。
逻辑回归
毋庸置疑,逻辑回归是监督学习算法下最直接但功能最强大的分类机器学习算法之一。 该算法可用于回归问题,但主要用于解决分类问题。 我们从该算法获得的输出始终介于 0 和 1 之间,因此使用阈值分类值将实例分类为类变得毫不费力。

名称中的逻辑一词是指激活函数,在此回归中使用。 在这种情况下,激活函数或逻辑函数实际上只是 sigmoid 函数。 这是这个 sigmoid 函数的特性,它使逻辑回归的值始终在零和一之间。 sigmoid 函数看起来像这样:
![]()
这里,y 是通过 sigmoid 函数的输出,x 是自变量。 在逻辑回归的情况下,变量 x 实际上是整个线性回归方程。 因此,可以开发逻辑回归方程,如下所示:

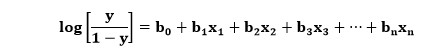
这里,变量的含义与逻辑回归中的类似,x是自变量,y是因变量,b0、b1、b2等是该算法确定的系数。
线性回归和逻辑回归之间的区别
下面列出了线性回归与逻辑回归的综合比较:
| 线性回归 | 逻辑回归 |
| 它需要标记良好的数据,这意味着它需要监督,并且用于回归。 因此,线性回归是一种有监督的回归算法。 | 它还要求输入的数据进行良好的标记。 但是,该算法用于分类而不是回归。 所以逻辑回归是一种有监督的分类算法。 |
| 通过线性回归算法得到的预测值通常可以在负无穷到正无穷的范围内。 | 通过逻辑回归获得的预测实际上在零到一的范围内。 此功能允许在阈值的帮助下轻松分类。 |
| 线性回归不需要激活函数。 | 这里我们需要一个激活函数。 在这种情况下,该函数是 sigmoid 函数。 |
| 线性回归没有阈值。 | 在逻辑回归中,需要一个阈值来正确确定每个实例的类别。 |
| 在线性回归的情况下,因变量必须是连续的。 这意味着我们不能传入变量,它是分类的并且期望在预测中具有连续值。 | 在逻辑回归的情况下,因变量必须是分类的。 这意味着它应该有不同的类别(不超过两个)。 |
| 该算法的目标是通过训练数据点找到最佳拟合线。 因此,如果拟合既不超过也不低于,我们绘制的所得直线应该几乎触及所有训练点。 | 如果我们对逻辑回归曲线的系数进行任何更改,那么它的整个图都会改变它的形状。 |
| 为了预测这些值,线性回归算法做了一个基本假设。 它假设传入该算法的值遵循标准正态分布或按照高斯分布分布。 | 逻辑回归算法还假设传递给 sigmoid 函数的数据的分布。 它假设数据服从二项分布。 |
想了解更多?
如果您有兴趣了解有关机器学习的更多信息,请查看 IIIT-B 和 upGrad 的机器学习和人工智能 PG 文凭,该文凭专为工作专业人士设计,提供 450 多个小时的严格培训、30 多个案例研究和作业、IIIT- B 校友身份、5 个以上实用的实践顶点项目和顶级公司的工作协助。
使用逻辑回归有什么缺点?
逻辑回归模型通过检查一个或多个预先存在的自变量之间的联系来预测因数据变量。 逻辑回归通常用于分类任务,有很多优点,但也有一些缺点。 在处理高维数据集时,可能会出现模型过拟合,导致结论不准确。 由于在采用逻辑回归时数据准备是一个耗时的过程,因此数据维护也变得困难。 逻辑回归的主要缺点之一是它不能处理非线性问题。
多项逻辑回归是什么意思?
多项逻辑回归是一种二元逻辑回归扩展,可以处理两个以上的因变量或结果变量。 它类似于逻辑回归,除了有许多可能的结果而不仅仅是一个。 它是一种具有多类分类能力的传统监督机器学习方法。 多项逻辑模型包括各种假设,其中之一是数据被认为是特定于案例的,这意味着每个自变量对于每个实例都有一个值。 多项逻辑模型还假定,在任何给定情况下,因变量无法从自变量中精确预测。
如何使用线性回归来解决现实生活中的问题?
线性回归广泛用于各种现实世界的情况和领域。 企业通常利用线性回归来了解广告、支出和利润之间的关系。 医学研究人员经常使用线性回归来检查药物剂量与患者血压之间的关联。 农业科学家经常使用线性回归来评估肥料和水对作物产量的影响。 因此,线性回归在解决实际问题中的用途是多种多样的。
