Regresja liniowa vs. Regresja logistyczna: różnica między regresją liniową a regresją logistyczną
Opublikowany: 2020-09-10Świat uczenia maszynowego nie byłby kompletny bez obecności dwóch najprostszych algorytmów uczenia maszynowego. Tak, zarówno regresja liniowa, jak i regresja logistyczna to najprostsze algorytmy uczenia maszynowego, jakie można zaimplementować. Przed omówieniem jakichkolwiek różnic między regresją liniową a logistyczną, musimy najpierw zrozumieć podstawy, na których leżą podstawy obu tych algorytmów.
Po pierwsze, oba te algorytmy mają charakter uczenia nadzorowanego. Oznacza to, że dane, które wprowadzisz do obu tych algorytmów, powinny być dobrze oznakowane. Kolejną ważną rzeczą, na którą należy zwrócić uwagę, są przypadki użycia. Od razu jedną rażącą różnicą między tymi dwoma algorytmami są przypadki użycia obu. Regresja liniowa jest używana zawsze, gdy chcemy wykonać regresję. Oznacza to, że używamy regresji liniowej za każdym razem, gdy chcemy przewidzieć liczby ciągłe, takie jak ceny domów w określonym obszarze.
Jednak w problemach klasyfikacyjnych wykorzystuje się regresję logistyczną. Oznacza to, że jeśli chcemy przewidzieć, czy dany dom jest drogi czy niedrogi (zamiast ceny), korzystamy z algorytmu regresji logistycznej. Tak, chociaż regresja logistyczna ma w nazwie słowo regresja, jest ona używana do klasyfikacji.
Takich ekscytujących subtelności jest więcej, które znajdziesz poniżej. Ale przed bezpośrednim porównaniem regresji liniowej z regresją logistyczną, najpierw dowiedzmy się więcej o każdym z tych algorytmów.
Spis treści
Regresja liniowa
Regresja liniowa to najłatwiejszy i najprostszy algorytm uczenia maszynowego do zrozumienia i wdrożenia. Jest to nadzorowany algorytm uczenia się, więc jeśli chcemy przewidzieć wartości ciągłe (lub wykonać regresję), musielibyśmy obsłużyć ten algorytm z dobrze oznaczonym zestawem danych. Ten algorytm uczenia maszynowego jest najprostszy ze względu na jego liniowy charakter. Aby pomyślnie przewidzieć przyszłe wartości, regresja liniowa próbuje poprowadzić linię prostą przez dane wprowadzone do algorytmu.
Tak więc za każdym razem, gdy jakakolwiek informacja jest wprowadzana do algorytmu regresji liniowej, pobiera dane i bierze równanie linii prostej, losowo wybierając nachylenie i przecinając, aż znajdzie linię najlepiej pasującą. Jeśli dane, które wprowadzamy do tego algorytmu, zawierają tylko jedną zmienną niezależną, nazywa się to prostą regresją liniową.

Z drugiej strony, jeśli dane mają wiele zmiennych niezależnych, regresja staje się wielokrotną regresją liniową. Matematyczna forma regresji liniowej jest po prostu formą linii prostej, co pokazano poniżej.
y= a0+a1x+ c
Tutaj y jest zmienną zależną, a0 i a1 jest współczynnikiem, który algorytm ma za zadanie znaleźć, x jest zmienną zależną, a c jest wartością przecięcia tej prostej.
Regresja logistyczna
Nie trzeba dodawać, że regresja logistyczna jest jednym z najprostszych, ale bardzo wydajnych algorytmów klasyfikacji maszynowego uczenia się w ramach algorytmu uczenia nadzorowanego. Algorytm ten może być używany do problemów regresji, ale jest używany głównie do rozwiązywania problemów klasyfikacyjnych. Dane wyjściowe, które otrzymujemy z tego algorytmu, zawsze mieszczą się w zakresie od 0 do 1, dzięki czemu klasyfikowanie instancji na klasy przy użyciu progowej wartości klasyfikacji staje się łatwe.

Słowo logistyczne w nazwie odnosi się do funkcji aktywacji, która jest używana w tej regresji. Funkcja aktywacji lub funkcja logistyczna, w tym przypadku, to w rzeczywistości nic innego jak funkcja sigmoidalna. Jest to właściwość tej funkcji sigmoidalnej, która utrzymuje wartość regresji logistycznej zawsze od zera do jednego. Funkcja sigmoid wygląda mniej więcej tak:
![]()
Tutaj y jest wynikiem funkcji sigmoid, a x jest zmienną niezależną. W przypadku regresji logistycznej zmienna x byłaby właściwie całym równaniem regresji liniowej. Stąd można opracować równanie regresji logistycznej, które jest napisane poniżej:
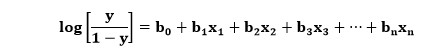
Tutaj znaczenie zmiennych jest podobne do tego w regresji logistycznej, x jest zmienną niezależną, a y jest zmienną zależną, b0, b1, b2 itd. są współczynnikami, które wyznacza ten algorytm.

Różnica między regresją liniową a logistyczną
Na poniższej liście znajdziesz kompleksowe porównanie regresji liniowej z regresją logistyczną obok siebie:
| REGRESJA LINIOWA | REGRESJA LOGISTYCZNA |
| Wymaga dobrze oznaczonych danych, co oznacza, że wymaga nadzoru i jest używany do regresji. Regresja liniowa jest zatem nadzorowanym algorytmem regresji. | Wymaga również, aby dane, które są do niego wprowadzane, były dobrze oznakowane. Jednak ten algorytm jest używany do klasyfikacji zamiast regresji. Tak więc regresja logistyczna jest nadzorowanym algorytmem klasyfikacji. |
| Predykcja uzyskana za pomocą algorytmu regresji liniowej jest zwykle wartością, która może mieścić się w zakresie od ujemnej nieskończoności do dodatniej nieskończoności. | Przewidywanie uzyskane dzięki regresji logistycznej w rzeczywistości mieści się w zakresie zaledwie od zera do jednego. Ta funkcja pozwala na łatwą klasyfikację za pomocą wartości progowej. |
| Regresja liniowa nie wymaga funkcji aktywacji. | Tutaj potrzebujemy funkcji aktywacji. W tym przypadku ta funkcja jest funkcją sigmoidalną. |
| W regresji liniowej nie ma wartości progowej. | W regresji logistycznej do prawidłowego określenia klas każdej instancji potrzebna jest wartość progowa. |
| Zmienna zależna w przypadku regresji liniowej musi mieć charakter ciągły. Oznacza to, że nie możemy przekazać zmiennej, która jest kategoryczna i oczekujemy ciągłej wartości w predykcji. | Zmienna zależna w przypadku regresji logistycznej musi być kategoryczna. Oznacza to, że powinien mieć różne kategorie (nie więcej niż dwie). |
| Celem tego algorytmu jest znalezienie linii najlepszego dopasowania przez treningowe punkty danych. Zatem wynikowa linia prosta, którą narysujemy, powinna dotykać prawie wszystkich punktów treningowych, jeśli dopasowanie nie jest ani nad, ani pod. | Jeśli dokonamy jakichkolwiek zmian we współczynniku krzywej regresji logistycznej, to cały jej wykres zmieni swój kształt. |
| Do przewidywania wartości algorytm regresji liniowej przyjmuje podstawowe założenie. Zakłada, że wartości przekazywane do tego algorytmu są zgodne ze standardowym rozkładem normalnym lub są rozłożone zgodnie z rozkładem Gaussa. | Algorytm regresji logistycznej zakłada również rozkład danych przekazywanych do funkcji sigmoidalnej. Zakłada, że dane są zgodne z rozkładem dwumianowym. |
Chcesz dowiedzieć się więcej?
Jeśli chcesz dowiedzieć się więcej o uczeniu maszynowym, sprawdź dyplom PG IIIT-B i upGrad w uczeniu maszynowym i sztucznej inteligencji, który jest przeznaczony dla pracujących profesjonalistów i oferuje ponad 450 godzin rygorystycznego szkolenia, ponad 30 studiów przypadków i zadań, IIIT- Status absolwenta B, ponad 5 praktycznych, praktycznych projektów zwieńczenia i pomoc w pracy z najlepszymi firmami.
Jakie są wady korzystania z regresji logistycznej?
Model regresji logistycznej przewiduje zależną zmienną danych, badając związek między jedną lub kilkoma wcześniej istniejącymi zmiennymi niezależnymi. Regresja logistyczna, która jest powszechnie stosowana do zadań klasyfikacyjnych, ma wiele zalet, ale ma też pewne wady. Podczas pracy z wielowymiarowymi zestawami danych może wystąpić nadmierne dopasowanie modelu, co skutkuje niedokładnymi wnioskami. Ponieważ przygotowanie danych jest procedurą czasochłonną w przypadku regresji logistycznej, utrzymanie danych również staje się trudne. Jedną z głównych wad regresji logistycznej jest to, że nie radzi sobie z problemami nieliniowymi.
Co oznacza wielomianowa regresja logistyczna?
Wielomianowa regresja logistyczna to binarne rozszerzenie regresji logistycznej, które może obsługiwać więcej niż dwie zmienne zależne lub wynikowe. Jest podobny do regresji logistycznej, z tą różnicą, że istnieje wiele możliwych wyników, a nie tylko jeden. Jest to tradycyjne podejście do nadzorowanego uczenia maszynowego z możliwościami klasyfikacji wieloklasowej. Wielomianowy model logistyczny zawiera różne założenia, z których jedno jest takie, że dane są uważane za specyficzne dla przypadku, co oznacza, że każda zmienna niezależna ma jedną wartość dla każdej instancji. Wielomianowy model logistyczny zakłada również, że w dowolnym scenariuszu zmienna zależna nie może być precyzyjnie przewidziana na podstawie zmiennych niezależnych.
Jak można wykorzystać regresję liniową do rozwiązywania rzeczywistych problemów?
Regresja liniowa jest szeroko stosowana w różnych rzeczywistych sytuacjach i sektorach. Firmy zazwyczaj wykorzystują regresję liniową, aby zrozumieć związek między reklamą, wydatkami i zyskiem. Badacze medyczni często stosują regresję liniową w celu zbadania związku między dawką leku a ciśnieniem krwi pacjenta. Naukowcy zajmujący się rolnictwem często stosują regresję liniową do oceny wpływu nawozów i wody na plony. W związku z tym zastosowania regresji liniowej są zróżnicowane w rozwiązywaniu rzeczywistych problemów.
