Régression linéaire Vs. Régression logistique : différence entre la régression linéaire et la régression logistique
Publié: 2020-09-10Le monde de l'apprentissage automatique ne serait pas complet sans la présence de deux des algorithmes d'apprentissage automatique les plus simples. Oui, la régression linéaire et la régression logistique sont les algorithmes d'apprentissage automatique les plus simples que vous puissiez mettre en œuvre. Avant de discuter de l'une des différences entre la régression linéaire et la régression logistique, nous devons d'abord comprendre les bases sur lesquelles reposent les fondements de ces deux algorithmes.
Tout d'abord, ces deux algorithmes sont par nature un apprentissage supervisé. Cela signifie que les données que vous alimenterez dans ces deux algorithmes doivent être bien étiquetées. Une autre chose essentielle à noter est les cas d'utilisation. Dès le départ, une différence flagrante entre ces deux algorithmes réside dans les cas d'utilisation des deux. La régression linéaire est utilisée chaque fois que nous souhaitons effectuer une régression. Cela signifie que nous utilisons la régression linéaire chaque fois que nous voulons prédire des nombres continus, comme les prix des maisons dans une zone particulière.
Cependant, l'utilisation de la régression logistique se fait dans les problèmes de classification. Autrement dit, si nous voulons prédire si une maison particulière est chère ou bon marché (au lieu du prix), nous utilisons l'algorithme de régression logistique. Oui, même si la régression logistique a le mot régression dans son nom, elle est utilisée pour la classification.
Il existe d'autres subtilités passionnantes que vous trouverez ci-dessous. Mais avant de comparer directement la régression linéaire à la régression logistique, apprenons d'abord plus sur chacun de ces algorithmes.
Table des matières
Régression linéaire
La régression linéaire est l'algorithme d'apprentissage automatique le plus facile et le plus simple à comprendre et à déployer. C'est un algorithme d'apprentissage supervisé, donc si nous voulons prédire les valeurs continues (ou effectuer une régression), nous devons servir cet algorithme avec un ensemble de données bien étiqueté. Cet algorithme d'apprentissage automatique est le plus simple en raison de sa nature linéaire. Pour prédire avec succès les valeurs futures, la régression linéaire essaie de tracer une ligne droite à travers les données introduites dans l'algorithme.
Ainsi, chaque fois qu'une information est introduite dans un algorithme de régression linéaire, il prend les données et prend l'équation d'une ligne droite, sélectionnant au hasard la pente et l'interception jusqu'à ce qu'il trouve la ligne de meilleur ajustement. Si les données que nous alimentons dans cet algorithme ne contiennent qu'une seule variable indépendante, cela s'appelle une régression linéaire simple.

D'autre part, si les données ont plusieurs variables indépendantes, la régression devient une régression linéaire multiple. La forme mathématique de la régression linéaire est simplement celle d'une ligne droite, qui est illustrée ci-dessous.
y= a0+a1x+ c
Ici, y est la variable dépendante, a0 et a1 est le coefficient que cet algorithme est chargé de trouver, x est la variable dépendante et c est la valeur d'interception de cette ligne droite.
Régression logistique
Il va sans dire que la régression logistique est l'un des algorithmes d'apprentissage automatique de classification les plus simples mais les plus puissants sous l'égide d'un algorithme d'apprentissage supervisé. Cet algorithme peut être utilisé pour des problèmes de régression, mais il est plutôt utilisé pour résoudre des problèmes de classification. La sortie que nous obtenons de cet algorithme est toujours comprise entre 0 et 1, grâce à quoi il devient facile de classer les instances en classes en utilisant une valeur de classification seuil.

Le mot logistique dans le nom fait référence à la fonction d'activation, qui est utilisée dans cette régression. La fonction d'activation ou la fonction logistique, dans ce cas, n'est en fait rien d'autre que la fonction sigmoïde. C'est la propriété de cette fonction sigmoïde, qui maintient toujours la valeur de la régression logistique entre zéro et un. La fonction sigmoïde ressemble à ceci :
![]()
Ici, y est la sortie via la fonction sigmoïde et x est la variable indépendante. Dans le cas de la régression logistique, la variable x serait en fait l'équation de régression linéaire entière. Par conséquent, l'équation de régression logistique peut être développée, qui est écrite ci-dessous :
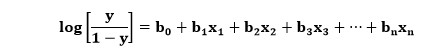
Ici, la signification des variables est similaire à celle de la régression logistique, x est la variable indépendante, et y est la variable dépendante, b0, b1, b2, etc., sont le coefficient que cet algorithme détermine.

Différence entre régression linéaire et régression logistique
Ci-dessous, vous trouverez une comparaison complète de la régression linéaire par rapport à la régression logistique côte à côte :
| RÉGRESSION LINÉAIRE | RÉGRESSION LOGISTIQUE |
| Il nécessite des données bien étiquetées, ce qui signifie qu'il nécessite une supervision, et il est utilisé pour la régression. Ainsi, la régression linéaire est un algorithme de régression supervisée. | Cela nécessite également que les données qui y sont introduites soient bien étiquetées. Cependant, cet algorithme est utilisé pour la classification au lieu de la régression. La régression logistique est donc un algorithme de classification supervisée. |
| La prédiction obtenue grâce à l'algorithme de régression linéaire est généralement une valeur qui peut être comprise entre l'infini négatif et l'infini positif. | La prédiction obtenue grâce à la régression logistique est en fait de l'ordre de zéro à un. Cette fonctionnalité permet une classification facile à l'aide d'une valeur seuil. |
| La régression linéaire ne nécessite aucune fonction d'activation. | Ici nous avons besoin d'une fonction d'activation. Dans ce cas, cette fonction est la fonction sigmoïde. |
| Il n'y a pas de valeur seuil dans la régression linéaire. | Dans la régression logistique, une valeur seuil est nécessaire pour déterminer correctement les classes de chaque instance. |
| La variable dépendante dans le cas de la régression linéaire doit être de nature continue. Cela signifie que nous ne pouvons pas transmettre la variable, qui est catégorique et s'attendre à une valeur continue dans la prédiction. | La variable dépendante dans le cas de la régression logistique doit être catégorique. Cela signifie qu'il devrait avoir différentes catégories (pas plus de deux). |
| Le but de cet algorithme est de trouver la ligne de meilleur ajustement à travers les points de données d'apprentissage. Ainsi, la ligne droite résultante, que nous traçons, devrait toucher presque tous les points d'entraînement si l'ajustement n'est ni supérieur ni inférieur. | Si nous apportons des modifications au coefficient de la courbe de régression logistique, l'ensemble de son tracé changerait de forme. |
| Pour prédire les valeurs, l'algorithme de régression linéaire fait une hypothèse fondamentale. Il suppose que les valeurs qui sont passées dans cet algorithme suivent la distribution normale standard ou sont distribuées conformément à la distribution gaussienne. | L'algorithme de régression logistique fait également une hypothèse sur la distribution des données transmises à la fonction sigmoïde. Il suppose que les données suivent la distribution binomiale. |
Vous voulez en savoir plus ?
Si vous souhaitez en savoir plus sur l'apprentissage automatique, consultez le diplôme PG en apprentissage automatique et IA de IIIT-B & upGrad, conçu pour les professionnels en activité et offrant plus de 450 heures de formation rigoureuse, plus de 30 études de cas et missions, IIIT- Statut B Alumni, plus de 5 projets de synthèse pratiques et aide à l'emploi avec les meilleures entreprises.
Quels sont les inconvénients de l'utilisation de la régression logistique ?
Un modèle de régression logistique anticipe une variable de données dépendante en examinant la connexion entre une ou plusieurs variables indépendantes préexistantes. La régression logistique, couramment utilisée pour les tâches de classification, présente de nombreux avantages, mais elle présente également certains inconvénients. Lorsque vous travaillez avec des ensembles de données de grande dimension, un surajustement du modèle peut se produire, entraînant des conclusions inexactes. Étant donné que la préparation des données est une procédure qui prend du temps lors de l'utilisation de la régression logistique, la maintenance des données devient également difficile. L'un des inconvénients majeurs de la régression logistique est qu'elle ne peut pas traiter les problèmes non linéaires.
Qu'entend-on par régression logistique multinomiale ?
La régression logistique multinomiale est une extension de régression logistique binaire qui peut gérer plus de deux variables dépendantes ou de résultat. Il est similaire à la régression logistique, sauf qu'il existe de nombreux résultats possibles plutôt qu'un seul. Il s'agit d'une approche traditionnelle d'apprentissage automatique supervisé avec des capacités de classification multi-classes. Le modèle logistique multinomial comprend diverses hypothèses, dont l'une est que les données sont considérées comme spécifiques au cas, ce qui signifie que chaque variable indépendante a une valeur unique pour chaque instance. Le modèle logistique multinomial postule également que dans un scénario donné, la variable dépendante ne peut pas être prédite avec précision à partir des variables indépendantes.
Comment la régression linéaire peut-elle être utilisée pour résoudre des problèmes réels ?
La régression linéaire est largement utilisée dans une variété de situations et de secteurs du monde réel. Les entreprises utilisent généralement la régression linéaire pour comprendre la relation entre la publicité, les dépenses et les bénéfices. Les chercheurs médicaux utilisent fréquemment la régression linéaire pour examiner l'association entre la dose de médicament et la tension artérielle du patient. Les agronomes utilisent fréquemment la régression linéaire pour évaluer l'influence des engrais et de l'eau sur les rendements des cultures. Ainsi, les utilisations de la régression linéaire sont variées dans la résolution de problèmes réels.
