數據結構中的圖：類型、存儲和遍歷

數據結構是在數據科學中組織數據的一種有效方式，以便可以輕鬆訪問和有效使用數據。 有許多類型的數據庫，但本文討論了為什麼圖在數據管理中起著至關重要的作用。

劇透警報：您每天都使用數據結構中的圖表來獲取前往辦公室的最佳路線，獲取有關您的午餐、電影的建議並優化您的下一個飛行路線。 聽起來不錯！ 讓我們看看圖表的屬性及其應用。

首先，讓我們看看Graph 是什麼？ 它是由節點（或頂點）和邊（或路徑）組成的非線性結構中的數據表示。

數據結構中的圖可以稱為由存儲在許多相互連接的邊（路徑）和頂點（節點）組之間的數據組成的數據結構。 圖數據結構（N，E）由節點和邊的集合構成。 節點和頂點都需要是有限的。

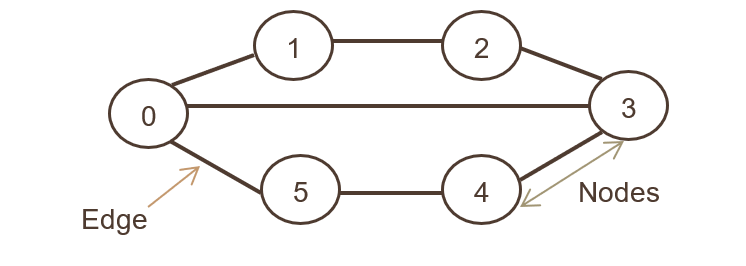
在上面的圖形表示中，節點集是 N={0,1,2,3,4,5,6}，邊集是

G={01,12,23,34,45,05,03}

現在讓我們研究一下圖表的類型。

閱讀：十大數據可視化技術

圖表類型

1.加權圖

邊或路徑有值的圖。 所有與邊緣相關的值都稱為權重。 邊值可以代表重量/成本/長度。

值或權重也可以表示：

• 兩點之間的距離- 例如：尋找到辦公室的最短路徑，辦公室網絡中兩個工作站之間的距離。
• 數據包在網絡或帶寬中的速度。

2. 未加權圖

沒有與邊緣相關的價值或權重。 默認情況下，除非有關聯的值，否則所有圖表均未加權。

3. 無向圖

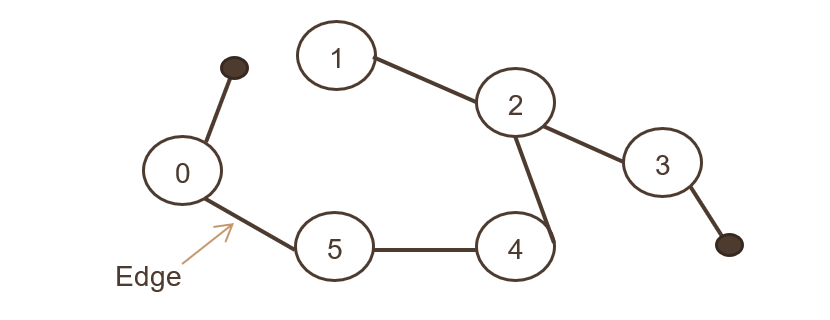
連接一組對象，並且所有邊都是雙向的。 下圖展示了無向圖，

這就像兩個 Facebook 用戶在連接為朋友後的關聯性。 兩個用戶都可以互相參考和分享照片、評論。

4.有向圖

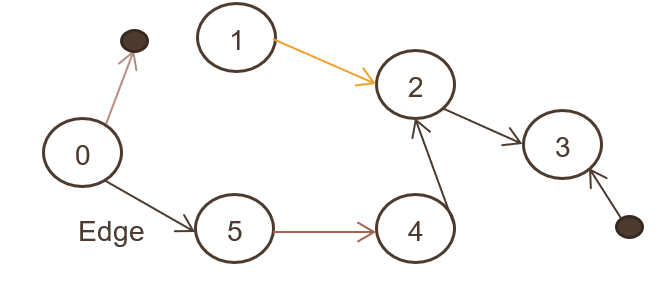
也稱為有向圖，其中連接了一組對象（N，E），並且所有邊都從一個節點指向另一個節點。 上圖展示了有向圖。

結帳：您可以復制的數據可視化項目

圖的存儲

每種存儲方式都有其優缺點，根據複雜程度選擇合適的存儲方式。 存儲圖形最常用的兩種數據結構是：

1.鄰接表

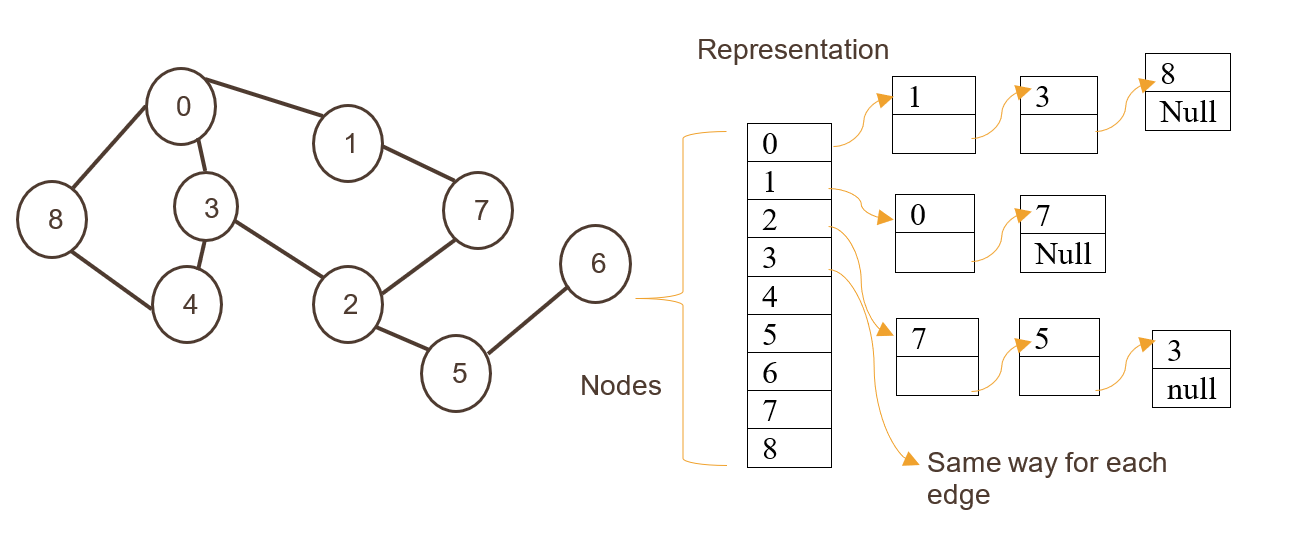
這裡節點存儲為一維數組的索引，然後邊存儲為列表。

2.鄰接矩陣

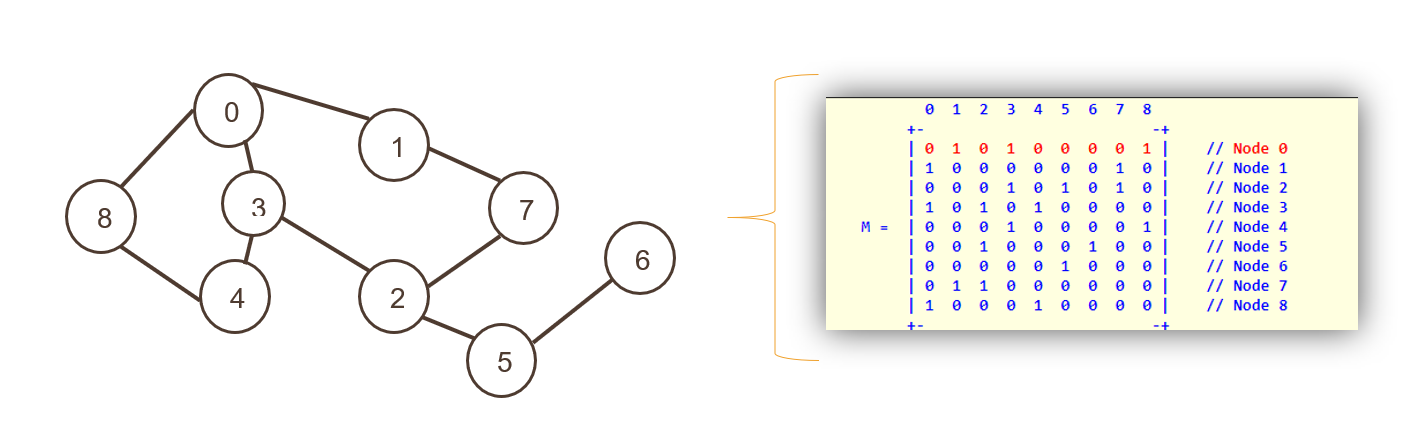
這裡節點表示為二維數組的索引，然後是表示為相鄰矩陣的非零值的邊。

行和列都展示了節點； 整個矩陣用“0”或“1”填充，代表真或假。 零表示沒有路徑，1 表示有路徑。

圖遍歷

圖遍歷是一種用於在圖中搜索節點的方法。 圖遍歷用於決定用於節點排列的順序。 它還可以在不創建循環的情況下搜索邊，這意味著可以在不創建循環的情況下搜索所有節點和邊。

有兩種圖遍歷結構。

1. DFS（Depth First Search）：深度搜索方法

DFS 搜索從第一個節點開始，越來越深，向下探索，直到找到目標節點。 如果未找到目標鍵，則將搜索路徑更改為在初始搜索期間停止探索的路徑，並對該分支重複相同的過程。

生成樹是根據該搜索的結果生成的。 這種樹方法沒有循環。 堆棧數據結構中的節點總數用於實現DFS遍歷。

實現 DFS 搜索的步驟：

第 1 步 – 需要根據節點總數定義堆棧大小。

步驟 2 – 選擇初始節點進行橫向； 需要通過訪問該節點將其推送到堆棧。

第 3 步 – 現在，訪問之前未訪問過的相鄰節點並將其推送到堆棧中。

第 4 步——重複第 3 步，直到沒有未訪問的相鄰節點。

步驟 5 – 當沒有其他節點可以訪問時，使用回溯和一個節點。

步驟 6 – 通過重複步驟 3、4 和 5 清空堆棧。

第 7 步 – 當堆棧為空時，通過消除未使用的邊形成最終生成樹。

DFS 的應用有：

• 僅用一種解決方案即可解決難題。
• 測試一個圖是否是二分圖。
• 用於調度作業和許多其他的拓撲排序。

2、BFS（Breadth-First Search）：使用排隊的方式實現搜索

廣度優先搜索以廣度運動導航圖，並在遇到路徑結束後利用基於隊列從一個節點跳轉到另一個節點。

實施 BFS 搜索的步驟，

第 1 步 – 根據節點的數量，定義隊列。

第 2 步 – 從遍歷的任何節點開始。 訪問該節點並將其添加到隊列中。

第 3 步 - 現在檢查隊列前面的未訪問的相鄰節點，並將其添加到隊列中，而不是添加到開頭。

第 4 步 – 現在開始刪除沒有任何需要訪問的邊且不在隊列中的節點。

第 5 步 – 通過重複第 4 步和第 5 步清空隊列。

第 6 步 – 僅在隊列為空後移除未使用的邊並形成生成樹。

BFS 的應用有：

• 點對點網絡——就像在 Bittorrent 中一樣，它用於查找所有相鄰節點。
• 搜索引擎中的爬蟲。
• 社交網絡網站等等。

圖在數據結構中的實際應用

圖表用於許多日常應用，如網絡表示（道路、光纖映射、設計電路板等）。 例如：在 Facebook 數據網絡中，節點代表用戶、他/她的照片或評論，邊代表照片、對照片的評論。

數據結構中的圖具有廣泛的應用。 其中一些值得注意的是：

• 社交圖譜 API——這是數據在 Facebook 社交媒體平台內外交流的主要方式。 它是一個基於 HTTP 的 API，用於以編程方式查詢數據、上傳照片和視頻、製作新故事以及許多其他任務。 它由節點、邊和字段組成； 要查詢，使用特定的對象節點。 受單個對象和字段影響的一組對象的邊緣用於獲取有關組中每個對象的數據。
• Yelp 的 GraphQL API – 這是一個推薦引擎，用於從 Yelp 平台獲取特定數據。 在這裡，訂單用於查找邊，然後查詢特定節點以獲取確切結果。 這加快了檢索過程。

在 Yelp 平台上，節點代表業務，包含 id、name、is_close 和許多其他圖形屬性。

• 路徑優化算法——它們用於找到符合速度、安全、燃料等標準的最佳連接。該算法中使用了 BFS。 最好的例子是谷歌地圖平台（地圖、路線 API）。
• Flight Networks - 在飛行網絡中，這用於找到適合圖形數據結構的優化路徑。 這也有助於模型並有效地優化機場程序。

另請閱讀：數據可視化的好處

結論

在本文中，我們首先討論了圖和圖在數據結構中的定義，然後了解了圖的類型及其屬性。 後來，我們了解了常用的圖存儲方法，然後是 Graphs 中使用的重要主題搜索方法，Graph Traversal。 最後，我們討論了圖數據結構的實際應用。

本文提供了有關數據結構中圖的見解； 了解這一點對於圖數據庫、搜索算法實現、編程等方面的基本理解至關重要。 必須向行業專家學習。

為什麼選擇 upGrad 課程？

我們建議您選擇在 upGrad 上託管的 IIIT Bangalore 提供的數據科學執行 PG 計劃，因為在這裡您可以與課程講師進行 1-1 的查詢。 它不僅注重理論學習，而且重視基於實踐的知識，這對於讓學習者為面對現實世界的項目做好準備並為您提供印度第一個 NASSCOM 證書，這有助於您獲得數據科學領域的高薪工作。

參考文獻

數學/計算機系 - 主頁，www.mathcs.emory.edu/~cheung/Courses/171/Syllabus/11-Graph/data-stru.html。

“數學洞察力。” 有向圖定義 - Math Insight ，mathinsight.org/definition/directed_graph。

辛格，阿姆裡帕爾。 “圖形數據結構。” 中，中，2020 年 3 月 29 日，medium.com/@singhamritpal49/graph-data-structure-49427c81b3b3。

獨奏。 “你必須知道的圖形數據結構的實際應用。” Graph Data and GraphQL API Development-Leap Graph ，leapgraph.com/graph-data-structures-applications。