数据结构中的图：类型、存储和遍历

数据结构是在数据科学中组织数据的一种有效方式，以便可以轻松访问和有效使用数据。 有许多类型的数据库，但本文讨论了为什么图在数据管理中起着至关重要的作用。

剧透警报：您每天都使用数据结构中的图表来获取前往办公室的最佳路线，获取有关您的午餐、电影的建议并优化您的下一个飞行路线。 听起来不错！ 让我们看看图表的属性及其应用。

首先，让我们看看Graph 是什么？ 它是由节点（或顶点）和边（或路径）组成的非线性结构中的数据表示。

数据结构中的图可以称为由存储在许多相互连接的边（路径）和顶点（节点）组之间的数据组成的数据结构。 图数据结构（N，E）由节点和边的集合构成。 节点和顶点都需要是有限的。

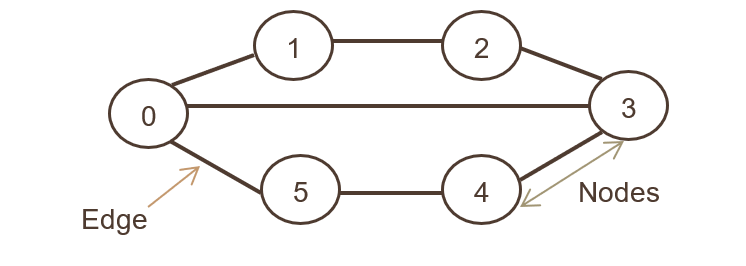
在上面的图形表示中，节点集是 N={0,1,2,3,4,5,6}，边集是

G={01,12,23,34,45,05,03}

现在让我们研究一下图表的类型。

阅读：十大数据可视化技术

图表类型

1.加权图

边或路径有值的图。 所有与边缘相关的值都称为权重。 边值可以代表重量/成本/长度。

值或权重也可以表示：

• 两点之间的距离- 例如：寻找到办公室的最短路径，办公室网络中两个工作站之间的距离。
• 数据包在网络或带宽中的速度。

2. 未加权图

没有与边缘相关的价值或权重。 默认情况下，除非有关联的值，否则所有图表均未加权。

3. 无向图

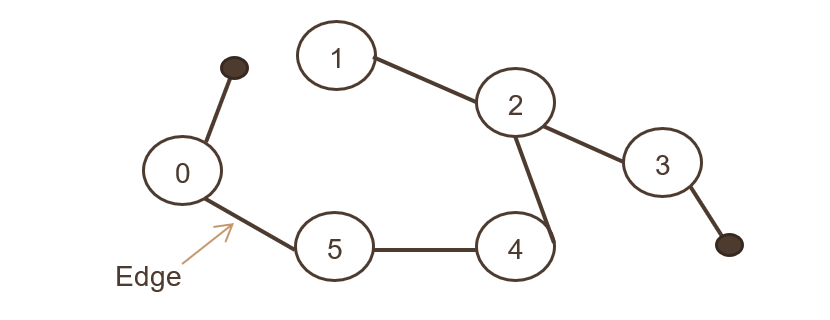
连接一组对象，并且所有边都是双向的。 下图展示了无向图，

这就像两个 Facebook 用户在连接为朋友后的关联性。 两个用户都可以互相参考和分享照片、评论。

4.有向图

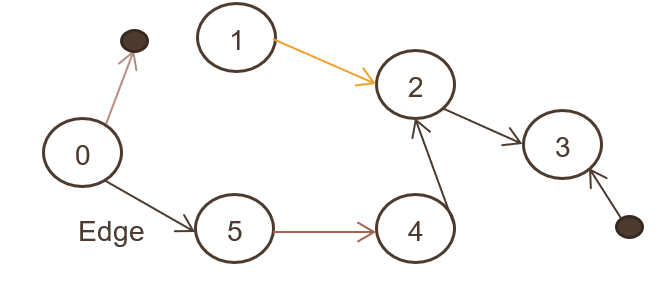
也称为有向图，其中连接了一组对象（N，E），并且所有边都从一个节点指向另一个节点。 上图展示了有向图。

结帐：您可以复制的数据可视化项目

图的存储

每种存储方式都有其优缺点，根据复杂程度选择合适的存储方式。 存储图形最常用的两种数据结构是：

1.邻接表

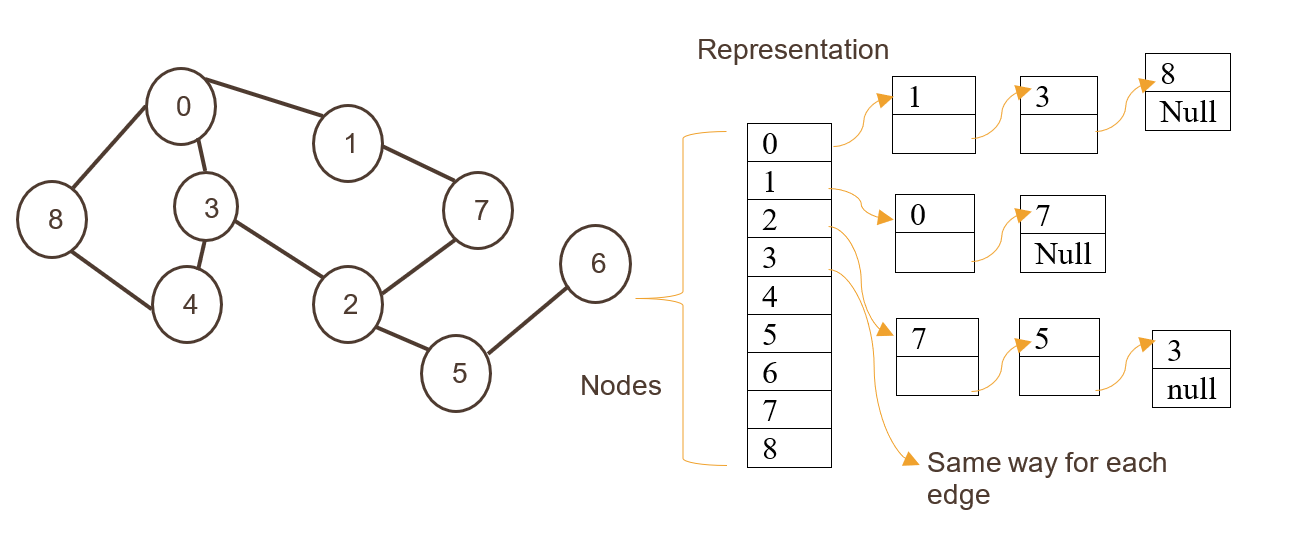
这里节点存储为一维数组的索引，然后边存储为列表。

2.邻接矩阵

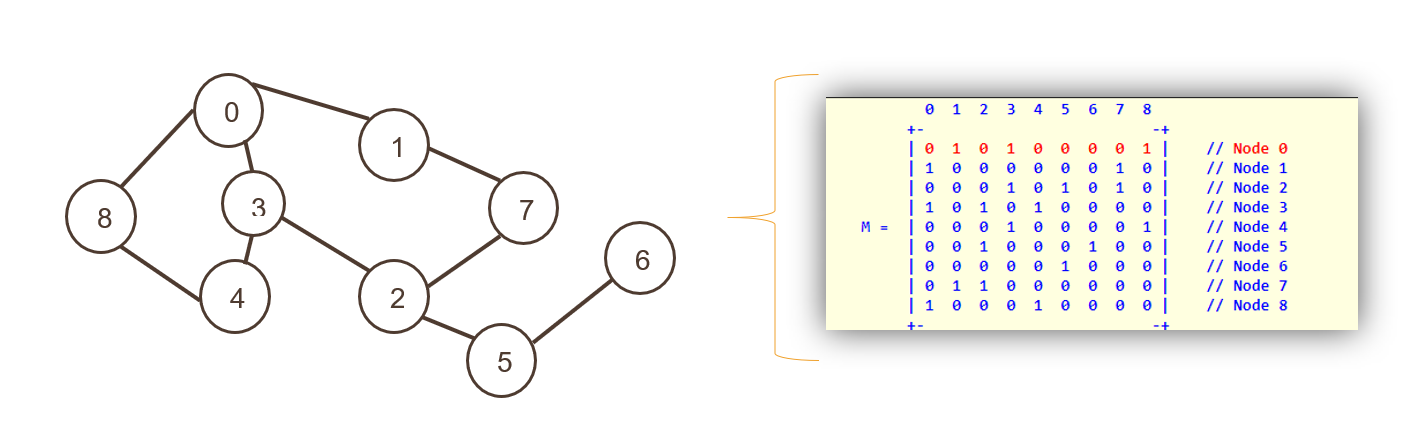
这里节点表示为二维数组的索引，然后是表示为相邻矩阵的非零值的边。

行和列都展示了节点； 整个矩阵用“0”或“1”填充，代表真或假。 零表示没有路径，1 表示有路径。

图遍历

图遍历是一种用于在图中搜索节点的方法。 图遍历用于决定用于节点排列的顺序。 它还可以在不创建循环的情况下搜索边，这意味着可以在不创建循环的情况下搜索所有节点和边。

有两种图遍历结构。

1. DFS（Depth First Search）：深度搜索方法

DFS 搜索从第一个节点开始，越来越深，向下探索，直到找到目标节点。 如果未找到目标键，则将搜索路径更改为在初始搜索期间停止探索的路径，并对该分支重复相同的过程。

生成树是根据该搜索的结果生成的。 这种树方法没有循环。 堆栈数据结构中的节点总数用于实现DFS遍历。

实现 DFS 搜索的步骤：

第 1 步 – 需要根据节点总数定义堆栈大小。

步骤 2 – 选择初始节点进行横向； 需要通过访问该节点将其推送到堆栈。

第 3 步 – 现在，访问之前未访问过的相邻节点并将其推送到堆栈中。

第 4 步——重复第 3 步，直到没有未访问的相邻节点。

步骤 5 – 当没有其他节点可以访问时，使用回溯和一个节点。

步骤 6 – 通过重复步骤 3、4 和 5 清空堆栈。

第 7 步 – 当堆栈为空时，通过消除未使用的边形成最终生成树。

DFS 的应用有：

• 仅用一种解决方案即可解决难题。
• 测试一个图是否是二分图。
• 用于调度作业和许多其他的拓扑排序。

2、BFS（Breadth-First Search）：使用排队的方式实现搜索

广度优先搜索以广度运动导航图，并在遇到路径结束后利用基于队列从一个节点跳转到另一个节点。

实施 BFS 搜索的步骤，

第 1 步 – 根据节点的数量，定义队列。

第 2 步 – 从遍历的任何节点开始。 访问该节点并将其添加到队列中。

第 3 步 - 现在检查队列前面的未访问的相邻节点，并将其添加到队列中，而不是添加到开头。

第 4 步 – 现在开始删除没有任何需要访问的边且不在队列中的节点。

第 5 步 – 通过重复第 4 步和第 5 步清空队列。

第 6 步 – 仅在队列为空后移除未使用的边并形成生成树。

BFS 的应用有：

• 点对点网络——就像在 Bittorrent 中一样，它用于查找所有相邻节点。
• 搜索引擎中的爬虫。
• 社交网络网站等等。

图在数据结构中的实际应用

图表用于许多日常应用，如网络表示（道路、光纤映射、设计电路板等）。 例如：在 Facebook 数据网络中，节点代表用户、他/她的照片或评论，边代表照片、对照片的评论。

数据结构中的图具有广泛的应用。 其中一些值得注意的是：

• 社交图谱 API——这是数据在 Facebook 社交媒体平台内外交流的主要方式。 它是一个基于 HTTP 的 API，用于以编程方式查询数据、上传照片和视频、制作新故事以及许多其他任务。 它由节点、边和字段组成； 要查询，使用特定的对象节点。 受单个对象和字段影响的一组对象的边缘用于获取有关组中每个对象的数据。
• Yelp 的 GraphQL API – 这是一个推荐引擎，用于从 Yelp 平台获取特定数据。 在这里，订单用于查找边，然后查询特定节点以获取确切结果。 这加快了检索过程。

在 Yelp 平台上，节点代表业务，包含 id、name、is_close 和许多其他图形属性。

• 路径优化算法——它们用于找到符合速度、安全、燃料等标准的最佳连接。该算法中使用了 BFS。 最好的例子是谷歌地图平台（地图、路线 API）。
• Flight Networks - 在飞行网络中，这用于找到适合图形数据结构的优化路径。 这也有助于模型并有效地优化机场程序。

另请阅读：数据可视化的好处

结论

在本文中，我们首先讨论了图和图在数据结构中的定义，然后了解了图的类型及其属性。 后来，我们了解了常用的图存储方法，然后是 Graphs 中使用的重要主题搜索方法，Graph Traversal。 最后，我们讨论了图数据结构的实际应用。

本文提供了有关数据结构中图的见解； 了解这一点对于图数据库、搜索算法实现、编程等方面的基本理解至关重要。 必须向行业专家学习。

为什么选择 upGrad 课程？

我们建议您选择在 upGrad 上托管的 IIIT Bangalore 提供的数据科学执行 PG 计划，因为在这里您可以与课程讲师进行 1-1 的查询。 它不仅注重理论学习，而且重视基于实践的知识，这对于让学习者为面对现实世界的项目做好准备并为您提供印度第一个 NASSCOM 证书，这有助于您获得数据科学领域的高薪工作。

参考文献

数学/计算机系 - 主页，www.mathcs.emory.edu/~cheung/Courses/171/Syllabus/11-Graph/data-stru.html。

“数学洞察力。” 有向图定义 - Math Insight ，mathinsight.org/definition/directed_graph。

辛格，阿姆里帕尔。 “图形数据结构。” 中，中，2020 年 3 月 29 日，medium.com/@singhamritpal49/graph-data-structure-49427c81b3b3。

独奏。 “你必须知道的图形数据结构的实际应用。” Graph Data and GraphQL API Development-Leap Graph ，leapgraph.com/graph-data-structures-applications。