Veri Yapısındaki Grafikler: Türler, Depolama ve Geçiş

Veri yapısı, veri biliminde verilere kolayca erişilebilmesi ve etkin bir şekilde kullanılabilmesi için verileri düzenlemenin etkili bir yoludur. Birçok veritabanı türü vardır, ancak bu makalede grafiklerin veri yönetiminde neden hayati bir rol oynadığı tartışılmaktadır.

Spoiler uyarısı: Ofisinize en iyi rotayı getirmek, öğle yemeğiniz, filminiz için öneriler almak ve bir sonraki uçuş rotanızı optimize etmek için her gün veri yapısında Grafikleri kullanırsınız. Kulağa ilginç geliyor! Grafiğin özelliklerini ve uygulamasını görelim.

İlk olarak, Grafiğin ne olduğunu görelim ? Düğümler (veya köşeler) ve kenarlardan (veya yollardan) oluşan doğrusal olmayan bir yapıdaki verilerin bir temsilidir.

Veri yapısındaki bir Grafik, birbirine bağlı birçok kenar (yol) ve tepe noktası (düğüm) arasında depolanan verilerden oluşan bir veri yapısı olarak adlandırılabilir. Grafik veri yapısı (N, E), Düğümler ve Kenarlar koleksiyonuyla yapılandırılmıştır. Hem düğümlerin hem de köşelerin sonlu olması gerekir.

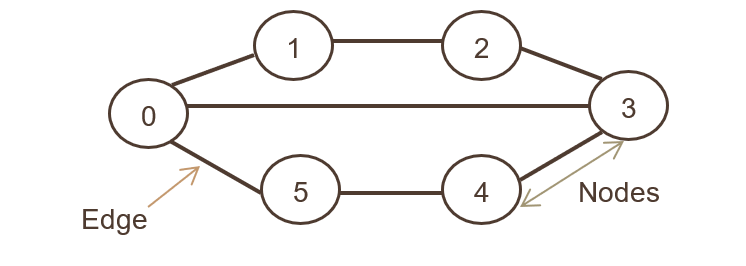
Yukarıdaki grafik gösteriminde, Düğümler Kümesi N={0,1,2,3,4,5,6}ve kenarlar kümesi

G={01,12,23,34,45,05,03}

Şimdi grafik türlerini inceleyelim.

Okuyun: En İyi 10 Veri Görselleştirme Tekniği

Grafik Türleri

1. Ağırlıklı Grafik

Kenarları veya yolları değerleri olan grafikler. Kenarlarla ilişkili görülen tüm değerlere ağırlık denir. Kenar değeri, ağırlık/maliyet/uzunluğu temsil edebilir.

Değerler veya ağırlıklar ayrıca şunları da temsil edebilir:

• İki nokta arasında kapsanan mesafe- Ör: Ofise giden en kısa yolu aramak için, bir ofis ağındaki iki iş istasyonu arasındaki mesafe.
• Bir ağdaki veya bant genişliğindeki veri paketinin hızı.

2. Ağırlıksız Grafik

Kenarla ilişkili herhangi bir değer veya ağırlık olmadığında. Varsayılan olarak, ilişkili bir değer olmadığı sürece tüm grafikler ağırlıksızdır.

3. Yönsüz Grafik

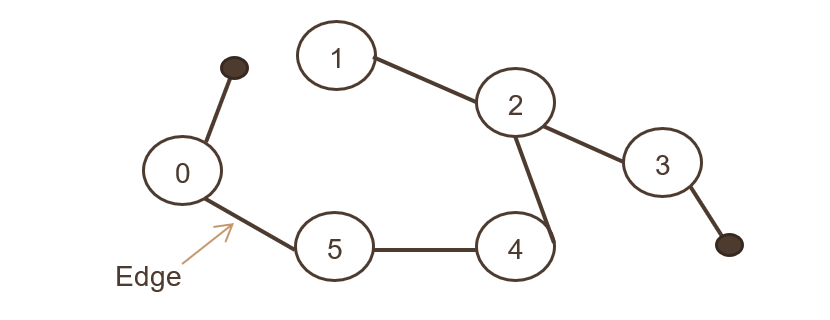
Bir dizi nesnenin bağlı olduğu ve tüm kenarların çift yönlü olduğu yer. Aşağıdaki görüntü yönsüz grafiği göstermektedir,

İki Facebook kullanıcısının arkadaş olarak bağlandıktan sonra birleşmesi gibi. Her iki kullanıcı da fotoğraflara başvurabilir ve paylaşabilir, birbirleri arasında yorum yapabilir.

4. Yönlendirilmiş Grafik

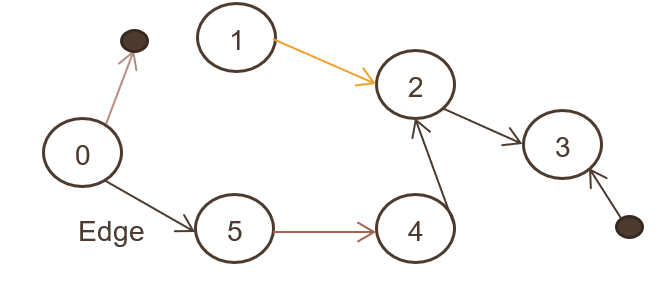
Bir dizi nesnenin (N, E) bağlı olduğu ve tüm kenarların bir düğümden diğerine yönlendirildiği bir digraf olarak da adlandırılır. Yukarıdaki görüntü yönlendirilmiş grafiği göstermektedir.

Ödeme: Çoğaltabileceğiniz Veri Görselleştirme Projeleri

Grafiğin Saklanması

Her depolama yönteminin artıları ve eksileri vardır ve karmaşıklığa göre doğru depolama yöntemi seçilir. Grafikleri depolamak için en sık kullanılan iki veri yapısı şunlardır:

1. Komşuluk listesi

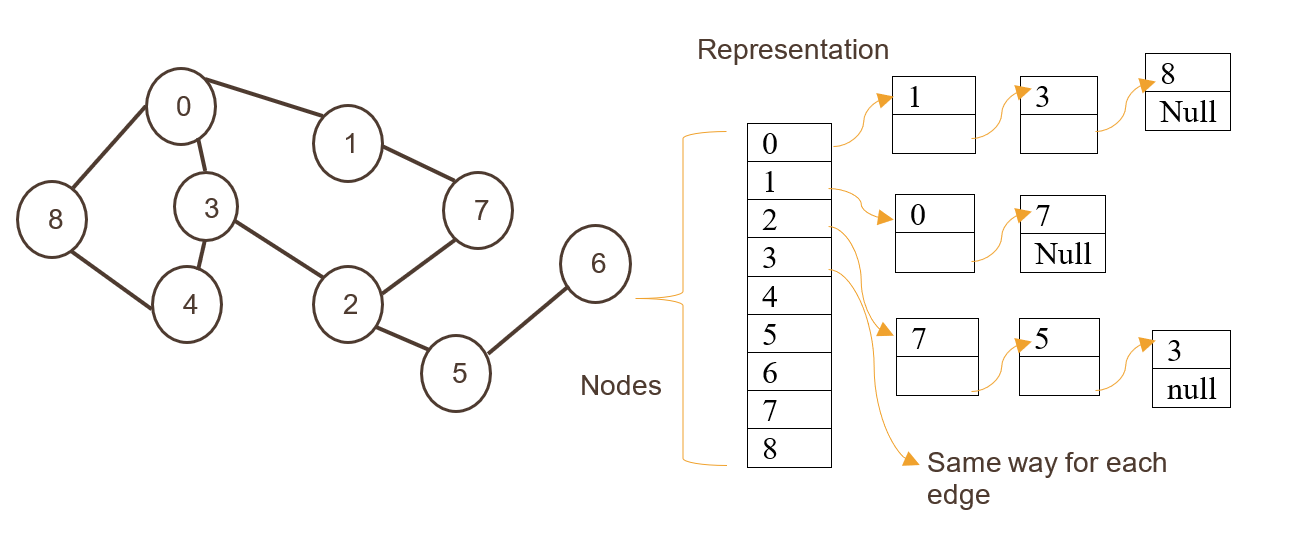
Burada düğümler, tek boyutlu dizinin bir dizini olarak depolanır, ardından kenarlar bir liste olarak depolanır.

2. Komşuluk matrisi

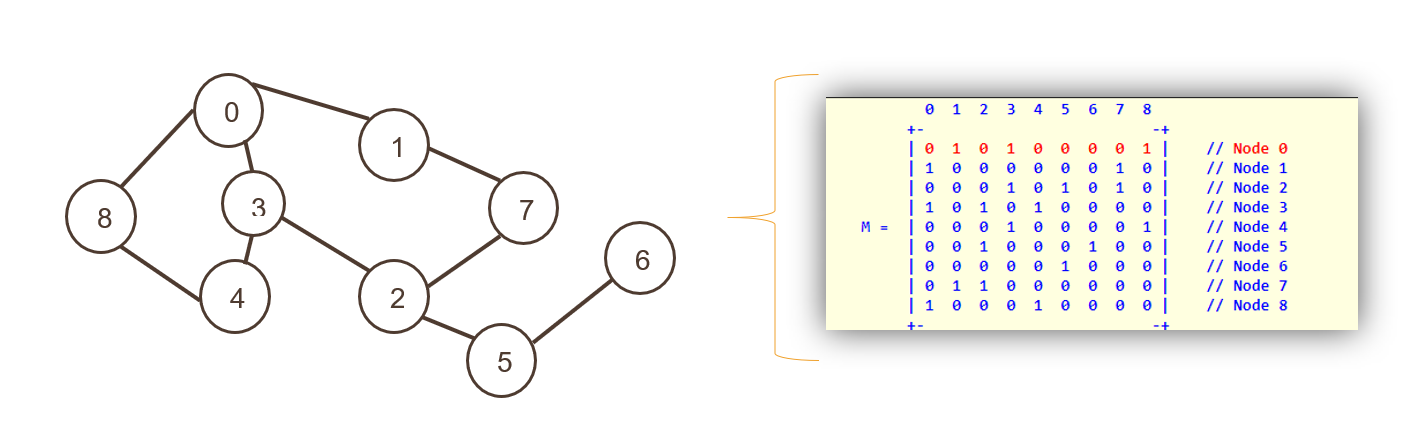
Burada düğümler, iki boyutlu bir dizinin indeksi olarak temsil edilir, ardından bitişik bir matrisin sıfır olmayan değerleri olarak temsil edilen kenarlar gelir.

Hem satırlar hem de sütunlar Düğümleri gösterir; tüm matris, doğru veya yanlışı temsil eden "0" veya "1" ile doldurulur. Sıfır, yol olmadığını ve 1 bir yolu temsil eder.

Grafik Geçişi

Grafik geçişi, bir grafikteki düğümleri aramak için kullanılan bir yöntemdir. Grafik geçişi, düğüm düzenlemesi için kullanılan sıraya karar vermek için kullanılır. Ayrıca, bir döngü oluşturmadan kenarları arar, yani tüm düğümler ve kenarlar bir döngü oluşturmadan aranabilir.

İki grafik geçiş yapısı vardır.

1. DFS (Önce Derinlik Arama): Derinlemesine arama yöntemi

DFS araması, ilk düğümden başlayarak başlar ve daha derine iner ve hedeflenen düğüm bulunana kadar aşağıları keşfeder. Hedeflenen anahtar bulunamazsa, arama yolu, ilk arama sırasında keşfi durdurulan yola değiştirilir ve aynı prosedür o dal için tekrarlanır.

Yayılan ağaç, bu aramanın sonucundan üretilir. Bu ağaç yöntemi döngüler olmadan. DFS geçişini uygulamak için yığın veri yapısındaki toplam düğüm sayısı kullanılır.

DFS aramasını uygulamak için izlenen adımlar:

Adım 1 – Yığın boyutu, toplam düğüm sayısına bağlı olarak tanımlanmalıdır.

Adım 2 – Çapraz için ilk düğümü seçin; o düğümü ziyaret ederek yığına itilmesi gerekiyor.

Adım 3 – Şimdi, daha önce ziyaret edilmeyen bitişik düğümü ziyaret edin ve onu yığına itin.

Adım 4 – Ziyaret edilmeyen bitişik düğüm kalmayana kadar Adım 3'ü tekrarlayın.

Adım 5 – Ziyaret edilecek başka düğüm olmadığında geri izlemeyi ve bir düğümü kullanın.

Adım 6 – 3,4 ve 5 numaralı adımları tekrarlayarak yığını boşaltın.

Adım 7 – Yığın boş olduğunda, kullanılmayan kenarlar elenerek son bir kapsayan ağaç oluşturulur.

DFS uygulamaları şunlardır:

• Bulmacaları tek bir çözümle çözmek.
• Bir grafiğin iki parçalı olup olmadığını test etmek için.
• İşi planlamak için Topolojik Sıralama ve diğerleri.

2. BFS (Genişlik-İlk Arama): Arama, bir kuyruğa alma yöntemi kullanılarak gerçekleştirilir

Genişlik-İlk Arama, bir grafikte genişlik hareketiyle gezinir ve yolda bir sonla karşılaştıktan sonra bir düğümden diğerine atlamak için Kuyruğa dayalı olarak kullanır.

BFS aramasını uygulamak için izlenen adımlar,

Adım 1 – Düğüm sayısına göre Kuyruk tanımlanır.

Adım 2 – Geçişin herhangi bir düğümünden başlayın. Bu düğümü ziyaret edin ve Kuyruğa ekleyin.

Adım 3 – Şimdi Kuyruğun önündeki ziyaret edilmeyen bitişik düğümü kontrol edin ve onu başlangıca değil Kuyruğa ekleyin.

Adım 4 – Şimdi ziyaret edilmesi gereken herhangi bir kenarı olmayan ve Kuyrukta olmayan düğümü silmeye başlayın.

Adım 5 – 4. ve 5. adımları tekrarlayarak Kuyruğu boşaltın.

Adım 6 – Kullanılmayan kenarları kaldırın ve yalnızca Kuyruk boşaldıktan sonra yayılan ağacı oluşturun.

BFS uygulamaları şunlardır:

• Eşler Arası Ağlar - Bittorrent'te olduğu gibi, tüm bitişik düğümleri bulmak için kullanılır.
• Arama Motorunda Tarayıcılar.
• Sosyal Ağ Web Siteleri ve daha fazlası.

Veri Yapısında Grafiğin Gerçek Dünya Uygulamaları

Grafikler, ağ gösterimi (yollar, fiber optik haritalama, devre kartı tasarımı vb.) gibi birçok günlük uygulamada kullanılır. Örn: Facebook veri ağında, düğümler kullanıcıyı, fotoğrafını veya yorumunu, kenarlar ise fotoğrafları, fotoğraftaki yorumları temsil eder.

Veri yapısındaki Grafik kapsamlı uygulamalara sahiptir. Dikkate değer olanlardan bazıları şunlardır:

• Sosyal Grafik API'leri – Verilerin Facebook sosyal medya platformu içinde ve dışında iletilmesinin birincil yoludur. Programlı olarak verileri sorgulamak, fotoğraf ve video yüklemek, yeni hikayeler oluşturmak ve diğer birçok görev için kullanılan HTTP tabanlı bir API'dir. Düğümler, kenarlar ve alanlardan oluşur; sorgulamak için belirli nesne düğümleri kullanılır. Tek bir nesneye maruz kalan bir grup nesne için kenarlar ve alanlar, grup içindeki her nesne hakkında veri getirmek için kullanılır.
• Yelp'in GraphQL API'si – Yelp platformundan belirli verileri getirmek için kullanılan bir öneri motorudur. Burada, kenarları bulmak için siparişler kullanılır, ardından kesin sonucu almak için belirli düğüm sorgulanır. Bu, geri alma sürecini hızlandırır.

Yelp platformunda düğümler, id, name, is_closed ve diğer birçok grafik özelliklerini içeren işi temsil eder.

• Yol Optimizasyon Algoritmaları- Hız, güvenlik, yakıt vb. kriterlere uyan en iyi bağlantıyı bulmak için kullanılırlar. Bu algoritmada BFS kullanılır. En iyi örnek Google Haritalar Platformudur (Haritalar, Rotalar API'leri).
• Uçuş Ağları - Uçuş ağlarında bu, grafik veri yapısına uyan optimize edilmiş yolu bulmak için kullanılır . Bu aynı zamanda modele yardımcı olur ve havalimanı prosedürlerini verimli bir şekilde optimize eder.

Ayrıca Okuyun: Veri Görselleştirmenin Faydaları

Çözüm

Bu yazımızda önce Grafik ve Grafiğin veri yapısındaki tanımını ele aldık ve ardından grafik çeşitlerini özellikleriyle birlikte öğrendik. Daha sonra, grafiklerin depolanması için yaygın olarak kullanılan yöntemleri ve ardından Grafikler, Grafik Geçişinde kullanılan önemli konu arama yöntemlerini öğrendik. Son olarak, grafik veri yapısının gerçek dünyadaki uygulamalarını tartıştık.

Bu makale , veri yapısındaki Grafikler hakkında bilgi sağlamıştır ; Bunun bilgisi, Graph veritabanlarında, arama algoritması uygulamasında, programlamada ve daha birçok konuda temel anlayış için hayati önem taşır. Endüstri uzmanından öğrenilmelidir.

Neden upGrad ile bir Kurs Seçmelisiniz ?

UpGrad'da barındırılan IIIT Bangalore tarafından sunulan Veri Biliminde Yönetici PG Programını seçmenizi öneririz çünkü burada kurs eğitmenleriyle 1-1 sorgularınızı alabilirsiniz. Sadece teorik öğrenmeye odaklanmakla kalmaz, aynı zamanda öğrencileri gerçek dünya projeleriyle yüzleşmeye hazırlamak için gerekli olan ve size Veri Biliminde yüksek ücretli işler almanıza yardımcı olan Hindistan'ın 1. NASSCOM sertifikasını sağlayan pratik temelli bilgiye önem verir.

Alıntılanan Eserler

Matematik Bölümü/CS – Ana Sayfa , www.mathcs.emory.edu/~cheung/Courses/171/Syllabus/11-Graph/data-stru.html.

"Matematik Anlayışı." Yönlendirilmiş Grafik Tanımı – Math Insight , matinsight.org/definition/directed_graph.

Singh, Amritpal. "Grafik Veri Yapısı." Medium , Medium, 29 Mart 2020, medium.com/@singhamritpal49/graph-data-structure-49427c81b3b3.

Solo. “Bilmeniz Gereken Grafik Veri Yapılarının Gerçek Hayat Uygulamaları.” Graph Data ve GraphQL API Development-Leap Graph , leapgraph.com/graph-data-structures-applications.