Grafice în structura datelor: tipuri, stocare și traversare

O structură de date este o modalitate eficientă de organizare a datelor în știința datelor, astfel încât acele date să poată fi accesate cu ușurință și utilizate în mod eficient. Există multe tipuri de baze de date, dar motivul pentru care graficele joacă un rol vital în gestionarea datelor este discutat în acest articol.

Alertă spoiler: utilizați în fiecare zi Graphs în structura de date pentru a obține cea mai bună rută către birou, pentru a obține sugestii pentru prânz, film și pentru a optimiza următoarea rută de zbor. Sună interesant! Să vedem despre proprietățile graficului și aplicația acestuia.

Mai întâi, să vedem ce este un grafic? Este o reprezentare a datelor într-o structură neliniară constând din noduri (sau vârfuri) și muchii (sau căi).

Un grafic din structura de date poate fi numit ca o structură de date constând din date care sunt stocate între multe grupuri de muchii (căi) și vârfuri (noduri), care sunt interconectate. Structura datelor grafice (N, E) este structurată cu o colecție de noduri și margini. Atât nodurile, cât și vârfurile trebuie să fie finite.

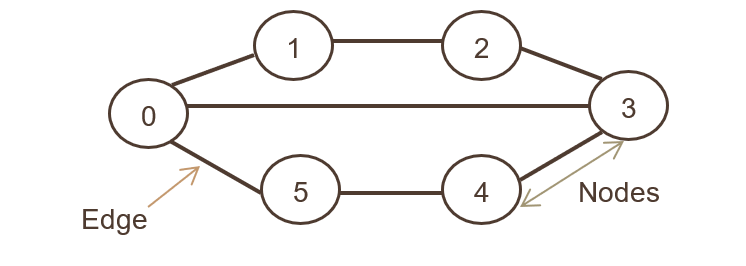
În reprezentarea grafică de mai sus, setul de noduri sunt N={0,1,2,3,4,5,6}și setul de muchii sunt

G={01,12,23,34,45,05,03}

Acum să studiem tipurile de grafice.

Citiți: Top 10 tehnici de vizualizare a datelor

Tipuri de grafice

1. Grafic ponderat

Grafice ale căror margini sau trasee au valori. Toate valorile văzute asociate cu marginile se numesc greutăți. Valoarea marginilor poate reprezenta greutatea/costul/lungimea.

Valorile sau ponderile pot reprezenta, de asemenea:

• Distanța acoperită între două puncte - De exemplu: pentru a căuta cea mai scurtă cale către birou, distanța dintre două stații de lucru dintr-o rețea de birouri.
• Viteza pachetului de date într-o rețea sau lățimea de bandă.

2. Grafic neponderat

Acolo unde nu există nicio valoare sau greutate asociată cu marginea. În mod implicit, toate graficele sunt neponderate, cu excepția cazului în care există o valoare asociată.

3. Grafic nedirecționat

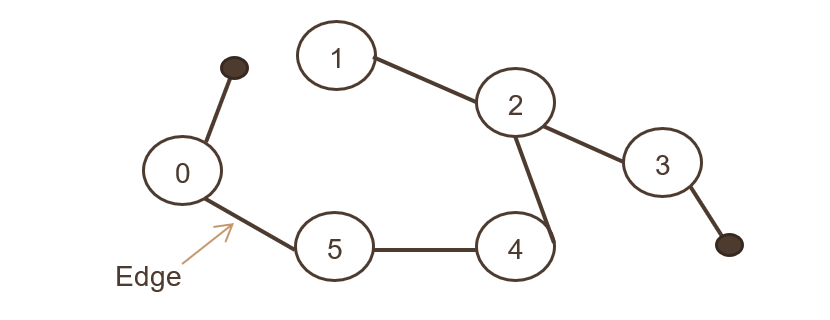
Unde un set de obiecte este conectat și toate marginile sunt bidirecționale. Imaginea de mai jos prezintă graficul nedirecționat,

Este ca asociativitatea a doi utilizatori Facebook după conectarea ca prieten. Ambii utilizatori pot trimite și partaja fotografii, comenta între ei.

4. Graficul Dirijat

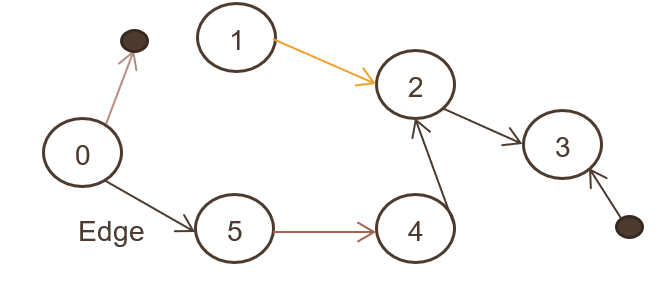
Denumit și digraf, unde un set de obiecte (N, E) sunt conectate, iar toate marginile sunt direcționate de la un nod la altul. Imaginea de mai sus prezintă graficul direcționat.

Checkout: Proiecte de vizualizare a datelor pe care le puteți replica

Stocarea graficului

Fiecare metodă de stocare are avantajele și dezavantajele sale, iar metoda de stocare potrivită este aleasă în funcție de complexitate. Cele mai utilizate două structuri de date pentru stocarea graficelor sunt:

1. Lista adiacentei

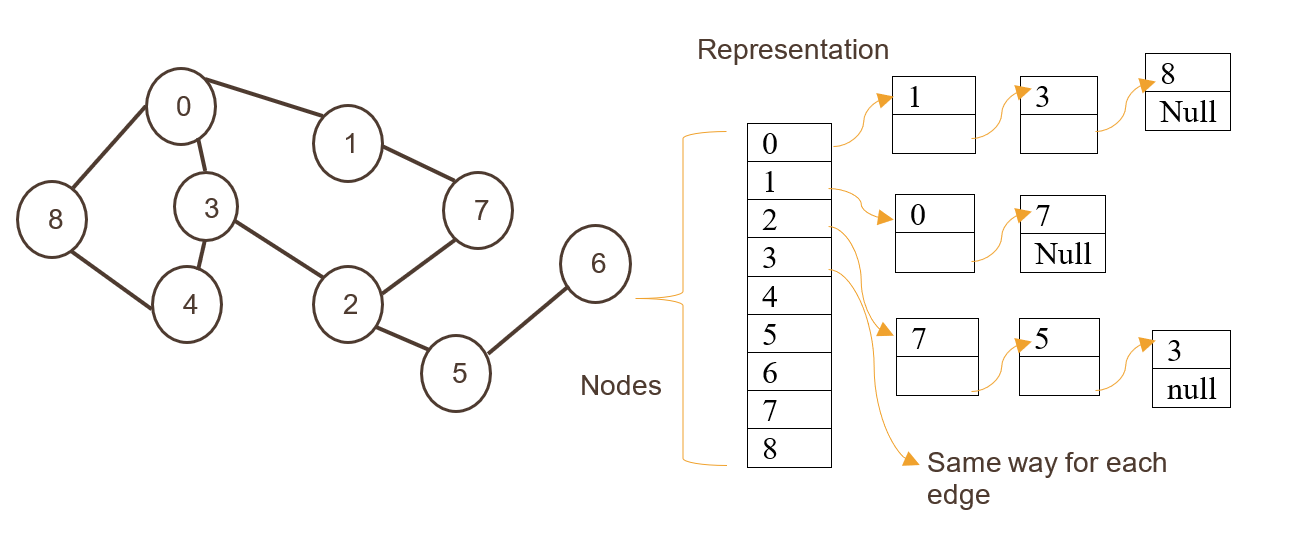
Aici nodurile sunt stocate ca un index al matricei unidimensionale, urmat de marginile stocate ca o listă.

2. Matricea adiacentei

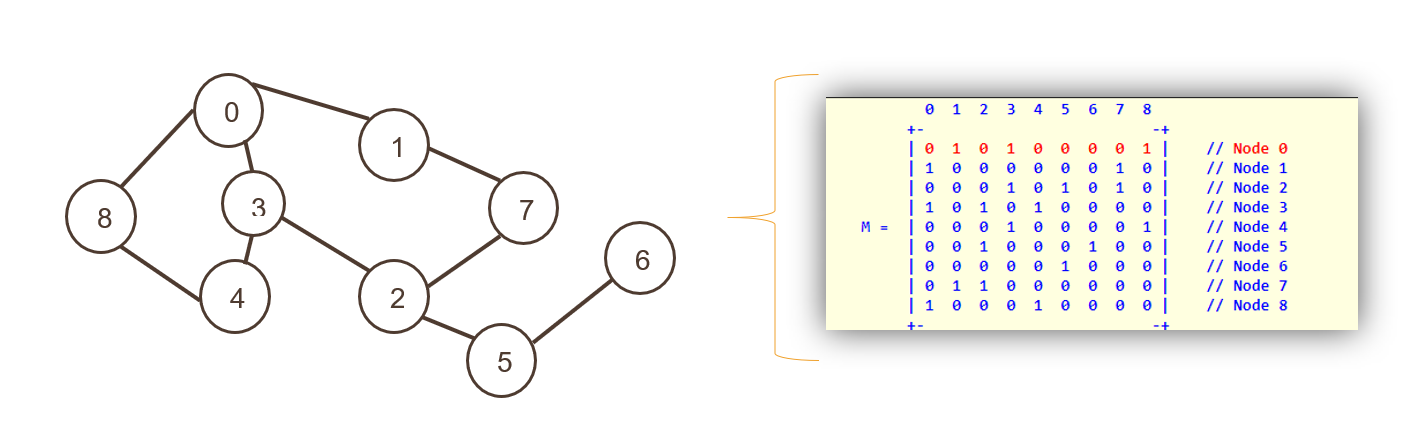
Aici nodurile sunt reprezentate ca indicele unei matrice bidimensionale, urmate de marginile reprezentate ca valori diferite de zero ale unei matrice adiacente.

Atât rândurile, cât și coloanele prezintă Noduri; întreaga matrice este umplută fie cu „0”, fie cu „1”, reprezentând adevărat sau fals. Zero înseamnă că nu există o cale, iar 1 reprezintă o cale.

Traversarea graficului

Graph traversal este o metodă folosită pentru a căuta noduri într-un grafic. Traversarea graficului este folosită pentru a decide ordinea folosită pentru aranjarea nodurilor. De asemenea, caută margini fără a face o buclă, ceea ce înseamnă că toate nodurile și marginile pot fi căutate fără a crea o buclă.

Există două structuri de traversare a graficului.

1. DFS (Depth First Search): Metodă de căutare aprofundată

Căutarea DFS începe pornind de la primul nod și merge din ce în ce mai adânc, explorând în jos până când este găsit nodul vizat. Dacă cheia vizată nu este găsită, calea de căutare este schimbată la calea care a fost oprită în explorarea în timpul căutării inițiale și aceeași procedură se repetă pentru acea ramură.

Arborele spanning este produs din rezultatul acestei căutări. Această metodă de arbore este fără bucle. Numărul total de noduri din structura de date a stivei este utilizat pentru a implementa traversarea DFS.

Pașii urmați pentru implementarea căutării DFS:

Pasul 1 – Dimensiunea stivei trebuie definită în funcție de numărul total de noduri.

Pasul 2 – Selectați nodul inițial pentru transversal; trebuie să fie împins în stivă vizitând acel nod.

Pasul 3 – Acum, vizitați nodul adiacent care nu a fost vizitat înainte și împingeți-l în stivă.

Pasul 4 – Repetați pasul 3 până când nu există niciun nod adiacent care să nu fie vizitat.

Pasul 5 – Folosiți backtracking și un nod atunci când nu există alte noduri de vizitat.

Pasul 6 - Goliți stiva repetând pașii 3, 4 și 5.

Pasul 7 – Când stiva este goală, se formează un arbore de acoperire final prin eliminarea marginilor nefolosite.

Aplicațiile DFS sunt:

• Rezolvarea puzzle-urilor cu o singură soluție.
• Pentru a testa dacă un grafic este bipartit.
• Sortare topologică pentru programarea jobului și multe altele.

2. BFS (Breadth-First Search): Căutarea este implementată folosind o metodă de așteptare

Breadth-First Search navighează într-un grafic într-o mișcare de lățime și utilizează pe baza Cozii pentru a sări de la un nod la altul, după ce a întâlnit un capăt în cale.

Pașii urmați pentru implementarea căutării BFS,

Pasul 1 – Pe baza numărului de noduri, coada este definită.

Pasul 2 – Începeți de la orice nod al traversării. Vizitați acel nod și adăugați-l la coadă.

Pasul 3 - Acum verificați nodul adiacent nevizitat, care se află în fața Cozii și adăugați-l în Coadă, nu la început.

Pasul 4 – Acum începeți să ștergeți nodul care nu are margini care trebuie vizitate și nu se află în coadă.

Pasul 5 - Goliți coada repetând pașii 4 și 5.

Pasul 6 – Îndepărtați marginile nefolosite și formați arborele de întindere numai după ce coada este goală.

Aplicațiile BFS sunt:

• Rețele Peer-to-Peer - Ca și în Bittorrent, este folosit pentru a găsi toate nodurile adiacente.
• Crawlerele în motorul de căutare.
• Site-uri de rețele sociale și multe altele.

Aplicații reale ale graficului în structura datelor

Graficele sunt utilizate în multe aplicații de zi cu zi, cum ar fi reprezentarea rețelei (drumuri, cartografierea fibrei optice, proiectarea plăcilor de circuite etc.). Ex: În rețeaua de date Facebook, nodurile reprezintă utilizatorul, fotografia sau comentariul acestuia, iar marginile reprezintă fotografii, comentarii la fotografie.

Graficul din structura datelor are aplicații extinse. Unele dintre cele notabile sunt:

• API-uri Social Graph – Este modalitatea principală prin care datele sunt comunicate în și în afara platformei de socializare Facebook. Este un API bazat pe HTTP, care este folosit pentru a interoga în mod programatic date, pentru a încărca fotografii și videoclipuri, pentru a crea povești noi și pentru multe alte sarcini. Este compus din noduri, margini și câmpuri; pentru a interoga, sunt folosite nodurile obiect specifice. Marginile pentru un grup de obiecte supuse unui singur obiect și câmpurile sunt folosite pentru a prelua date despre fiecare obiect din grup.
• API-ul GraphQL Yelp – Este un motor de recomandare folosit pentru a prelua datele specifice de pe platforma Yelp. Aici, comenzile sunt folosite pentru a găsi marginile, după care nodul specific este interogat pentru a obține rezultatul exact. Acest lucru accelerează procesul de recuperare.

Pe platforma Yelp, nodurile reprezintă afacerea, conținând id, nume, is_closed și multe alte proprietăți grafice.

• Algoritmi de optimizare a traseului - Aceștia sunt utilizați pentru a găsi cea mai bună conexiune care se potrivește criteriilor de viteză, siguranță, combustibil etc. BFS este utilizat în acest algoritm. Cel mai bun exemplu este Google Maps Platform (API-uri Maps, Routes).
• Rețele de zbor - În rețelele de zbor, aceasta este utilizată pentru a găsi calea optimizată care se potrivește structurii de date grafice . Acest lucru ajută, de asemenea, la model și optimizează eficient procedurile aeroportuare.

Citiți și: Beneficiile vizualizării datelor

Concluzie

În acest articol, am discutat mai întâi despre definiția Graph și Graph în structura datelor și apoi am învățat despre tipurile de grafice cu proprietățile lor. Mai târziu, am aflat despre metodele utilizate în mod obișnuit pentru stocarea graficelor, urmate de metode importante de căutare a subiectelor utilizate în Graphs, Graph Traversal. În cele din urmă, am discutat despre aplicațiile din lumea reală ale structurii datelor grafice.

Acest articol a oferit o perspectivă asupra graficelor din structura datelor ; cunoașterea acestui lucru este vitală pentru înțelegerea fundamentală în bazele de date Graph, implementarea algoritmului de căutare, programare și multe altele. Trebuie învățat de la expertul din industrie.

De ce să alegeți un curs cu upGrad ?

Vă recomandăm să alegeți Programul Executive PG în Data Science oferit de IIIT Bangalore găzduit pe upGrad, deoarece aici puteți obține întrebările dvs. 1-1 cu instructorii cursului. Nu se concentrează doar pe învățarea teoretică, ci acordă importanță cunoștințelor practice, care sunt esențiale pentru a pregăti cursanții pentru proiecte din lumea reală și pentru a vă oferi primul certificat NASSCOM din India, care vă ajută să obțineți locuri de muncă bine plătite în știința datelor.

Lucrari citate

Departamentul de Matematică/CS – Acasă , www.mathcs.emory.edu/~cheung/Courses/171/Syllabus/11-Graph/data-stru.html.

„Perspectivă matematică”. Directed Graph Definition – Math Insight , mathinsight.org/definition/directed_graph.

Singh, Amritpal. „Structura datelor grafice”. Mediu , Mediu, 29 martie 2020, medium.com/@singhamritpal49/graph-data-structure-49427c81b3b3.

Solo. „Aplicațiile din viața reală ale structurilor de date grafice pe care trebuie să le cunoașteți.” Graph Data și GraphQL API Development-Leap Graph , leapgraph.com/graph-data-structures-applications.