Graphiques dans la structure de données : types, stockage et parcours

Une structure de données est un moyen efficace d'organiser les données en science des données afin que ces données soient facilement accessibles et utilisées efficacement. Il existe de nombreux types de bases de données, mais cet article explique pourquoi les graphiques jouent un rôle vital dans la gestion des données.

Alerte spoiler : vous utilisez quotidiennement Graphs dans la structure des données pour rechercher le meilleur itinéraire jusqu'à votre bureau, pour obtenir des suggestions pour votre déjeuner, votre film et pour optimiser votre prochain itinéraire de vol. Ça semble intéressant! Voyons les propriétés du graphe et son application.

Voyons d'abord ce qu'est un graphe ? C'est une représentation des données dans une structure non linéaire composée de nœuds (ou sommets) et d'arêtes (ou chemins).

Un graphe dans la structure de données peut être qualifié de structure de données constituée de données stockées parmi de nombreux groupes d'arêtes (chemins) et de sommets (nœuds), qui sont interconnectés. La structure de données du graphe (N, E) est structurée avec une collection de nœuds et d'arêtes. Les nœuds et les sommets doivent être finis.

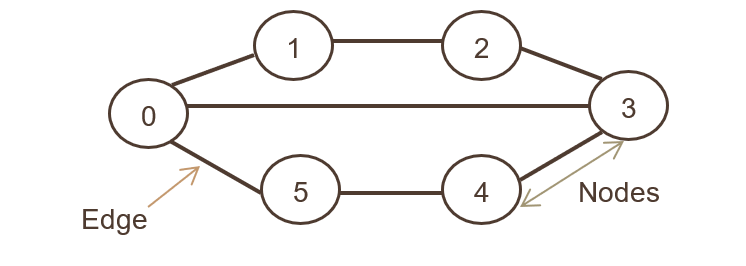
Dans la représentation graphique ci-dessus, l'ensemble des nœuds est N={0,1,2,3,4,5,6} et l'ensemble des arêtes est

G={01,12,23,34,45,05,03}

Étudions maintenant les types de graphes.

Lire : Top 10 des techniques de visualisation de données

Types de graphiques

1. Graphique pondéré

Graphiques dont les arêtes ou les chemins ont des valeurs. Toutes les valeurs vues associées aux arêtes sont appelées poids. La valeur des bords peut représenter le poids/coût/longueur.

Les valeurs ou les poids peuvent également représenter :

• Distance parcourue entre deux points - Ex : Pour rechercher le chemin le plus court vers le bureau, la distance entre deux postes de travail dans un réseau de bureau.
• Vitesse du paquet de données dans un réseau ou bande passante.

2. Graphique non pondéré

Où il n'y a pas de valeur ou de poids associé à l'arête. Par défaut, tous les graphiques sont non pondérés sauf s'il y a une valeur associée.

3. Graphe non orienté

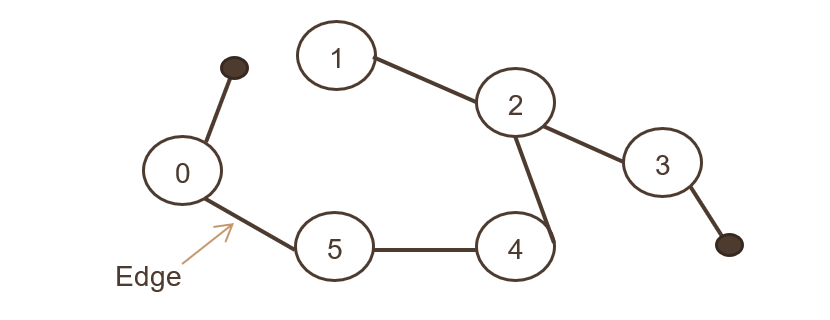
Où un ensemble d'objets sont connectés, et tous les bords sont bidirectionnels. L'image ci-dessous présente le graphique non orienté,

C'est comme l'associativité de deux utilisateurs de Facebook après s'être connectés en tant qu'ami. Les deux utilisateurs peuvent se référer et partager des photos, commenter entre eux.

4. Graphe orienté

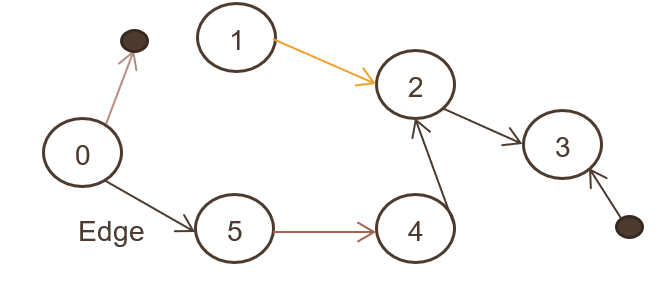
Aussi appelé un digraphe, où un ensemble d'objets (N, E) sont connectés, et toutes les arêtes sont dirigées d'un nœud à l'autre. L'image ci-dessus présente le graphique orienté.

Checkout : Projets de visualisation de données que vous pouvez répliquer

Stockage du graphique

Chaque méthode de stockage a ses avantages et ses inconvénients, et la bonne méthode de stockage est choisie en fonction de la complexité. Les deux structures de données les plus couramment utilisées pour stocker des graphiques sont :

1. Liste de contiguïté

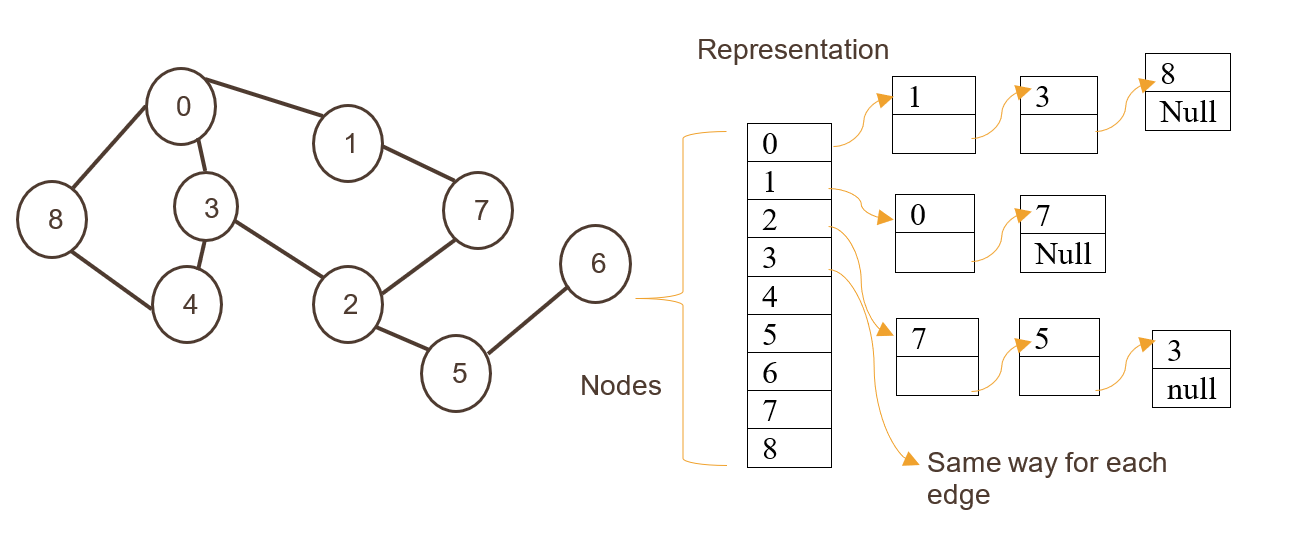
Ici, les nœuds sont stockés sous la forme d'un index du tableau à une dimension suivi des arêtes stockées sous forme de liste.

2. Matrice de contiguïté

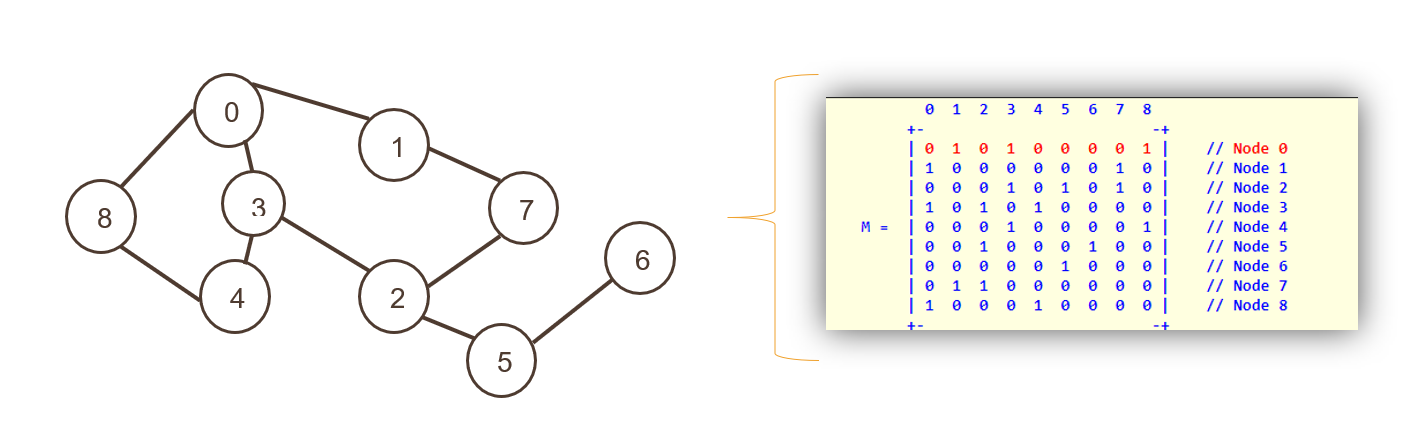
Ici, les nœuds sont représentés comme l'indice d'un tableau à deux dimensions, suivi des arêtes représentées comme des valeurs non nulles d'une matrice adjacente.

Les lignes et les colonnes présentent les nœuds ; la matrice entière est remplie de "0" ou de "1", représentant vrai ou faux. Zéro signifie qu'il n'y a pas de chemin et 1 représente un chemin.

Traversée de graphe

La traversée de graphe est une méthode utilisée pour rechercher des nœuds dans un graphe. Le parcours du graphe est utilisé pour décider de l'ordre utilisé pour l'arrangement des nœuds. Il recherche également les arêtes sans faire de boucle, ce qui signifie que tous les nœuds et arêtes peuvent être recherchés sans créer de boucle.

Il existe deux structures de parcours de graphe.

1. DFS (Depth First Search) : méthode de recherche approfondie

La recherche DFS commence à partir du premier nœud et va de plus en plus loin, explorant jusqu'à ce que le nœud ciblé soit trouvé. Si la clé ciblée n'est pas trouvée, le chemin de recherche est remplacé par le chemin qui a été arrêté d'explorer lors de la recherche initiale, et la même procédure est répétée pour cette branche.

L'arbre couvrant est produit à partir du résultat de cette recherche. Cette méthode arborescente est sans les boucles. Le nombre total de nœuds dans la structure de données de la pile est utilisé pour implémenter la traversée DFS.

Étapes suivies pour implémenter la recherche DFS :

Étape 1 - La taille de la pile doit être définie en fonction du nombre total de nœuds.

Étape 2 - Sélectionnez le nœud initial pour le transversal ; il doit être poussé vers la pile en visitant ce nœud.

Étape 3 - Maintenant, visitez le nœud adjacent qui n'a pas été visité auparavant et poussez-le vers la pile.

Étape 4 – Répétez l'étape 3 jusqu'à ce qu'il n'y ait plus de nœud adjacent non visité.

Étape 5 - Utilisez le retour en arrière et un nœud lorsqu'il n'y a pas d'autres nœuds à visiter.

Étape 6 – Videz la pile en répétant les étapes 3, 4 et 5.

Étape 7 - Lorsque la pile est vide, un arbre couvrant final est formé en éliminant les arêtes inutilisées.

Les applications de DFS sont :

• Résoudre des énigmes avec une seule solution.
• Tester si un graphe est biparti.
• Tri topologique pour planifier le travail et bien d'autres.

2. BFS (Breadth-First Search) : la recherche est mise en œuvre à l'aide d'une méthode de mise en file d'attente

La recherche en largeur d'abord navigue dans un graphique dans un mouvement de largeur et utilise la file d'attente pour passer d'un nœud à un autre, après avoir rencontré une fin dans le chemin.

Étapes suivies pour mettre en œuvre la recherche BFS,

Étape 1 – En fonction du nombre de nœuds, la file d'attente est définie.

Étape 2 - Commencez à partir de n'importe quel nœud de la traversée. Visitez ce nœud et ajoutez-le à la file d'attente.

Étape 3 - Vérifiez maintenant le nœud adjacent non visité, qui se trouve devant la file d'attente, et ajoutez-le dans la file d'attente, pas au début.

Étape 4 - Commencez maintenant à supprimer le nœud qui n'a pas de bords à visiter et qui n'est pas dans la file d'attente.

Étape 5 – Videz la file d'attente en répétant les étapes 4 et 5.

Étape 6 - Supprimez les bords inutilisés et formez l'arbre couvrant uniquement après que la file d'attente est vide.

Les applications de BFS sont :

• Réseaux Peer to Peer - Comme dans Bittorrent, il est utilisé pour trouver tous les nœuds adjacents.
• Crawlers dans le moteur de recherche.
• Sites Web de réseautage social et bien d'autres.

Applications réelles du graphe dans la structure de données

Les graphes sont utilisés dans de nombreuses applications courantes comme la représentation de réseaux (routes, cartographie des fibres optiques, conception de circuits imprimés, etc.). Ex : Dans le réseau de données Facebook, les nœuds représentent l'utilisateur, sa photo ou son commentaire, et les bords représentent des photos, des commentaires sur la photo.

Le graphe dans la structure de données a de nombreuses applications. Certains des notables sont:

• API Social Graph - C'est la principale façon dont les données sont communiquées dans et hors de la plate-forme de médias sociaux Facebook. Il s'agit d'une API basée sur HTTP, qui est utilisée pour interroger des données par programmation, télécharger des photos et des vidéos, créer de nouvelles histoires et bien d'autres tâches. Il est composé de nœuds, d'arêtes et de champs ; pour interroger, les nœuds d'objet spécifiques sont utilisés. Les bords d'un groupe d'objets soumis à un seul objet et les champs sont utilisés pour extraire des données sur chaque objet du groupe.
• API GraphQL de Yelp - Il s'agit d'un moteur de recommandation utilisé pour récupérer les données spécifiques de la plate-forme Yelp. Ici, les ordres sont utilisés pour trouver les arêtes, après quoi le nœud spécifique est interrogé pour récupérer le résultat exact. Cela accélère le processus de récupération.

Sur la plate-forme Yelp, les nœuds représentent l'entreprise, contenant l'identifiant, le nom, is_closed et de nombreuses autres propriétés de graphique.

• Algorithmes d'optimisation de chemin - Ils sont utilisés pour trouver la meilleure connexion qui correspond aux critères de vitesse, de sécurité, de carburant, etc. BFS est utilisé dans cet algorithme. Le meilleur exemple est Google Maps Platform (Maps, Routes APIs).
• Réseaux de vol - Dans les réseaux de vol, ceci est utilisé pour trouver le chemin optimisé qui correspond à la structure de données du graphique . Cela facilite également le modèle et optimise efficacement les procédures aéroportuaires.

A lire également : Avantages de la visualisation des données

Conclusion

Dans cet article, nous avons d'abord discuté de la définition de graphe et de graphe dans la structure de données, puis nous avons découvert les types de graphes avec leurs propriétés. Plus tard, nous avons découvert les méthodes couramment utilisées pour le stockage des graphes, suivies des méthodes de recherche de sujets importantes utilisées dans Graphs, Graph Traversal. Enfin, nous avons discuté des applications réelles de la structure de données de graphe.

Cet article a fourni un aperçu sur les graphes dans la structure de données ; la connaissance de cela est essentielle pour la compréhension fondamentale des bases de données Graph, de la mise en œuvre des algorithmes de recherche, de la programmation et bien d'autres. Il doit être appris de l'expert de l'industrie.

Pourquoi choisir un cours avec upGrad ?

Nous vous recommandons de choisir le programme Executive PG en science des données proposé par IIIT Bangalore hébergé sur upGrad car ici, vous pouvez obtenir vos questions 1-1 avec les instructeurs du cours. Il ne se concentre pas uniquement sur l'apprentissage théorique, mais accorde de l'importance aux connaissances pratiques, qui sont essentielles pour préparer les apprenants à faire face à des projets du monde réel et vous fournir le premier certificat indien NASSCOM, qui vous aide à obtenir des emplois bien rémunérés en science des données.

Ouvrages cités

Département de mathématiques/CS – Accueil , www.mathcs.emory.edu/~cheung/Courses/171/Syllabus/11-Graph/data-stru.html.

"Conseil mathématique". Définition de graphe orienté - Math Insight , mathinsight.org/definition/directed_graph.

Singh, Amritpal. "Structure de données de graphique." Medium , Medium, 29 mars 2020, medium.com/@singhamritpal49/graph-data-structure-49427c81b3b3.

Solo. "Les applications réelles des structures de données graphiques que vous devez connaître." Développement de données graphiques et d'API GraphQL - Leap Graph , leapgraph.com/graph-data-structures-applications.