你需要知道的 6 種神經網絡中的激活函數

隨著深度學習成為主流技術，最近有很多關於 ANN 或人工神經網絡的討論。 如今，人工神經網絡已成為各種新興領域的核心組件，例如手寫識別、圖像壓縮、股票交易預測等等。 閱讀有關機器學習中人工神經網絡類型的更多信息。

但什麼是人工神經網絡？

人工神經網絡是一種深度學習模型，它從人腦的神經結構中汲取靈感。 人工神經網絡的設計目的是模仿人類大腦從經驗中學習並相應地適應情況的功能。 就像人腦有一個包含數十億個按層次排列的神經元的多層結構一樣，人工神經網絡也有一個神經元網絡，這些神經元通過軸突相互連接。

這些相互連接的神經元將電信號（稱為突觸）從一層傳遞到另一層。 這種對大腦建模的模仿允許人工神經網絡從經驗中學習，而無需人工干預。

閱讀：數據挖掘中的人工神經網絡

因此，人工神經網絡是複雜的結構，包含相互關聯的自適應元素，稱為人工神經元，可以為知識表示執行大量計算。 它們具有生物神經元系統的所有基本品質，包括學習能力、魯棒性、非線性、高並行性、容錯性、處理不精確和模糊信息的能力以及泛化能力。

加入來自世界頂級大學的在線人工智能課程——碩士、高管研究生課程和 ML 和 AI 高級證書課程，以加快您的職業生涯。

人工神經網絡的核心特徵

• 非線性賦予數據更好的擬合度。
• 高並行性促進了快速處理和硬件​​故障容錯。
• 泛化允許將模型應用於未學習的數據。
• 對噪聲不敏感，即使對於不確定的數據和測量誤差也能進行準確的預測。
• 學習和適應性允許模型根據不斷變化的環境更新其內部架構。

基於人工神經網絡的計算主要旨在設計先進的數學算法，使人工神經網絡能夠通過模仿人腦的信息處理和知識獲取功能來學習。

人工神經網絡的組成部分

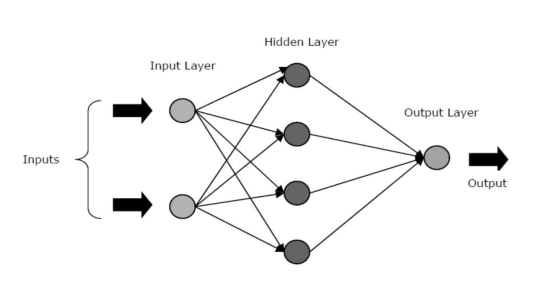
人工神經網絡由三個核心層或階段組成——輸入層、隱藏層和輸出層。

• 輸入層：第一層輸入輸入，即原始數據。 它將來自外界的信息傳遞到網絡。 在這一層中，不執行任何計算——節點只是將信息傳遞給隱藏層。
• 隱藏層：在這一層中，節點隱藏在輸入層後面——它們構成了每個神經網絡中的抽象部分。 通過輸入層輸入的特徵的所有計算都發生在隱藏層中，然後，它將結果傳輸到輸出層。
• 輸出層：該層描述了網絡對外部世界執行的計算結果。

資源

神經網絡可以根據隱藏層的活動分為不同的類型。 例如，在一個簡單的神經網絡中，隱藏單元可以構建它們對輸入的唯一表示。 在這裡，隱藏單元和輸入單元之間的權重決定了每個隱藏單元何時處於活動狀態。

因此，通過調整這些權重，隱藏層可以選擇它應該表示的內容。 其他架構包括單層和多層模型。 在單層中，通常只有輸入和輸出層——它沒有隱藏層。 而在多層模型中，有一個或多個隱藏層。

什麼是神經網絡中的激活函數？

正如我們之前提到的，人工神經網絡是許多有助於徹底改變我們周圍世界的結構的重要組成部分。 但是你有沒有想過，人工神經網絡如何提供最先進的性能來找到現實問題的解決方案？

答案是——激活函數。

ANN 使用激活函數 (AF) 在隱藏層中執行複雜的計算，然後將結果傳輸到輸出層。 AFs 的主要目的是在神經網絡中引入非線性特性。

它們將節點的線性輸入信號轉換為非線性輸出信號，以促進對深度網絡超過一階的高階多項式的學習。 AF 的一個獨特方面是它們是可微的——這有助於它們在神經網絡的反向傳播過程中發揮作用。

需要什麼非線性？

如果不應用激活函數，則輸出信號將是一個線性函數，它是一次多項式。 雖然求解線性方程很容易，但它們的複雜度商有限，因此從數據中學習複雜函數映射的能力較小。 因此，如果沒有 AF，神經網絡將是一個能力有限的線性回歸模型。

這當然不是我們想要的神經網絡。 神經網絡的任務是計算高度複雜的計算。 此外，沒有 AF，神經網絡無法學習和建模其他復雜數據，包括圖像、語音、視頻、音頻等。

AF 幫助神經網絡理解具有復雜架構的複雜、高維和非線性的大數據集——它們在輸入和輸出層之間包含多個隱藏層。

閱讀：深度學習與神經網絡

現在，事不宜遲，讓我們深入了解 ANN 中使用的不同類型的激活函數。

激活函數的類型

1. Sigmoid 函數

在 ANN 中，sigmoid 函數是一種非線性 AF，主要用於前饋神經網絡。 它是一個可微的實函數，為實輸入值定義，並且在任何地方都包含具有特定平滑度的正導數。 sigmoid 函數出現在深度學習模型的輸出層，用於預測基於概率的輸出。 sigmoid 函數表示為：

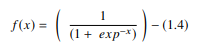
資源

通常，sigmoid 函數的導數被應用於學習算法。 sigmoid 函數的圖形是“S”形的。

sigmoid 函數的一些主要缺點包括梯度飽和、收斂緩慢、從更深的隱藏層到輸入層的反向傳播過程中的陡峭阻尼梯度，以及導致梯度更新在不同方向上傳播的非零中心輸出。

2.雙曲正切函數（Tanh）

雙曲正切函數，又名 tanh 函數，是另一種類型的 AF。 它是一個更平滑、以零為中心的函數，範圍在 -1 到 1 之間。因此，tanh 函數的輸出表示為：

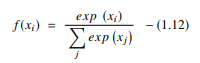
資源

tanh 函數比 sigmoid 函數使用更廣泛，因為它為多層神經網絡提供了更好的訓練性能。 tanh 函數的最大優點是它產生一個以零為中心的輸出，從而支持反向傳播過程。 tanh 函數主要用於自然語言處理和語音識別任務的循環神經網絡。

但是，tanh 函數也有一個局限性——就像 sigmoid 函數一樣，它不能解決梯度消失問題。 此外，當輸入值為 0（x 為零）時，tanh 函數只能獲得 1 的梯度。 結果，該函數在計算過程中會產生一些死神經元。

3.Softmax函數

softmax 函數是另一種用於神經網絡的 AF，用於從實數向量計算概率分佈。 該函數生成一個介於 0 和 1 之間且概率之和等於 1 的輸出。softmax 函數表示如下：

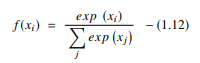
資源

該函數主要用於多類模型，它返回每個類的概率，目標類的概率最高。 它出現在幾乎所有使用它們的 DL 架構的輸出層中。 sigmoid 和 softmax AF 的主要區別在於前者用於二元分類，後者用於多變量分類。

4.軟簽功能

softsign 函數是另一種用於神經網絡計算的 AF。 雖然它主要用於回歸計算問題，但現在它也用於基於 DL 的文本到語音應用程序。 它是一個二次多項式，表示為：

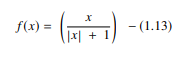
資源

這裡“x”等於輸入的絕對值。

softsign 函數和 tanh 函數的主要區別在於，與 tanh 函數以指數方式收斂不同，softsign 函數以多項式形式收斂。

5. 整流線性單元（ReLU）函數

DL 模型中最受歡迎的 AF 之一是整流線性單元 (ReLU) 函數，它是一種快速學習的 AF，有望提供最先進的性能和出色的結果。 與 sigmoid 和 tanh 函數等其他 AF 相比，ReLU 函數在深度學習中提供了更好的性能和泛化能力。 該函數是一個近乎線性的函數，保留了線性模型的特性，這使得它們易於使用梯度下降方法進行優化。

ReLU 函數對每個輸入元素執行閾值操作，其中所有小於零的值都設置為零。 因此，ReLU 表示為：

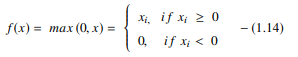
資源

通過糾正小於零的輸入值並將其設置為零，該函數消除了在早期類型的激活函數（sigmoid 和 tanh）中觀察到的梯度消失問題。

在計算中使用 ReLU 函數最顯著的優勢是它保證了更快的計算——它不計算指數和除法，從而提高了整體計算速度。 ReLU 函數的另一個關鍵方面是它通過壓縮零到最大值之間的值來在隱藏單元中引入稀疏性。

6. 指數線性單元 (ELU) 函數

指數線性單元 (ELU) 函數是一種 AF，也用於加速神經網絡的訓練（就像 ReLU 函數一樣）。 ELU 函數的最大優點是它可以通過對正值使用恆等以及通過改進模型的學習特性來消除梯度消失問題。

ELU 具有將平均單元激活推向零的負值，從而降低計算複雜度並提高學習速度。 ELU 是 ReLU 的絕佳替代品——它通過在訓練過程中將平均激活推向零來減少偏差。

指數線性單位函數表示為：

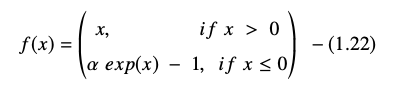
ELU 方程的導數或梯度表示為：

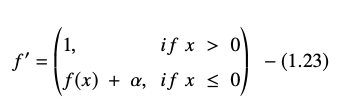
資源

這裡“α”等於控制負網絡輸入飽和點的 ELU 超參數，通常設置為 1.0。 但是，ELU 函數有一個限制——它不是以零為中心的。

結論

如今，像 ReLU 和 ELU 這樣的 AF 已經獲得了最大的關注，因為它們有助於消除梯度消失問題，該問題會在訓練過程中造成重大問題，並降低神經網絡模型的準確性和性能。

查看 IIT Madras 的機器學習和雲高級認證計劃，這是該國最好的工程學校，創建一個計劃，不僅可以教您機器學習，還可以使用雲基礎設施進行有效部署。 我們通過該計劃的目標是打開該國最具選擇性的學院的大門，並讓學習者獲得驚人的師資和資源，以掌握高增長的技能