你需要知道的 6 种神经网络中的激活函数

随着深度学习成为主流技术，最近有很多关于 ANN 或人工神经网络的讨论。 如今，人工神经网络已成为各种新兴领域的核心组件，例如手写识别、图像压缩、股票交易预测等等。 阅读有关机器学习中人工神经网络类型的更多信息。

但什么是人工神经网络？

人工神经网络是一种深度学习模型，它从人脑的神经结构中汲取灵感。 人工神经网络的设计目的是模仿人类大脑从经验中学习并相应地适应情况的功能。 就像人脑有一个包含数十亿个按层次排列的神经元的多层结构一样，人工神经网络也有一个神经元网络，这些神经元通过轴突相互连接。

这些相互连接的神经元将电信号（称为突触）从一层传递到另一层。 这种对大脑建模的模仿允许人工神经网络从经验中学习，而无需人工干预。

阅读：数据挖掘中的人工神经网络

因此，人工神经网络是复杂的结构，包含相互关联的自适应元素，称为人工神经元，可以为知识表示执行大量计算。 它们具有生物神经元系统的所有基本品质，包括学习能力、鲁棒性、非线性、高并行性、容错性、处理不精确和模糊信息的能力以及泛化能力。

加入来自世界顶级大学的在线人工智能课程——硕士、高管研究生课程和 ML 和 AI 高级证书课程，以加快您的职业生涯。

人工神经网络的核心特征

• 非线性赋予数据更好的拟合度。
• 高并行性促进了快速处理和硬件故障容错。
• 泛化允许将模型应用于未学习的数据。
• 对噪声不敏感，即使对于不确定的数据和测量误差也能进行准确的预测。
• 学习和适应性允许模型根据不断变化的环境更新其内部架构。

基于人工神经网络的计算主要旨在设计先进的数学算法，使人工神经网络能够通过模仿人脑的信息处理和知识获取功能来学习。

人工神经网络的组成部分

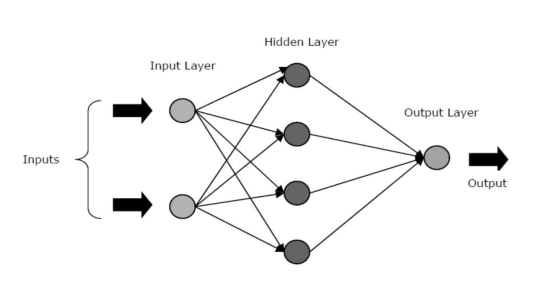
人工神经网络由三个核心层或阶段组成——输入层、隐藏层和输出层。

• 输入层：第一层输入输入，即原始数据。 它将来自外界的信息传递到网络。 在这一层中，不执行任何计算——节点只是将信息传递给隐藏层。
• 隐藏层：在这一层中，节点隐藏在输入层后面——它们构成了每个神经网络中的抽象部分。 通过输入层输入的特征的所有计算都发生在隐藏层中，然后，它将结果传输到输出层。
• 输出层：该层描述了网络对外部世界执行的计算结果。

资源

神经网络可以根据隐藏层的活动分为不同的类型。 例如，在一个简单的神经网络中，隐藏单元可以构建它们对输入的唯一表示。 在这里，隐藏单元和输入单元之间的权重决定了每个隐藏单元何时处于活动状态。

因此，通过调整这些权重，隐藏层可以选择它应该表示的内容。 其他架构包括单层和多层模型。 在单层中，通常只有输入和输出层——它没有隐藏层。 而在多层模型中，有一个或多个隐藏层。

什么是神经网络中的激活函数？

正如我们之前提到的，人工神经网络是许多有助于彻底改变我们周围世界的结构的重要组成部分。 但是你有没有想过，人工神经网络如何提供最先进的性能来找到现实问题的解决方案？

答案是——激活函数。

ANN 使用激活函数 (AF) 在隐藏层中执行复杂的计算，然后将结果传输到输出层。 AFs 的主要目的是在神经网络中引入非线性特性。

它们将节点的线性输入信号转换为非线性输出信号，以促进对深度网络超过一阶的高阶多项式的学习。 AF 的一个独特方面是它们是可微的——这有助于它们在神经网络的反向传播过程中发挥作用。

需要什么非线性？

如果不应用激活函数，则输出信号将是一个线性函数，它是一次多项式。 虽然求解线性方程很容易，但它们的复杂度商有限，因此从数据中学习复杂函数映射的能力较小。 因此，如果没有 AF，神经网络将是一个能力有限的线性回归模型。

这当然不是我们想要的神经网络。 神经网络的任务是计算高度复杂的计算。 此外，没有 AF，神经网络无法学习和建模其他复杂数据，包括图像、语音、视频、音频等。

AF 帮助神经网络理解具有复杂架构的复杂、高维和非线性的大数据集——它们在输入和输出层之间包含多个隐藏层。

阅读：深度学习与神经网络

现在，事不宜迟，让我们深入了解 ANN 中使用的不同类型的激活函数。

激活函数的类型

1. Sigmoid 函数

在 ANN 中，sigmoid 函数是一种非线性 AF，主要用于前馈神经网络。 它是一个可微的实函数，为实输入值定义，并且在任何地方都包含具有特定平滑度的正导数。 sigmoid 函数出现在深度学习模型的输出层，用于预测基于概率的输出。 sigmoid 函数表示为：

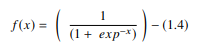
资源

通常，sigmoid 函数的导数被应用于学习算法。 sigmoid 函数的图形是“S”形的。

sigmoid 函数的一些主要缺点包括梯度饱和、收敛缓慢、从更深的隐藏层到输入层的反向传播过程中的陡峭阻尼梯度，以及导致梯度更新在不同方向上传播的非零中心输出。

2.双曲正切函数（Tanh）

双曲正切函数，又名 tanh 函数，是另一种类型的 AF。 它是一个更平滑、以零为中心的函数，范围在 -1 到 1 之间。因此，tanh 函数的输出表示为：

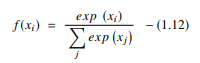
资源

tanh 函数比 sigmoid 函数使用更广泛，因为它为多层神经网络提供了更好的训练性能。 tanh 函数的最大优点是它产生一个以零为中心的输出，从而支持反向传播过程。 tanh 函数主要用于自然语言处理和语音识别任务的循环神经网络。

但是，tanh 函数也有一个局限性——就像 sigmoid 函数一样，它不能解决梯度消失问题。 此外，当输入值为 0（x 为零）时，tanh 函数只能获得 1 的梯度。 结果，该函数在计算过程中会产生一些死神经元。

3.Softmax函数

softmax 函数是另一种用于神经网络的 AF，用于从实数向量计算概率分布。 该函数生成一个介于 0 和 1 之间且概率之和等于 1 的输出。softmax 函数表示如下：

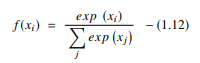
资源

该函数主要用于多类模型，它返回每个类的概率，目标类的概率最高。 它出现在几乎所有使用它们的 DL 架构的输出层中。 sigmoid 和 softmax AF 的主要区别在于前者用于二元分类，后者用于多变量分类。

4.软签功能

softsign 函数是另一种用于神经网络计算的 AF。 虽然它主要用于回归计算问题，但现在它也用于基于 DL 的文本到语音应用程序。 它是一个二次多项式，表示为：

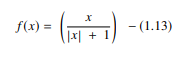
资源

这里“x”等于输入的绝对值。

softsign 函数和 tanh 函数的主要区别在于，与 tanh 函数以指数方式收敛不同，softsign 函数以多项式形式收敛。

5. 整流线性单元（ReLU）函数

DL 模型中最受欢迎的 AF 之一是整流线性单元 (ReLU) 函数，它是一种快速学习的 AF，有望提供最先进的性能和出色的结果。 与 sigmoid 和 tanh 函数等其他 AF 相比，ReLU 函数在深度学习中提供了更好的性能和泛化能力。 该函数是一个近乎线性的函数，保留了线性模型的特性，这使得它们易于使用梯度下降方法进行优化。

ReLU 函数对每个输入元素执行阈值操作，其中所有小于零的值都设置为零。 因此，ReLU 表示为：

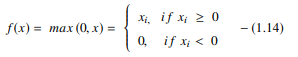
资源

通过纠正小于零的输入值并将其设置为零，该函数消除了在早期类型的激活函数（sigmoid 和 tanh）中观察到的梯度消失问题。

在计算中使用 ReLU 函数最显着的优势是它保证了更快的计算——它不计算指数和除法，从而提高了整体计算速度。 ReLU 函数的另一个关键方面是它通过压缩零到最大值之间的值来在隐藏单元中引入稀疏性。

6. 指数线性单元 (ELU) 函数

指数线性单元 (ELU) 函数是一种 AF，也用于加速神经网络的训练（就像 ReLU 函数一样）。 ELU 函数的最大优点是它可以通过对正值使用恒等以及通过改进模型的学习特性来消除梯度消失问题。

ELU 具有将平均单元激活推向零的负值，从而降低计算复杂度并提高学习速度。 ELU 是 ReLU 的绝佳替代品——它通过在训练过程中将平均激活推向零来减少偏差。

指数线性单位函数表示为：

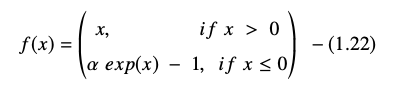
ELU 方程的导数或梯度表示为：

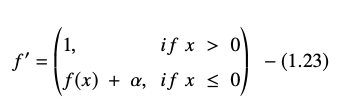
资源

这里“α”等于控制负网络输入饱和点的 ELU 超参数，通常设置为 1.0。 但是，ELU 函数有一个限制——它不是以零为中心的。

结论

如今，像 ReLU 和 ELU 这样的 AF 已经获得了最大的关注，因为它们有助于消除梯度消失问题，该问题会在训练过程中造成重大问题，并降低神经网络模型的准确性和性能。

查看 IIT Madras 的机器学习和云高级认证计划，这是该国最好的工程学校，创建一个计划，不仅可以教您机器学习，还可以使用云基础设施进行有效部署。 我们通过该计划的目标是打开该国最具选择性的学院的大门，并让学习者获得惊人的师资和资源，以掌握高增长的技能