6 rodzajów funkcji aktywacji w sieciach neuronowych, które musisz znać

Ponieważ uczenie głębokie stało się technologią głównego nurtu, ostatnio dużo mówi się o SSN lub sztucznych sieciach neuronowych. Obecnie ANN jest podstawowym elementem w różnych rozwijających się dziedzinach, takich jak rozpoznawanie pisma ręcznego, kompresja obrazów, prognozy giełdowe i wiele innych. Przeczytaj więcej o rodzajach sztucznych sieci neuronowych w uczeniu maszynowym.

Ale czym jest sztuczna sieć neuronowa?

Sztuczna sieć neuronowa to model głębokiego uczenia się, który czerpie inspirację ze struktury neuronowej ludzkiego mózgu. SSN zostały zaprojektowane tak, aby naśladować funkcje ludzkiego mózgu, które uczą się na doświadczeniach i dostosowują do sytuacji. Podobnie jak ludzki mózg ma wielopoziomową strukturę zawierającą miliardy neuronów ułożonych w hierarchię, tak SSN ma również sieć neuronów, które są połączone ze sobą za pomocą aksonów.

Te połączone ze sobą neurony przekazują sygnały elektryczne (zwane synapsami) z jednej warstwy do drugiej. Ta imitacja modelowania mózgu pozwala SSN uczyć się na doświadczeniach bez konieczności interwencji człowieka.

Przeczytaj: Sztuczna sieć neuronowa w eksploracji danych

W ten sposób SSN to złożone struktury zawierające połączone ze sobą elementy adaptacyjne znane jako sztuczne neurony, które mogą wykonywać duże obliczenia w celu reprezentacji wiedzy. Posiadają wszystkie podstawowe cechy biologicznego układu neuronowego, w tym zdolność uczenia się, odporność, nieliniowość, wysoką równoległość, odporność na błędy i uszkodzenia, zdolność do radzenia sobie z nieprecyzyjnymi i rozmytymi informacjami oraz zdolność do uogólniania.

Dołącz do internetowych kursów sztucznej inteligencji z najlepszych światowych uniwersytetów — studiów magisterskich, programów podyplomowych dla kadry kierowniczej oraz zaawansowanego programu certyfikacji w zakresie uczenia maszynowego i sztucznej inteligencji, aby przyspieszyć swoją karierę.

Podstawowe cechy sztucznych sieci neuronowych

• Nieliniowość zapewnia lepsze dopasowanie do danych.
• Wysoka równoległość promuje szybkie przetwarzanie i odporność na awarie sprzętu.
• Generalizacja pozwala na zastosowanie modelu do danych nieuczonych.
• Niewrażliwość na hałas, która umożliwia dokładne przewidywanie nawet w przypadku niepewnych danych i błędów pomiarowych.
• Uczenie się i adaptacyjność pozwalają modelowi aktualizować swoją wewnętrzną architekturę zgodnie ze zmieniającym się środowiskiem.

Obliczenia oparte na SSN mają na celu przede wszystkim zaprojektowanie zaawansowanych algorytmów matematycznych, które umożliwią sztucznym sieciom neuronowym naukę poprzez naśladowanie funkcji przetwarzania informacji i pozyskiwania wiedzy w ludzkim mózgu.

Komponenty sztucznych sieci neuronowych

Sieci SSN składają się z trzech warstw lub faz rdzenia – warstwy wejściowej, warstwy ukrytej/warstw ukrytych i warstwy wyjściowej.

• Warstwa wejściowa: Pierwsza warstwa jest zasilana danymi wejściowymi, czyli surowymi danymi. Przekazuje informacje ze świata zewnętrznego do sieci. W tej warstwie nie są wykonywane żadne obliczenia – węzły jedynie przekazują informacje do warstwy ukrytej.
• Ukryta warstwa: W tej warstwie węzły leżą ukryte za warstwą wejściową – stanowią część abstrakcji w każdej sieci neuronowej. Wszystkie obliczenia dotyczące obiektów wprowadzonych przez warstwę wejściową odbywają się w warstwie ukrytej, a następnie przenosi wynik do warstwy wyjściowej.
• Warstwa wyjściowa: Ta warstwa przedstawia wyniki obliczeń przeprowadzonych przez sieć w świecie zewnętrznym.

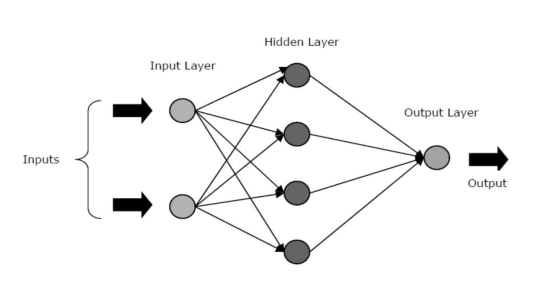
Źródło

Sieci neuronowe można podzielić na różne typy na podstawie aktywności ukrytych warstw. Na przykład w prostej sieci neuronowej jednostki ukryte mogą skonstruować swoją unikalną reprezentację sygnału wejściowego. W tym przypadku wagi pomiędzy jednostkami ukrytymi i wejściowymi decydują o tym, kiedy każda jednostka ukryta jest aktywna.

W ten sposób, dostosowując te wagi, ukryta warstwa może wybrać, co powinna reprezentować. Inne architektury obejmują modele jednowarstwowe i wielowarstwowe. W pojedynczej warstwie jest zwykle tylko warstwa wejściowa i wyjściowa – brakuje w niej warstwy ukrytej. Natomiast w modelu wielowarstwowym istnieje jedna lub więcej niż jedna warstwa ukryta.

Co to są funkcje aktywacji w sieci neuronowej?

Jak wspomnieliśmy wcześniej, SSN są kluczowym elementem wielu struktur, które pomagają zrewolucjonizować otaczający nas świat. Ale czy kiedykolwiek zastanawiałeś się, w jaki sposób SSN zapewniają najnowocześniejszą wydajność, aby znaleźć rozwiązania rzeczywistych problemów?

Odpowiedź brzmi – Funkcje aktywacji.

Sieci SSN wykorzystują funkcje aktywacji (AF) do wykonywania złożonych obliczeń w warstwach ukrytych, a następnie przekazują wynik do warstwy wyjściowej. Podstawowym celem AF jest wprowadzenie nieliniowych właściwości w sieci neuronowej.

Konwertują liniowe sygnały wejściowe węzła na nieliniowe sygnały wyjściowe, aby ułatwić uczenie się wielomianów wyższego rzędu, które przekraczają jeden stopień w przypadku głębokich sieci. Unikalnym aspektem AF jest to, że można je różnicować – to pomaga im funkcjonować podczas wstecznej propagacji sieci neuronowych.

Jaka jest potrzeba nieliniowości?

Jeśli funkcje aktywacji nie zostaną zastosowane, sygnał wyjściowy będzie funkcją liniową, która jest wielomianem jednego stopnia. Chociaż rozwiązywanie równań liniowych jest łatwe, mają one ograniczony iloraz złożoności, a zatem mają mniejszą moc uczenia się złożonych mapowań funkcjonalnych na podstawie danych. Zatem bez AF sieć neuronowa byłaby modelem regresji liniowej o ograniczonych możliwościach.

Z pewnością nie tego chcemy od sieci neuronowej. Zadaniem sieci neuronowych jest wykonywanie bardzo skomplikowanych obliczeń. Ponadto bez AF sieci neuronowe nie mogą uczyć się i modelować innych skomplikowanych danych, w tym obrazów, mowy, filmów, dźwięku itp.

AF pomagają sieciom neuronowym zrozumieć skomplikowane, wielowymiarowe i nieliniowe zbiory Big Data, które mają skomplikowaną architekturę – zawierają wiele ukrytych warstw pomiędzy warstwą wejściową i wyjściową.

Przeczytaj: Głębokie uczenie a sieć neuronowa

Teraz bez dalszych ceregieli przyjrzyjmy się różnym typom funkcji aktywacji używanych w sieciach SSN.

Rodzaje funkcji aktywacji

1. Funkcja sigmoidalna

W SSN funkcja sigmoidalna jest nieliniowym AF stosowanym głównie w sieciach neuronowych ze sprzężeniem do przodu. Jest to różniczkowalna funkcja rzeczywista, zdefiniowana dla rzeczywistych wartości wejściowych i zawierająca wszędzie dodatnie pochodne o określonym stopniu gładkości. Funkcja sigmoidalna pojawia się w warstwie wyjściowej modeli uczenia głębokiego i jest używana do przewidywania wyników opartych na prawdopodobieństwie. Funkcja sigmoidalna jest reprezentowana jako:

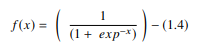
Źródło

Ogólnie pochodne funkcji sigmoidalnej stosuje się do algorytmów uczenia. Wykres funkcji sigmoidalnej ma kształt litery „S”.

Niektóre z głównych wad funkcji sigmoidalnej obejmują nasycenie gradientu, powolną zbieżność, ostre gradienty tłumienia podczas wstecznej propagacji od głębszych warstw ukrytych do warstw wejściowych oraz niezerowe wyśrodkowane wyjście, które powoduje propagację aktualizacji gradientu w różnych kierunkach.

2. Hiperboliczna funkcja styczna (Tanh)

Innym rodzajem AF jest funkcja styczna hiperboliczna, czyli funkcja tanh. Jest to gładsza, wyśrodkowana na zero funkcja mająca zakres od -1 do 1. W rezultacie wynik funkcji tanh jest reprezentowany przez:

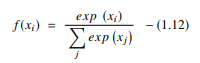
Źródło

Funkcja tanh jest znacznie szerzej wykorzystywana niż funkcja sigmoidalna, ponieważ zapewnia lepszą wydajność uczenia wielowarstwowych sieci neuronowych. Największą zaletą funkcji tanh jest to, że generuje ona wyjście wyśrodkowane na zero, wspierając w ten sposób proces propagacji wstecznej. Funkcja tanh była najczęściej używana w rekurencyjnych sieciach neuronowych do przetwarzania języka naturalnego i zadań rozpoznawania mowy.

Jednak funkcja tanh również ma swoje ograniczenia – podobnie jak funkcja sigmoidalna, nie może rozwiązać problemu znikającego gradientu. Ponadto funkcja tanh może osiągnąć gradient 1 tylko wtedy, gdy wartość wejściowa wynosi 0 (x to zero). W rezultacie funkcja może wytworzyć martwe neurony podczas procesu obliczeniowego.

3. Funkcja Softmax

Funkcja softmax to kolejny typ AF używany w sieciach neuronowych do obliczania rozkładu prawdopodobieństwa z wektora liczb rzeczywistych. Ta funkcja generuje dane wyjściowe, które mieszczą się w zakresie od 0 do 1, a suma prawdopodobieństw jest równa 1. Funkcja softmax jest reprezentowana w następujący sposób:

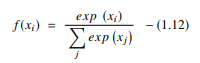
Źródło

Ta funkcja jest używana głównie w modelach wieloklasowych, w których zwraca prawdopodobieństwa każdej klasy, przy czym klasa docelowa ma największe prawdopodobieństwo. Występuje w prawie wszystkich warstwach wyjściowych architektury DL, w których są używane. Podstawowa różnica między AF sigmoidalnym i softmax polega na tym, że podczas gdy pierwszy jest używany w klasyfikacji binarnej, drugi jest używany do klasyfikacji wielowymiarowej.

4. Funkcja Softsign

Funkcja softsign to kolejny AF używany w sieciach neuronowych. Chociaż jest to głównie w problemach z obliczeniami regresji, obecnie jest również używany w aplikacjach DL opartych na zamianie tekstu na mowę. Jest to wielomian kwadratowy, reprezentowany przez:

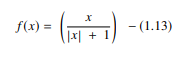
Źródło

Tutaj „x” równa się wartości bezwzględnej wejścia.

Główna różnica między funkcją softsign a funkcją tanh polega na tym, że w przeciwieństwie do funkcji tanh, która zbiega się wykładniczo, funkcja softsign zbiega się w postaci wielomianu.

5. Funkcja rektyfikowanej jednostki liniowej (ReLU)

Jeden z najpopularniejszych AF w modelach DL, funkcja rektyfikowanej jednostki liniowej (ReLU), to szybko uczący się AF, który obiecuje zapewnić najwyższą wydajność i znakomite rezultaty. W porównaniu do innych AF, takich jak funkcje sigmoidalne i tanh, funkcja ReLU oferuje znacznie lepszą wydajność i uogólnienie w głębokim uczeniu. Funkcja jest funkcją prawie liniową, która zachowuje właściwości modeli liniowych, co ułatwia ich optymalizację metodami gradient-descent.

Funkcja ReLU wykonuje operację progową na każdym elemencie wejściowym, gdzie wszystkie wartości mniejsze od zera są ustawione na zero. W związku z tym ReLU jest reprezentowane jako:

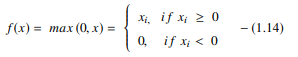
Źródło

Poprzez skorygowanie wartości wejść mniejszych od zera i ustawienie ich na zero, funkcja ta eliminuje problem zanikającego gradientu obserwowany we wcześniejszych typach funkcji aktywacji (sigmoid i tanh).

Najważniejszą zaletą korzystania z funkcji ReLU w obliczeniach jest to, że gwarantuje ona szybsze obliczenia – nie oblicza wykładników i dzieleń, zwiększając w ten sposób ogólną szybkość obliczeń. Innym krytycznym aspektem funkcji ReLU jest to, że wprowadza ona rzadkość w ukrytych jednostkach, zgniatając wartości od zera do maksimum.

6. Funkcja wykładniczych jednostek liniowych (ELU)

Funkcja wykładniczych jednostek liniowych (ELU) to AF, który jest również używany do przyspieszenia uczenia sieci neuronowych (podobnie jak funkcja ReLU). Największą zaletą funkcji ELU jest to, że może ona wyeliminować problem znikającego gradientu, używając tożsamości dla wartości dodatnich i poprawiając charakterystykę uczenia modelu.

Jednostki ELU mają wartości ujemne, które zbliżają średnią aktywację jednostki do zera, zmniejszając w ten sposób złożoność obliczeniową i poprawiając szybkość uczenia się. ELU jest doskonałą alternatywą dla ReLU – zmniejsza przesunięcia obciążenia, przesuwając średnią aktywację do zera podczas procesu treningu.

Wykładnicza funkcja jednostki liniowej jest reprezentowana jako:

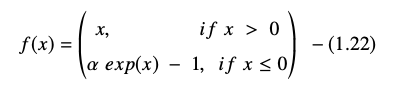
Pochodną lub gradient równania ELU przedstawiono jako:

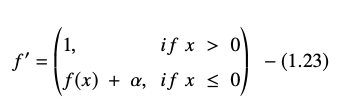
Źródło

Tutaj „α” równa się hiperparametrowi ELU, który kontroluje punkt nasycenia dla ujemnych wejść netto, który zwykle jest ustawiony na 1,0. Funkcja ELU ma jednak pewne ograniczenie – nie jest wyśrodkowana na zero.

Wniosek

Obecnie AF, takie jak ReLU i ELU, zyskały maksymalną uwagę, ponieważ pomagają wyeliminować problem zanikającego gradientu, który powoduje poważne problemy w pociągu procesu uczenia i obniża dokładność i wydajność modeli sieci neuronowych.

Sprawdź Advanced Certification Program in Machine Learning & Cloud z IIT Madras, najlepszą szkołą inżynierską w kraju, aby stworzyć program, który nauczy Cię nie tylko uczenia maszynowego, ale także skutecznego wdrażania go z wykorzystaniem infrastruktury chmury. Naszym celem w ramach tego programu jest otwarcie drzwi najbardziej selektywnego instytutu w kraju i zapewnienie uczniom dostępu do niesamowitych wydziałów i zasobów, aby opanować umiejętność, która jest na wysokim poziomie i rośnie