6 Arten von Aktivierungsfunktionen in neuronalen Netzen, die Sie kennen müssen

Da Deep Learning zu einer Mainstream-Technologie geworden ist, wurde in letzter Zeit viel über ANNs oder künstliche neuronale Netze gesprochen. Heute ist ANN eine Kernkomponente in verschiedenen aufstrebenden Bereichen wie Handschrifterkennung, Bildkomprimierung, Börsenvorhersage und vielem mehr. Lesen Sie mehr über Arten von künstlichen neuronalen Netzen beim maschinellen Lernen.

Aber was ist ein künstliches neuronales Netz?

Artificial Neural Network ist ein Deep-Learning-Modell, das sich von der neuronalen Struktur des menschlichen Gehirns inspirieren lässt. KNNs wurden entwickelt, um die Funktionen des menschlichen Gehirns nachzuahmen, das aus Erfahrungen lernt und sich entsprechend an die Situation anpasst. So wie das menschliche Gehirn eine vielschichtige Struktur mit Milliarden hierarchisch angeordneter Neuronen hat, verfügt auch ANN über ein Netzwerk von Neuronen, die über Axone miteinander verbunden sind.

Diese miteinander verbundenen Neuronen leiten elektrische Signale (sogenannte Synapsen) von einer Schicht zur anderen weiter. Diese Nachahmung der Gehirnmodellierung ermöglicht es dem KNN, aus Erfahrungen zu lernen, ohne dass ein menschliches Eingreifen erforderlich ist.

Lesen Sie: Künstliches neuronales Netzwerk im Data Mining

Somit sind ANNs komplexe Strukturen, die miteinander verbundene adaptive Elemente enthalten, die als künstliche Neuronen bekannt sind und große Berechnungen zur Wissensdarstellung durchführen können. Sie besitzen alle grundlegenden Qualitäten des biologischen Neuronensystems, darunter Lernfähigkeit, Robustheit, Nichtlinearität, hohe Parallelität, Fehler- und Ausfalltoleranz, die Fähigkeit, mit ungenauen und unscharfen Informationen umzugehen, und die Fähigkeit zur Verallgemeinerung.

Nehmen Sie online an den Kursen für künstliche Intelligenz von den besten Universitäten der Welt teil – Master, Executive Post Graduate Programs und Advanced Certificate Program in ML & AI, um Ihre Karriere zu beschleunigen.

Kerneigenschaften künstlicher neuronaler Netze

• Nichtlinearität verleiht den Daten eine bessere Anpassung.
• Hohe Parallelität fördert eine schnelle Verarbeitung und Hardwarefehlertoleranz.
• Die Verallgemeinerung ermöglicht die Anwendung des Modells auf ungelernte Daten.
• Rauschunempfindlichkeit, die eine genaue Vorhersage auch bei unsicheren Daten und Messfehlern ermöglicht.
• Lernen und Adaptivität ermöglichen es dem Modell, seine interne Architektur entsprechend der sich ändernden Umgebung zu aktualisieren.

ANN-basiertes Computing zielt in erster Linie darauf ab, fortschrittliche mathematische Algorithmen zu entwerfen, die es künstlichen neuronalen Netzen ermöglichen, zu lernen, indem sie die Informationsverarbeitungs- und Wissenserwerbsfunktionen des menschlichen Gehirns nachahmen.

Komponenten künstlicher neuronaler Netze

KNNs bestehen aus drei Kernschichten oder -phasen – einer Eingabeschicht, verborgenen Schicht(en) und einer Ausgabeschicht.

• Input Layer: Der erste Layer wird mit dem Input, also Rohdaten, gespeist. Es übermittelt die Informationen von der Außenwelt an das Netzwerk. In dieser Schicht wird keine Berechnung durchgeführt – die Knoten geben die Informationen lediglich an die verborgene Schicht weiter.
• Hidden Layer: In dieser Schicht liegen die Knoten hinter der Eingabeschicht verborgen – sie bilden den Abstraktionsteil in jedem neuronalen Netz. Alle Berechnungen für die über die Eingabeschicht eingegebenen Features erfolgen in der/den verborgenen Schicht/en und übertragen das Ergebnis dann an die Ausgabeschicht.
• Ausgabeschicht: Diese Schicht bildet die Ergebnisse der vom Netzwerk durchgeführten Berechnungen nach außen ab.

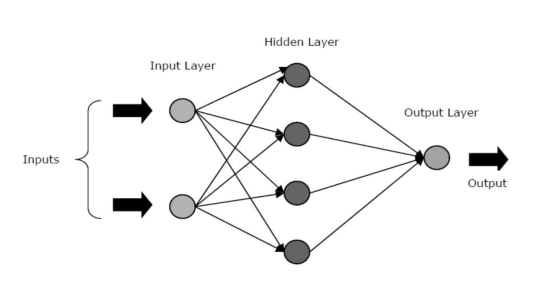
Quelle

Neuronale Netze können basierend auf der Aktivität der verborgenen Schicht(en) in verschiedene Typen eingeteilt werden. Beispielsweise können in einem einfachen neuronalen Netzwerk die verborgenen Einheiten ihre einzigartige Darstellung der Eingabe konstruieren. Hier entscheiden die Gewichtungen zwischen den verborgenen und den eingegebenen Einheiten, wann jede verborgene Einheit aktiv ist.

Somit kann die verborgene Schicht durch Anpassen dieser Gewichtungen auswählen, was sie darstellen soll. Andere Architekturen umfassen die Einzelschicht- und Mehrschichtmodelle. In einer einzelnen Schicht gibt es normalerweise nur eine Eingabe- und Ausgabeschicht – es fehlt eine verborgene Schicht. Dagegen gibt es in einem mehrschichtigen Modell eine oder mehr als eine verborgene Schicht.

Was sind Aktivierungsfunktionen in einem neuronalen Netzwerk?

Wie wir bereits erwähnt haben, sind ANNs eine entscheidende Komponente vieler Strukturen, die dazu beitragen, die Welt um uns herum zu revolutionieren. Aber haben Sie sich jemals gefragt, wie KNNs eine hochmoderne Leistung liefern, um Lösungen für reale Probleme zu finden?

Die Antwort lautet – Aktivierungsfunktionen.

KNNs verwenden Aktivierungsfunktionen (AFs), um komplexe Berechnungen in den verborgenen Schichten durchzuführen und das Ergebnis dann an die Ausgabeschicht zu übertragen. Der Hauptzweck von AFs besteht darin, nichtlineare Eigenschaften in das neuronale Netzwerk einzuführen.

Sie wandeln die linearen Eingangssignale eines Knotens in nichtlineare Ausgangssignale um, um das Lernen von Polynomen höherer Ordnung zu erleichtern, die für tiefe Netzwerke über ein Grad hinausgehen. Ein einzigartiger Aspekt von AFs ist, dass sie differenzierbar sind – dies hilft ihnen, während der Backpropagation der neuronalen Netze zu funktionieren.

Wozu braucht man Nichtlinearität?

Wenn keine Aktivierungsfunktionen angewendet werden, wäre das Ausgangssignal eine lineare Funktion, die ein Polynom von einem Grad ist. Während es einfach ist, lineare Gleichungen zu lösen, haben sie einen begrenzten Komplexitätsquotienten und daher weniger Möglichkeiten, komplexe funktionale Abbildungen aus Daten zu lernen. Somit wäre ein neuronales Netzwerk ohne AFs ein lineares Regressionsmodell mit begrenzten Fähigkeiten.

Dies ist sicherlich nicht das, was wir von einem neuronalen Netzwerk erwarten. Die Aufgabe neuronaler Netze besteht darin, hochkomplizierte Berechnungen durchzuführen. Darüber hinaus können neuronale Netze ohne AFs keine anderen komplizierten Daten lernen und modellieren, einschließlich Bilder, Sprache, Videos, Audio usw.

AFs helfen neuronalen Netzwerken, komplizierte, hochdimensionale und nichtlineare Big Data-Sets mit einer komplizierten Architektur zu verstehen – sie enthalten mehrere verborgene Schichten zwischen der Eingabe- und Ausgabeschicht.

Lesen Sie: Deep Learning vs. neuronales Netzwerk

Lassen Sie uns nun ohne weiteres in die verschiedenen Arten von Aktivierungsfunktionen eintauchen, die in KNNs verwendet werden.

Arten von Aktivierungsfunktionen

1. Sigmoidfunktion

In einem KNN ist die Sigmoidfunktion eine nichtlineare AF, die hauptsächlich in neuronalen Feedforward-Netzen verwendet wird. Es ist eine differenzierbare reelle Funktion, die für reelle Eingabewerte definiert ist und überall positive Ableitungen mit einem bestimmten Grad an Glättung enthält. Die Sigmoidfunktion erscheint in der Ausgabeschicht der Deep-Learning-Modelle und wird zur Vorhersage wahrscheinlichkeitsbasierter Ausgaben verwendet. Die Sigmoidfunktion wird dargestellt als:

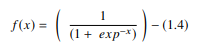
Quelle

Im Allgemeinen werden die Ableitungen der Sigmoidfunktion auf Lernalgorithmen angewendet. Der Graph der Sigmoidfunktion ist 'S'-förmig.

Einige der Hauptnachteile der Sigmoid-Funktion umfassen Gradientensättigung, langsame Konvergenz, scharfe Dämpfungsgradienten während der Rückausbreitung von innerhalb tiefer verborgener Schichten zu den Eingangsschichten und eine von Null verschiedene zentrierte Ausgabe, die bewirkt, dass sich die Gradientenaktualisierungen in unterschiedliche Richtungen ausbreiten.

2. Funktion des hyperbolischen Tangens (Tanh)

Die hyperbolische Tangensfunktion, auch bekannt als Tanh-Funktion, ist eine andere Art von AF. Es ist eine glattere, nullzentrierte Funktion mit einem Bereich zwischen -1 und 1. Als Ergebnis wird die Ausgabe der tanh-Funktion dargestellt durch:

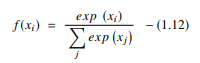
Quelle

Die tanh-Funktion wird viel häufiger verwendet als die Sigmoid-Funktion, da sie eine bessere Trainingsleistung für mehrschichtige neuronale Netze liefert. Der größte Vorteil der tanh-Funktion besteht darin, dass sie eine nullzentrierte Ausgabe erzeugt und dadurch den Backpropagation-Prozess unterstützt. Die tanh-Funktion wurde hauptsächlich in rekurrenten neuronalen Netzwerken für die Verarbeitung natürlicher Sprache und Spracherkennungsaufgaben verwendet.

Allerdings hat auch die Tanh-Funktion eine Einschränkung – ebenso wie die Sigmoid-Funktion kann sie das Problem des verschwindenden Gradienten nicht lösen. Außerdem kann die tanh-Funktion nur dann einen Gradienten von 1 erreichen, wenn der Eingangswert 0 ist (x ist null). Infolgedessen kann die Funktion während des Berechnungsprozesses einige tote Neuronen erzeugen.

3. Softmax-Funktion

Die Softmax-Funktion ist eine andere Art von AF, die in neuronalen Netzwerken verwendet wird, um die Wahrscheinlichkeitsverteilung aus einem Vektor reeller Zahlen zu berechnen. Diese Funktion generiert eine Ausgabe, die zwischen den Werten 0 und 1 liegt und bei der die Summe der Wahrscheinlichkeiten gleich 1 ist. Die Softmax-Funktion wird wie folgt dargestellt:

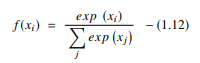
Quelle

Diese Funktion wird hauptsächlich in Mehrklassenmodellen verwendet, wo sie Wahrscheinlichkeiten jeder Klasse zurückgibt, wobei die Zielklasse die höchste Wahrscheinlichkeit hat. Es erscheint in fast allen Ausgabeschichten der DL-Architektur, wo sie verwendet werden. Der Hauptunterschied zwischen dem Sigmoid- und dem Softmax-AF besteht darin, dass ersteres für die binäre Klassifikation, letzteres für die multivariate Klassifikation verwendet wird.

4. Softsign-Funktion

Die Softsign-Funktion ist eine weitere AF, die beim Rechnen mit neuronalen Netzwerken verwendet wird. Obwohl es sich hauptsächlich um Regressionsberechnungsprobleme handelt, wird es heutzutage auch in DL-basierten Text-zu-Sprache-Anwendungen verwendet. Es ist ein quadratisches Polynom, dargestellt durch:

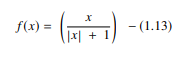
Quelle

Hier ist „x“ gleich dem absoluten Wert der Eingabe.

Der Hauptunterschied zwischen der Softsign-Funktion und der tanh-Funktion besteht darin, dass im Gegensatz zur tanh-Funktion, die exponentiell konvergiert, die Softsign-Funktion in Polynomform konvergiert.

5. Funktion der gleichgerichteten linearen Einheit (ReLU).

Einer der beliebtesten AFs in DL-Modellen, die Rectified Linear Unit (ReLU)-Funktion, ist ein schnell lernender AF, der hochmoderne Leistung mit hervorragenden Ergebnissen verspricht. Im Vergleich zu anderen AFs wie den Sigmoid- und Tanh-Funktionen bietet die ReLU-Funktion eine viel bessere Leistung und Generalisierung beim Deep Learning. Die Funktion ist eine nahezu lineare Funktion, die die Eigenschaften linearer Modelle beibehält, wodurch sie mit Gradientenabstiegsmethoden einfach zu optimieren sind.

Die ReLU-Funktion führt an jedem Eingabeelement eine Schwellenoperation durch, bei der alle Werte kleiner als null auf null gesetzt werden. Somit wird die ReLU dargestellt als:

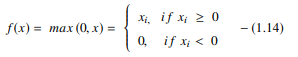
Quelle

Indem die Werte der Eingaben kleiner als null korrigiert und auf null gesetzt werden, beseitigt diese Funktion das Problem des verschwindenden Gradienten, das bei den früheren Arten von Aktivierungsfunktionen (Sigmoid und Tanh) beobachtet wurde.

Der bedeutendste Vorteil der Verwendung der ReLU-Funktion bei der Berechnung besteht darin, dass sie eine schnellere Berechnung garantiert – sie berechnet keine Exponentiale und Divisionen, wodurch die Gesamtberechnungsgeschwindigkeit erhöht wird. Ein weiterer kritischer Aspekt der ReLU-Funktion besteht darin, dass sie Sparsity in die verborgenen Einheiten einführt, indem sie die Werte zwischen null und maximal quetscht.

6. Funktion der exponentiellen linearen Einheiten (ELUs).

Die Funktion der exponentiellen linearen Einheiten (ELUs) ist eine AF, die auch verwendet wird, um das Training neuronaler Netze zu beschleunigen (genau wie die ReLU-Funktion). Der größte Vorteil der ELU-Funktion besteht darin, dass sie das Problem des verschwindenden Gradienten eliminieren kann, indem sie Identität für positive Werte verwendet und die Lerneigenschaften des Modells verbessert.

ELUs haben negative Werte, die die mittlere Einheitenaktivierung näher an Null bringen, wodurch die Rechenkomplexität verringert und die Lerngeschwindigkeit verbessert wird. Die ELU ist eine hervorragende Alternative zur ReLU – sie verringert Verzerrungsverschiebungen, indem sie die mittlere Aktivierung während des Trainingsprozesses gegen Null drückt.

Die exponentielle lineare Einheitsfunktion wird dargestellt als:

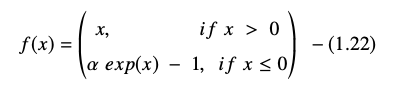
Die Ableitung oder Steigung der ELU-Gleichung wird dargestellt als:

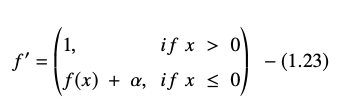
Quelle

Hier entspricht „α“ dem ELU-Hyperparameter, der den Sättigungspunkt für negative Nettoeingaben steuert, der normalerweise auf 1,0 eingestellt ist. Die ELU-Funktion hat jedoch eine Einschränkung – sie ist nicht nullzentriert.

Fazit

Heutzutage haben AFs wie ReLU und ELU maximale Aufmerksamkeit erlangt, da sie dazu beitragen, das Problem des verschwindenden Gradienten zu beseitigen, das große Probleme im Trainingsprozess verursacht und die Genauigkeit und Leistung von neuronalen Netzwerkmodellen verschlechtert.

Informieren Sie sich über das Advanced Certification Program in Machine Learning & Cloud mit IIT Madras, der besten Ingenieurschule des Landes, um ein Programm zu erstellen, das Ihnen nicht nur maschinelles Lernen beibringt, sondern auch den effektiven Einsatz davon mithilfe der Cloud-Infrastruktur. Unser Ziel mit diesem Programm ist es, die Türen des selektivsten Instituts des Landes zu öffnen und den Lernenden Zugang zu erstaunlichen Fakultäten und Ressourcen zu verschaffen, um eine Fähigkeit zu meistern, die hoch ist und wächst