Bausteine ​​neuronaler Netze: Komponenten neuronaler Netze erklärt

Einführung

In den letzten Jahren hat die Popularität von Deep Learning in Bezug auf Nutzung und Anwendung in allen Bereichen der Industrie einen abrupten Anstieg genommen. Ob Bilderkennung, Spracherzeugung, Übersetzung und viele weitere Anwendungen dieser Art, fast jedes Unternehmen möchte diese Technologie in das eine oder andere Produkt integrieren, das es entwickelt. Der Grund für diese Überlegenheit gegenüber herkömmlichen maschinellen Lernalgorithmen ist die Genauigkeit und effiziente Leistung, die diese Deep-Learning-Modelle bieten.

Obwohl die Infrastruktur eine wichtige Rolle bei der Bereitstellung dieser Ergebnisse spielt, übernimmt der Kerncode die gesamte Verarbeitung, die in einem neuronalen Netzwerk eingeschlossen ist. Lassen Sie uns die verschiedenen Komponenten dieses Netzwerks untersuchen und dann einige grundlegende Einheiten betrachten, die diese Komponenten verwenden.

Muss gelesen werden: Einführung in das neuronale Netzwerkmodell

Verschiedene Komponenten des neuronalen Netzwerks

Neuron

Der Grundbaustein eines neuronalen Netzes ist ein Neuron. Dieses Konzept ist dem eigentlichen neuronalen Netzwerk in unserem menschlichen Gehirn sehr ähnlich. Dieses künstliche Neuron nimmt alle Eingaben, aggregiert sie und gibt dann basierend auf einer Funktion die Ausgabe des Neurons aus.

Ein neuronales Netzwerk umfasst viele solcher Neuronen, die in Form von Schichten, die als Eingangs-, verborgene und Ausgangsschichten bekannt sind, miteinander verbunden sind. Dieses Netzwerk ermöglicht es uns, beliebige komplexe Datenmuster auf eine mathematische Funktion abzubilden, was mathematisch mit dem universellen Approximationssatz verifiziert werden kann.

Gewichte

Das Modell kann Gewichte haben, um hohe Werte mit negativen Werten zu unterdrücken. Sie können dies am Beispiel eines Smartphone-Kaufs interpretieren. Je höher der Preis, desto geringer sind die Chancen, dieses Smartphone zu kaufen, aber wenn unser Modell alle Werte addiert und mit dem Schwellenwert vergleicht, kann die falsche Vorhersage getroffen werden. Um diesen Effekt aufzuheben, sollten negative Gewichtungen die Summe reduzieren und die richtige Vorhersage erhalten.

Aktivierungsfunktion

In der Neuronendefinition wurde erwähnt, dass das Neuron das Ergebnis basierend auf einer Funktion entweder an die nächste Schicht ausgibt, wenn es Teil der Eingabe- oder verborgenen Schicht ist, oder für die weitere Verarbeitung in der Ausgabeschicht verwendet wird.

Diese Funktion wird als Aktivierungsfunktion bezeichnet und definiert den Zustand des Neurons. Es gibt viele Aktivierungsfunktionen auf dem Markt, die diese Aufgabe erfüllen können, aber alles hängt vom Anwendungsfall ab. Beispiele sind die Sigmoid-Funktion, die Tanh-Funktion, die Softmax-Funktion, Relu (rektifizierte lineare Einheit), Leaky Relu und viele mehr.

Lernrate

Es kann das Tempo der Gewichtsaktualisierung steuern. Betrachten Sie zwei Fälle, in denen die Lernrate ein wichtiger Faktor ist. Wenn ein Eingabemerkmal weniger Werte hat, müssen wir die Gewichtungen häufiger aktualisieren, und deshalb ist eine größere Lernrate erwünscht. In ähnlicher Weise kann eine niedrige Lernrate in dichten Daten funktionieren.

Schauen wir uns einige grundlegende Einheiten an, die diese Komponenten in größeren neuronalen Netzen verwenden.

MP-Neuron

Dies ist die grundlegendste Form eines künstlichen Neurons, das die Eingabesumme berechnet und sie dann an die Aktivierungsfunktion weitergibt, um die endgültige Ausgabe zu erhalten. Hier ist ein Bild davon:

Der einschränkende Faktor dabei ist, dass die Eingaben binär sein sollten und keine reelle Zahl erlaubt ist. Das heißt, wenn wir einen Datensatz mit unterschiedlichen Werten verwenden möchten, muss dieser auf Binär skaliert werden, um an das Modell übergeben zu werden.

Die Ausgaben dieses Modells sind ebenfalls binär, was es schwierig macht, die Qualität der Ergebnisse zu interpretieren. Die Eingaben haben keine Gewichtung, daher können wir nicht kontrollieren, wie viel Beitrag eine Funktion zum Ergebnis leisten wird.

Perzeptron-Neuron

Einer der wesentlichen Nachteile von MP-Neuronen war, dass sie keine reellen Zahlen als Eingaben akzeptieren können, was zu unerwünschten Ergebnissen führen kann. Das heißt, wenn wir diesem Neuron ein Eingabemerkmal mit reellen Zahlen übergeben wollen, muss es auf 1 oder 0 herunterskaliert werden. In diesem Neuronenmodell gibt es keine solche Beschränkung der Eingaben, aber das Passieren standardisierter Eingaben wird in kürzerer Zeit zu besseren Ergebnissen führen, da die Aggregation von Eingaben für alle Merkmalswerte fair wäre.

Außerdem wird ein Lernalgorithmus eingeführt, der dieses Modell noch robuster gegenüber neuen Eingaben macht. Der Algorithmus aktualisiert die auf jeden Eingang angewendeten Gewichtungen basierend auf der Verlustfunktion. Die Verlustfunktion bestimmt die Differenz zwischen dem tatsächlichen Wert und dem vom Modell vorhergesagten Wert. Der quadrierte Fehlerverlust ist eine solche beliebte Funktion, die in Deep-Learning-Modellen verwendet wird.

Da das Wahrnehmungsneuron auch eine binäre Ausgabe ausgibt, kann der Verlust null oder eins sein. Das bedeutet, dass wir die Verlustfunktion dieses Typs kompakter definieren können als „Wenn die Vorhersage nicht gleich dem wahren Wert ist, ist der Verlust eins und die Gewichtungen müssen aktualisiert werden, andernfalls kein Verlust und keine Aktualisierung erforderlich“. Die Aktualisierungen in den Gewichtungen erfolgen auf folgende Weise:

w = w + x wenn wx < 0

w = w – x wenn wx >= 0

Lesen Sie: TensorFlow-Objekterkennungs-Tutorial für Anfänger

Sigmaneuron

Das Perzeptron-Neuron scheint im Vergleich zum MP-Neuron vielversprechend zu sein, aber es gibt noch einige Probleme, die angegangen werden müssen. Ein großer Fehler bei beiden ist, dass sie nur die binäre Klassifizierung unterstützen. Ein weiteres Problem sind die harten Klassifizierungsgrenzen, die nur ausgeben, ob ein bestimmter Fall möglich ist. Es erlaubt keine Flexibilität bei Vorhersagen in Form von Wahrscheinlichkeiten, die besser interpretierbar sind als binäre Ausgaben.

Um all diese Probleme zu lösen, wurde das Sigmoid-Neuron eingeführt, das für Mehrfachklassifizierung und Regressionsaufgaben verwendet werden kann. Dieses Modell verwendet die Sigmoid-Familie von Funktionen oder logarithmisch:

y = 1 / (1 + e^ (-wx + b))

Wenn wir diese Funktion grafisch darstellen, würde sie die 'S'-Form annehmen, wo ihre Position angepasst werden kann, indem verschiedene Werte von 'b' verwendet werden, was der Schnittpunkt dieser Kurve ist. Der Ausgang dieser Funktion liegt immer zwischen 0 und 1, egal wie viele Eingänge übergeben werden. Dies gibt die Wahrscheinlichkeit der Klasse aus, was besser ist als starre Ausgaben. Dies bedeutet auch, dass wir mehrere Klassifizierungen haben oder eine Regression durchführen können.

Der Lernalgorithmus dafür unterscheidet sich von den vorherigen. Hier werden die Gewichte und Bias gemäß der Ableitung der Verlustfunktion aktualisiert.

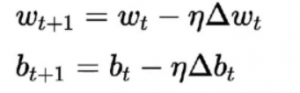
Dieser Algorithmus ist allgemein als Gradientenabstiegsregel bekannt. Die Herleitung und ausführliche Erklärung dafür ist recht langwierig und mathematisch, daher entfällt derzeit dieser Artikel. Einfach ausgedrückt besagt es, dass wir uns in eine dem Gradienten entgegengesetzte Richtung bewegen sollten, um optimale Minima für die Ableitung der Verlustfunktion zu erhalten.

Fazit

Dies war eine kurze Einführung in neuronale Netze. Wir haben die verschiedenen grundlegenden Komponenten gesehen, wie das Neuron, das als Mini-Gehirn fungiert und die Eingaben verarbeitet, Gewichte, die es ermöglichen, Werte auszugleichen, die Lernrate, um zu steuern, wie das Tempo der Gewichte aktualisiert wird, und die Aktivierungsfunktion, um die Neuronen zu aktivieren.

Wir haben auch gesehen, wie der Grundbaustein Neuron bei zunehmender Komplexität der Aufgabe unterschiedliche Formen annehmen kann. Wir begannen mit der grundlegendsten Form im MP-Neuron, beseitigten dann einige Probleme im Perzeptron-Neuron und fügten später Unterstützung für Regressions- und Mehrklassen-Klassifizierungsaufgaben im Sigmoid-Neuron hinzu.

Wenn Sie mehr über maschinelles Lernen erfahren möchten, sehen Sie sich das PG-Diplom in maschinellem Lernen und KI von IIIT-B & upGrad an, das für Berufstätige konzipiert ist und mehr als 450 Stunden strenge Schulungen, mehr als 30 Fallstudien und Aufgaben bietet, IIIT- B-Alumni-Status, mehr als 5 praktische, praktische Abschlussprojekte und Jobunterstützung bei Top-Unternehmen.