Una introducción a la red neuronal Feedforward: capas, funciones e importancia
Publicado: 2020-05-28La tecnología de aprendizaje profundo es la columna vertebral de los motores de búsqueda, la traducción automática y las aplicaciones móviles. Funciona imitando el cerebro humano para encontrar y crear patrones a partir de diferentes tipos de datos.
Una parte importante de esta increíble tecnología es una red neuronal de avance, que ayuda a los ingenieros de software en el reconocimiento y la clasificación de patrones, la regresión no lineal y la aproximación de funciones.
Veamos algunas ideas sobre este aspecto esencial de la arquitectura de la red neuronal central.
Tabla de contenido
¿Qué es la red neuronal Feedforward?
Comúnmente conocidas como una red multicapa de neuronas, las redes neuronales feedforward se denominan así debido al hecho de que toda la información viaja solo en la dirección de avance.
La información ingresa primero a los nodos de entrada, se mueve a través de las capas ocultas y finalmente sale a través de los nodos de salida. La red no contiene conexiones para alimentar la información que sale del nodo de salida de vuelta a la red.
Las redes neuronales feedforward están destinadas a aproximar funciones.

Así es como funciona .
Hay un clasificador y = f*(x).
Esto alimenta la entrada x en la categoría y.
La red feedforward mapeará y = f (x; θ). Luego memoriza el valor de θ que se aproxima mejor a la función.
Red neuronal feedforward como base para el reconocimiento de objetos en imágenes, como puedes ver en la aplicación Google Photos.
Las capas de una red neuronal feedforward
Una red neuronal feedforward consta de lo siguiente.
Capa de entrada
Contiene las neuronas receptoras de entrada. Luego pasan la entrada a la siguiente capa. El número total de neuronas en la capa de entrada es igual a los atributos en el conjunto de datos.
capa oculta
Esta es la capa intermedia, escondida entre las capas de entrada y salida. Hay una gran cantidad de neuronas en esta capa que aplican transformaciones a las entradas. Luego lo pasan a la capa de salida.
Capa de salida
Es la última capa y depende de la construcción del modelo. Además, la capa de salida es la característica predicha, ya que sabe cuál desea que sea el resultado.
Pesos de neuronas
La fuerza de una conexión entre las neuronas se llama pesos. El valor de un peso oscila entre 0 y 1.
Saber más: Modelo de Red Neuronal: Breve Introducción, Glosario
Función de costo en la red neuronal Feedforward
La elección de la función de costo es una de las partes más importantes de una red neuronal feedforward. Por lo general, los pequeños cambios en los pesos y sesgos no afectan los puntos de datos clasificados. Por lo tanto, encontrar una manera de mejorar el rendimiento mediante el uso de una función de costo uniforme para realizar pequeños cambios en los pesos y sesgos.
La fórmula para la función de costo del error cuadrático medio es:
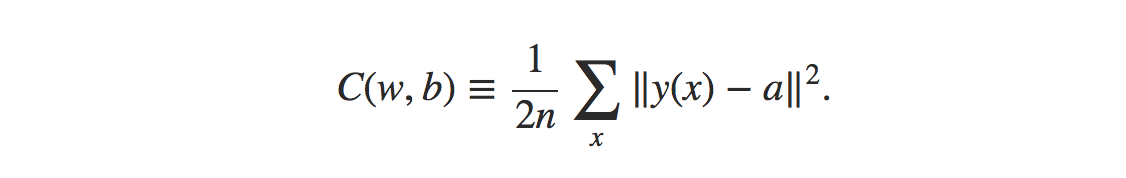
Fuente
Donde,
w = colección de pesos en la red
b = sesgos
n = número de entradas de entrenamiento
a = vectores de salida
x = entrada
‖v‖ = longitud habitual del vector v
Función de pérdida en la red neuronal Feedforward
La función de pérdida en la red neuronal está destinada a determinar si hay alguna corrección que necesita el proceso de aprendizaje.
Las neuronas de la capa de salida serán iguales al número de clases. Comparar la diferencia entre la distribución de probabilidad predicha y la verdadera.
La pérdida de entropía cruzada para la clasificación binaria es:
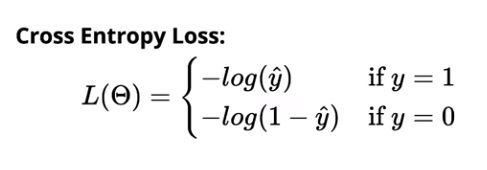
La pérdida de entropía cruzada para la clasificación multiclase es:

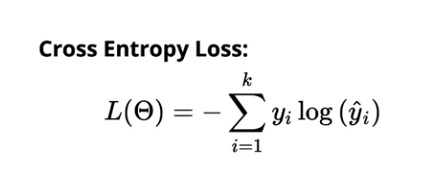
Fuente
Algoritmo de aprendizaje de gradiente
Este algoritmo ayuda a determinar todos los mejores valores posibles de los parámetros para disminuir la pérdida en la red neuronal de avance.

Imagen
Todos los pesos (w₁₁₁, w₁₁₂,...) y sesgos b (b₁, b₂,...) se inicializan aleatoriamente. Una vez hecho esto, se iteran las observaciones en los datos. Luego, la distribución pronosticada correspondiente se determina contra cada observación. Finalmente, la pérdida se calcula utilizando la función de entropía cruzada.
El valor de pérdida luego ayuda a calcular los cambios que se deben realizar en los pesos para disminuir la pérdida general del modelo.
Leer: 13 ideas y temas interesantes sobre proyectos de redes neuronales
La necesidad de un modelo de neurona
Digamos que las entradas que se alimentan a la red son datos de píxeles sin procesar que provienen de una imagen escaneada de un personaje. Para que la salida en la red clasifique el dígito correctamente, querrá determinar la cantidad correcta de pesos y sesgos.
Ahora, necesitaría hacer pequeños cambios en el peso de la red para ver cómo funcionaría el aprendizaje. Para que esto resulte perfecto, pequeños cambios en los pesos solo deberían conducir a pequeños cambios en la salida.
Sin embargo, ¿qué pasa si el pequeño cambio en el peso equivale a un gran cambio en la salida? El modelo de neurona sigmoidea puede resolver este problema.
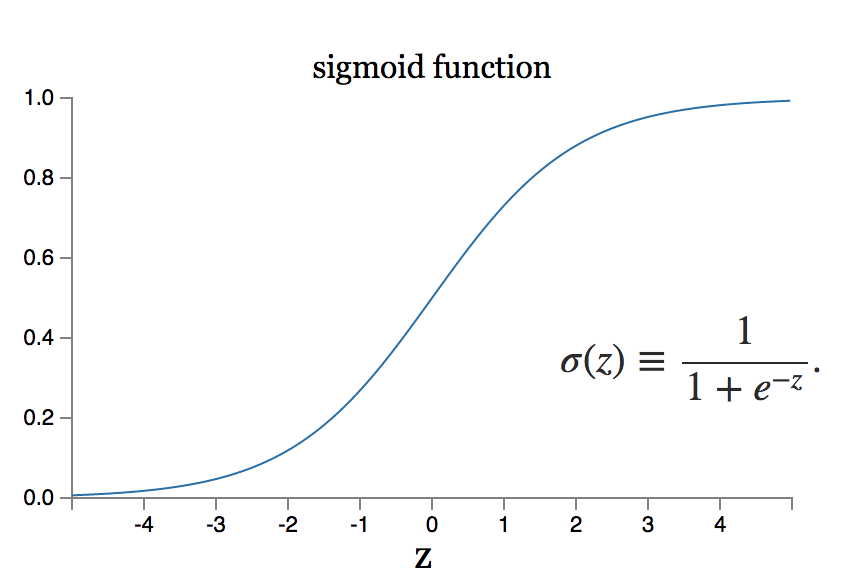
Fuente
Lea también: Los 7 tipos de redes neuronales artificiales que necesitan los ingenieros de ML

Conclusión
El aprendizaje profundo es un territorio de ingeniería de software con un alcance colosal de investigación. Hay muchas arquitecturas de redes neuronales actualizadas para varios tipos de datos. Los sistemas neuronales convolucionales, por ejemplo, han logrado la mejor ejecución de su clase en los campos de los procedimientos de manejo de imágenes, mientras que los sistemas neuronales recurrentes generalmente se utilizan en el procesamiento de contenido y voz.
Cuando se aplican a grandes conjuntos de datos, los sistemas neuronales necesitan medidas monstruosas de potencia computacional y aceleración de equipos, lo que se puede lograr mediante el diseño de unidades de procesamiento de gráficos o GPU. Si es nuevo en el uso de GPU, puede encontrar configuraciones configuradas gratuitas en la web. Los más preferidos son Kaggle Notebooks o Google Collab Notebooks.
Para lograr una red neuronal feedforward eficaz, debe realizar varias iteraciones en la arquitectura de la red, lo que requiere una gran cantidad de pruebas.
Para obtener más información sobre cómo funcionan estas redes, aprenda de los expertos de upGrad. Nuestros cursos son increíblemente completos y puede resolver sus consultas poniéndose en contacto directamente con nuestros profesores experimentados y los mejores de su clase.
Si está interesado en obtener más información sobre el aprendizaje automático, consulte el Diploma PG en aprendizaje automático e IA de IIIT-B y upGrad, que está diseñado para profesionales que trabajan y ofrece más de 450 horas de capacitación rigurosa, más de 30 estudios de casos y asignaciones, IIIT- B Estado de exalumno, más de 5 proyectos prácticos finales prácticos y asistencia laboral con las mejores empresas.
¿Se requiere álgebra lineal en las redes neuronales?
Una red neuronal es un modelo matemático que resuelve cualquier problema complejo. La red toma un conjunto de entradas y calcula un conjunto de salidas con el objetivo de lograr el resultado deseado. Cuando se estudia la teoría de redes neuronales, la mayoría de las neuronas y capas se formatean con frecuencia en álgebra lineal. El álgebra lineal es necesaria para construir el modelo matemático. También puede usar álgebra lineal para comprender la red del modelo. Por lo tanto, para responder a la pregunta, sí, el conocimiento básico de álgebra lineal es obligatorio al usar redes neuronales.
¿Qué se entiende por retropropagación en las redes neuronales?
En el caso de redes neuronales que emplean descenso de gradiente, se utiliza backpropagation. Este algoritmo estima el gradiente de la función de error con respecto a los pesos de la red neuronal y es esencialmente una propagación hacia atrás de errores. Este enfoque se emplea porque el ajuste fino de los pesos reduce las tasas de error y, por lo tanto, mejora la generalización del modelo de red neuronal, haciéndolo más confiable. La retropropagación se clasifica comúnmente como una forma de aprendizaje automático supervisado, ya que requiere un resultado previsto conocido para cada valor de entrada a fin de calcular el gradiente de la función de pérdida en las redes neuronales.
¿En qué se diferencia la retropropagación de los optimizadores?
En las redes neuronales, se utilizan tanto los optimizadores como el algoritmo de retropropagación, y trabajan juntos para hacer que el modelo sea más confiable. La retropropagación se usa para calcular gradientes de manera eficiente, y los optimizadores se usan para entrenar la red neuronal usando los gradientes obtenidos usando la retropropagación. En pocas palabras, lo que hace la retropropagación por nosotros es calcular gradientes, que posteriormente utilizan los optimizadores.
