Wprowadzenie do feedforward sieci neuronowej: warstwy, funkcje i znaczenie

Technologia głębokiego uczenia jest podstawą wyszukiwarek, tłumaczenia maszynowego i aplikacji mobilnych. Działa naśladując ludzki mózg, aby znajdować i tworzyć wzorce z różnych rodzajów danych.

Jedną z ważnych części tej niesamowitej technologii jest sprzężeniowa sieć neuronowa, która pomaga inżynierom oprogramowania w rozpoznawaniu i klasyfikacji wzorców, regresji nieliniowej i aproksymacji funkcji.

Przyjrzyjmy się bliżej temu istotnemu aspektowi architektury rdzeniowej sieci neuronowej.

Co to jest sieć neuronowa Feedforward?

Powszechnie znane jako wielowarstwowa sieć neuronów, sieci neuronowe ze sprzężeniem do przodu są tak nazywane ze względu na fakt, że wszystkie informacje przemieszczają się tylko w kierunku do przodu.

Informacja najpierw wchodzi do węzłów wejściowych, przechodzi przez ukryte warstwy, a na końcu wychodzi przez węzły wyjściowe. Sieć nie zawiera połączeń do przesyłania informacji wychodzących w węźle wyjściowym z powrotem do sieci.

Sieci neuronowe ze sprzężeniem do przodu służą do przybliżania funkcji.

Oto jak to działa .

Istnieje klasyfikator y = f*(x).

Daje to wejście x do kategorii y.

Sieć feedforward odwzoruje y = f (x; θ). Następnie zapamiętuje wartość θ, która najlepiej przybliża funkcję.

Sieć neuronowa typu feedforward dla bazy do rozpoznawania obiektów na obrazach, jak można to zauważyć w aplikacji Zdjęcia Google.

Warstwy feedforward sieci neuronowej

Sieć neuronowa ze sprzężeniem do przodu składa się z następujących elementów.

Warstwa wejściowa

Zawiera neurony odbierające dane wejściowe. Następnie przekazują dane wejściowe do następnej warstwy. Całkowita liczba neuronów w warstwie wejściowej jest równa atrybutom w zbiorze danych.

Ukryta warstwa

Jest to warstwa środkowa, ukryta między warstwą wejściową i wyjściową. W tej warstwie znajduje się ogromna liczba neuronów, które wprowadzają transformacje do wejść. Następnie przekazują go do warstwy wyjściowej.

Warstwa wyjściowa

Jest to ostatnia warstwa i zależy od budowy modelu. Ponadto warstwa wyjściowa jest przewidywaną funkcją, ponieważ wiesz, jaki ma być wynik.

Wagi neuronów

Siła połączenia między neuronami nazywana jest wagami. Wartość wagi waha się od 0 do 1.

Dowiedz się więcej: Model sieci neuronowej: krótkie wprowadzenie, słowniczek

Funkcja kosztów w feedforward sieci neuronowej

Wybór funkcji kosztu jest jedną z najważniejszych części sieci neuronowej ze sprzężeniem do przodu. Zwykle niewielkie zmiany wag i odchyleń nie wpływają na sklasyfikowane punkty danych. Tak więc, aby znaleźć sposób na poprawę wydajności za pomocą funkcji gładkiego kosztu, aby wprowadzić niewielkie zmiany w wagach i odchyleniach.

Wzór na funkcję kosztu błędu średniokwadratowego to:

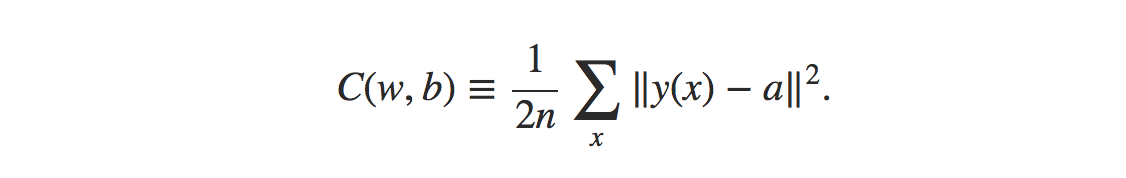
Źródło

Gdzie,

w = zbiór wag w sieci

b = stronniczość

n = liczba wejść treningowych

a = wektory wyjściowe

x = wejście

‖v‖ = zwykła długość wektora v

Funkcja strat w sieci neuronowej ze sprzężeniem do przodu

Funkcja strat w sieci neuronowej służy do określenia, czy istnieje jakaś poprawka, której wymaga proces uczenia.

Neurony warstwy wyjściowej będą równe liczbie klas. Porównanie różnicy między przewidywanym a rzeczywistym rozkładem prawdopodobieństwa.

Strata entropii krzyżowej dla klasyfikacji binarnej to:

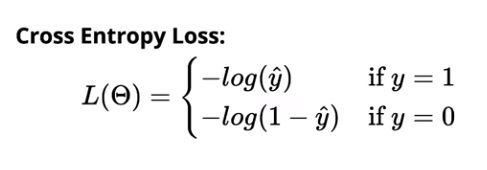
Strata entropii krzyżowej dla klasyfikacji wieloklasowej wynosi:

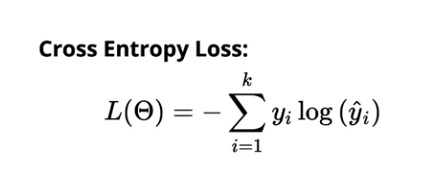
Źródło

Gradientowy algorytm uczenia się

Algorytm ten pomaga określić wszystkie najlepsze możliwe wartości parametrów w celu zmniejszenia strat w sieci neuronowej ze sprzężeniem do przodu.

Obraz

Wszystkie wagi (w₁₁₁, w₁₁₂,…) i błędy systematyczne b (b₁, b₂,….) są inicjowane losowo. Po wykonaniu tej czynności obserwacje w danych są powtarzane. Następnie odpowiedni przewidywany rozkład jest określany dla każdej obserwacji. Wreszcie strata jest obliczana za pomocą funkcji entropii krzyżowej.

Wartość strat pomaga następnie określić zmiany, jakie należy wprowadzić w wagach, aby zmniejszyć ogólną utratę modelu.

Przeczytaj: 13 interesujących pomysłów i tematów dotyczących projektów sieci neuronowych

Potrzeba modelu neuronowego

Załóżmy, że dane wejściowe podawane do sieci to surowe dane pikselowe pochodzące ze zeskanowanego obrazu postaci. Aby wynik w sieci poprawnie zaklasyfikował cyfrę, chciałbyś określić odpowiednią ilość wag i błędów systematycznych.

Teraz musiałbyś dokonać małych zmian w wadze w sieci, aby zobaczyć, jak działa uczenie. Aby to się udało, niewielkie zmiany wag powinny prowadzić tylko do niewielkich zmian w wydajności.

Co jednak, jeśli mała zmiana masy sprowadza się do dużej zmiany w produkcji? Model neuronu sigmoidalnego może rozwiązać ten problem.

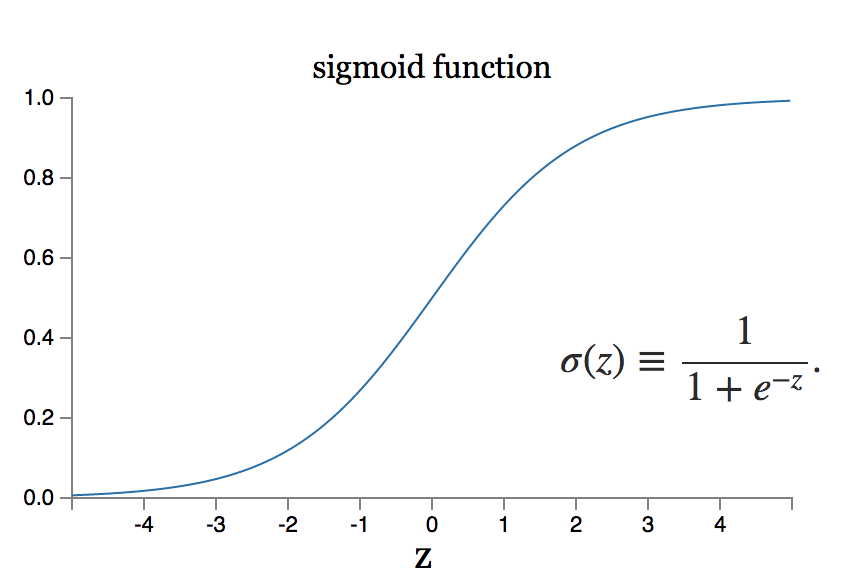
Źródło

Przeczytaj także: 7 rodzajów sztucznych sieci neuronowych, których potrzebują inżynierowie ML

Wniosek

Głębokie uczenie to obszar inżynierii oprogramowania z ogromnym zakresem badań. Istnieje wiele architektur sieci neuronowych zaktualizowanych dla różnych typów danych. Na przykład splotowe systemy neuronowe osiągnęły najlepsze w swojej klasie wykonanie w dziedzinie procedur obsługi obrazów, podczas gdy układy neuronowe rekurencyjne są zwykle wykorzystywane w przetwarzaniu treści i głosu.

W momencie zastosowania do ogromnych zbiorów danych, systemy neuronowe wymagają monstrualnych pomiarów siły obliczeniowej i przyspieszenia sprzętu, co można osiągnąć poprzez projektowanie rozmieszczenia jednostek przetwarzania grafiki lub procesorów graficznych. Jeśli dopiero zaczynasz korzystać z procesorów graficznych, możesz odkryć bezpłatne skonfigurowane ustawienia w Internecie. Najbardziej preferowane to Notatniki Kaggle lub Notatniki Google Collab.

Aby uzyskać efektywną sieć neuronową ze sprzężeniem do przodu, należy wykonać kilka iteracji w architekturze sieci, która wymaga wielu testów.

Aby uzyskać więcej informacji na temat działania tych sieci, ucz się od ekspertów z upGrad. Nasze kursy są niezwykle wszechstronne i możesz odpowiedzieć na swoje pytania, kontaktując się bezpośrednio z naszymi doświadczonymi i najlepszymi w swojej klasie nauczycielami.

Jeśli chcesz dowiedzieć się więcej o uczeniu maszynowym, sprawdź dyplom PG IIIT-B i upGrad w uczeniu maszynowym i sztucznej inteligencji, który jest przeznaczony dla pracujących profesjonalistów i oferuje ponad 450 godzin rygorystycznego szkolenia, ponad 30 studiów przypadków i zadań, IIIT- Status absolwenta B, ponad 5 praktycznych, praktycznych projektów zwieńczenia i pomoc w pracy z najlepszymi firmami.