前馈神经网络简介：层、功能和重要性

深度学习技术是搜索引擎、机器翻译和移动应用程序的支柱。 它通过模仿人脑从不同类型的数据中查找和创建模式来工作。

这项令人难以置信的技术的一个重要部分是前馈神经网络，它可以帮助软件工程师进行模式识别和分类、非线性回归和函数逼近。

让我们深入了解核心神经网络架构的这一重要方面。

什么是前馈神经网络？

前馈神经网络通常被称为多层神经元网络，之所以这样称呼，是因为所有信息仅在前向传播。

信息首先进入输入节点，穿过隐藏层，最后通过输出节点出来。 网络不包含将输出节点输出的信息反馈回网络的连接。

前馈神经网络旨在逼近函数。

这是它的工作原理。

有一个分类器 y = f*(x)。

这会将输入 x 输入到类别 y 中。

前馈网络将映射 y = f (x; θ)。 然后它会记住最接近函数的 θ 值。

前馈神经网络，用于图像中对象识别的基础，您可以在 Google 照片应用中发现。

前馈神经网络的层

前馈神经网络由以下部分组成。

输入层

它包含输入接收神经元。 然后他们将输入传递到下一层。 输入层的神经元总数等于数据集中的属性。

隐藏层

这是中间层，隐藏在输入和输出层之间。 这一层中有大量神经元对输入进行转换。 然后他们将其传递给输出层。

输出层

它是最后一层，取决于模型的构建。 此外，输出层是预测的特征，因为您知道您想要的结果是什么。

神经元权重

神经元之间连接的强度称为权重。 权重的取值范围为 0 到 1。

了解更多：神经网络模型：简介、词汇表

前馈神经网络中的成本函数

选择成本函数是前馈神经网络中最重要的部分之一。 通常，权重和偏差的微小变化不会影响分类数据点。 因此，要找出一种通过使用平滑成本函数对权重和偏差进行微小更改来提高性能的方法。

均方误差成本函数的公式为：

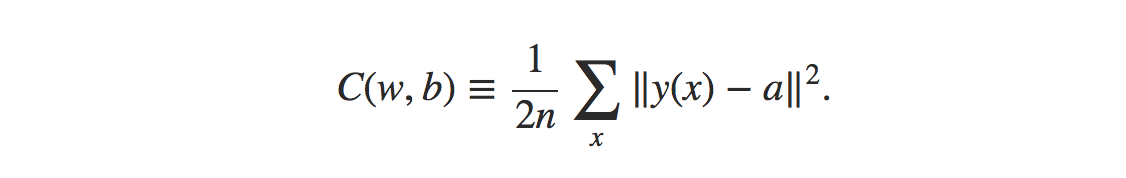
资源

在哪里，

w = 网络中权重的集合

b = 偏差

n = 训练输入数

a = 输出向量

x = 输入

‖v‖ = 向量 v 的通常长度

前馈神经网络中的损失函数

神经网络中的损失函数用于确定学习过程是否需要任何校正。

输出层神经元将等于类的数量。 比较预测和真实概率分布之间的差异。

二元分类的交叉熵损失为：

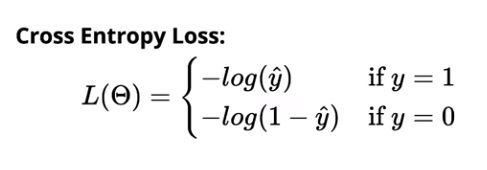
多类分类的交叉熵损失为：

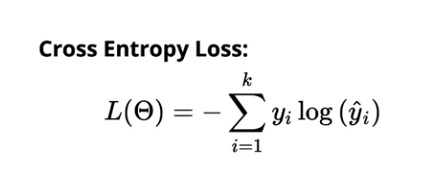
资源

梯度学习算法

该算法有助于确定参数的所有最佳可能值，以减少前馈神经网络中的损失。

图片

所有的权重 (w111, w112,…) 和偏置 b (b1, b2,….) 都是随机初始化的。 完成此操作后，将迭代数据中的观察结果。 然后，针对每个观察确定相应的预测分布。 最后，使用交叉熵函数计算损失。

然后，损失值有助于计算权重的变化，以减少模型的整体损失。

阅读： 13 个有趣的神经网络项目想法和主题

对神经元模型的需求

假设输入网络的输入是来自字符扫描图像的原始像素数据。 为了使网络中的输出正确分类数字，您需要确定正确的权重和偏差量。

现在，您需要对网络中的权重进行小幅更改，看看学习是如何进行的。 为了完美地实现这一点，权重的微小变化只会导致输出的微小变化。

但是，如果权重的微小变化相当于输出的大变化怎么办？ sigmoid 神经元模型可以解决这样的问题。

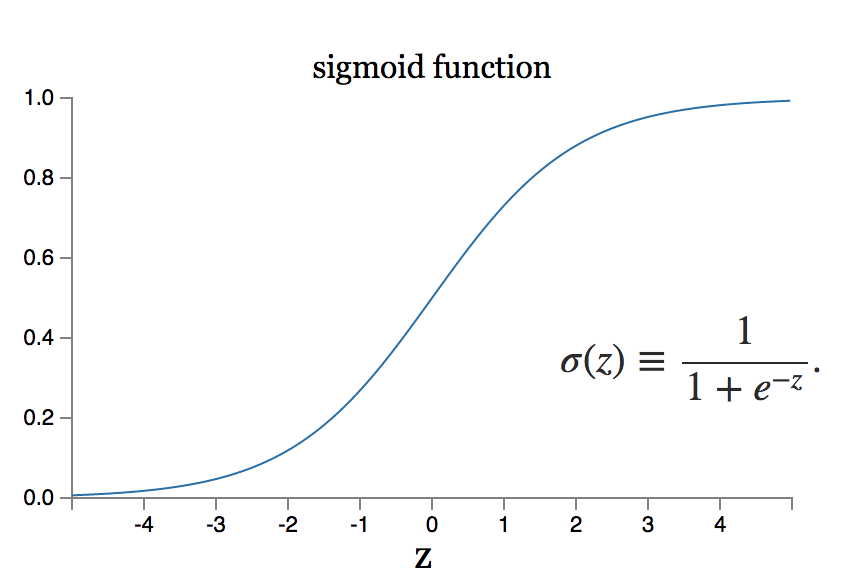
资源

另请阅读： ML 工程师需要的 7 种人工神经网络

结论

深度学习是软件工程的一个领域，研究范围很广。 有许多针对各种数据类型实现的神经网络架构。 例如，卷积神经系统在图像处理程序领域实现了最佳执行，而循环神经系统通常用于内容和语音处理。

当应用于庞大的数据集时，神经系统需要计算力和设备加速的巨大测量，这可以通过布置图形处理单元或 GPU 的设计来实现。 如果您不熟悉使用 GPU，您可以在 Web 上找到免费的配置设置。 最受欢迎的是 Kaggle Notebooks 或 Google Collab Notebooks。

要实现有效的前馈神经网络，您需要在网络架构中执行多次迭代，这需要大量测试。

有关这些网络如何工作的更多信息，请向 upGrad 的专家学习。 我们的课程非常全面，您可以通过直接与我们经验丰富且一流的教师联系来解决您的疑问。

如果您有兴趣了解有关机器学习的更多信息，请查看 IIIT-B 和 upGrad 的机器学习和人工智能 PG 文凭，该文凭专为工作专业人士设计，提供 450 多个小时的严格培训、30 多个案例研究和作业、IIIT- B 校友身份、5 个以上实用的实践顶点项目和顶级公司的工作协助。