Uma Introdução à Rede Neural Feedforward: Camadas, Funções e Importância
Publicados: 2020-05-28A tecnologia de aprendizado profundo é a espinha dorsal dos mecanismos de pesquisa, tradução automática e aplicativos móveis. Ele funciona imitando o cérebro humano para encontrar e criar padrões a partir de diferentes tipos de dados.
Uma parte importante dessa tecnologia incrível é uma rede neural feedforward, que auxilia os engenheiros de software no reconhecimento e classificação de padrões, regressão não linear e aproximação de funções.
Vamos obter alguns insights sobre esse aspecto essencial da arquitetura de rede neural central.
Índice
O que é Rede Neural Feedforward?
Comumente conhecidas como uma rede de neurônios de várias camadas, as redes neurais feedforward são chamadas assim devido ao fato de que todas as informações viajam apenas na direção direta.
A informação primeiro entra nos nós de entrada, move-se pelas camadas ocultas e, finalmente, sai pelos nós de saída. A rede não contém conexões para alimentar as informações que saem do nó de saída de volta à rede.
As redes neurais feedforward destinam-se a aproximar funções.

Aqui está como funciona .
Existe um classificador y = f*(x).
Isso alimenta a entrada x na categoria y.
A rede feedforward mapeará y = f (x; θ). Em seguida, ele memoriza o valor de θ que melhor se aproxima da função.
Rede neural feedforward para a base para reconhecimento de objetos em imagens, como você pode ver no aplicativo Google Fotos.
As camadas de uma rede neural feedforward
Uma rede neural feedforward consiste no seguinte.
Camada de entrada
Ele contém os neurônios receptores de entrada. Eles então passam a entrada para a próxima camada. O número total de neurônios na camada de entrada é igual aos atributos no conjunto de dados.
Camada oculta
Esta é a camada intermediária, escondida entre as camadas de entrada e saída. Há um grande número de neurônios nesta camada que aplicam transformações nas entradas. Eles então o passam para a camada de saída.
Camada de saída
É a última camada e depende da construção do modelo. Além disso, a camada de saída é o recurso previsto, pois você sabe o que deseja que seja o resultado.
Pesos de neurônios
A força de uma conexão entre os neurônios é chamada de pesos. O valor de um peso varia de 0 a 1.
Saiba mais: Modelo de Rede Neural: Breve Introdução, Glossário
Função de custo na rede neural de feedforward
Escolher a função de custo é uma das partes mais importantes de uma rede neural feedforward. Normalmente, pequenas mudanças nos pesos e vieses não afetam os pontos de dados classificados. Então, para descobrir uma maneira de melhorar o desempenho usando uma função de custo suave para fazer pequenas alterações em pesos e vieses.
A fórmula para a função de custo do erro quadrático médio é:
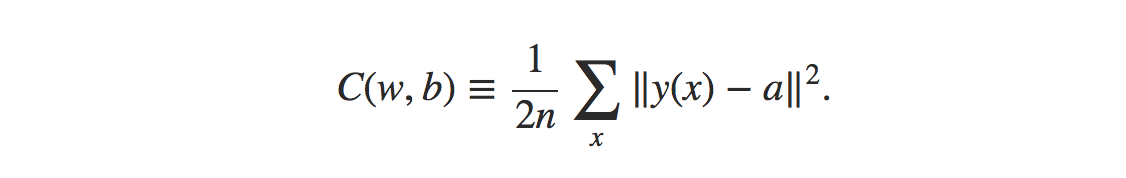
Fonte
Onde,
w = coleção de pesos na rede
b = preconceitos
n = número de entradas de treinamento
a = vetores de saída
x = entrada
‖v‖ = comprimento usual do vetor v
Função de perda na rede neural de feedforward
A função de perda na rede neural destina-se a determinar se há alguma correção que o processo de aprendizado precisa.
Os neurônios da camada de saída serão iguais ao número de classes. Comparar a diferença entre a distribuição de probabilidades prevista e verdadeira.
A perda de entropia cruzada para classificação binária é:
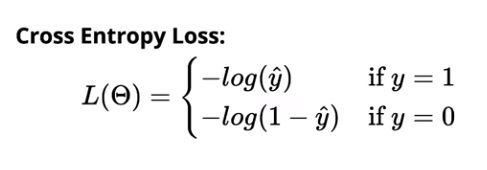
A perda de entropia cruzada para classificação multiclasse é:

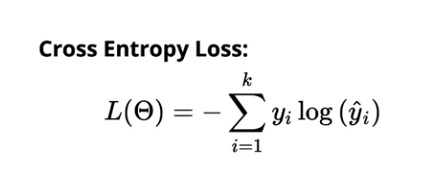
Fonte
Algoritmo de Aprendizagem Gradiente
Esse algoritmo ajuda a determinar todos os melhores valores possíveis para os parâmetros para diminuir a perda na rede neural feedforward.

Imagem
Todos os pesos (w₁₁₁, w₁₁₂,…) e bias b (b₁, b₂,….) são inicializados aleatoriamente. Uma vez feito isso, as observações nos dados são iteradas. Então, a distribuição prevista correspondente é determinada contra cada observação. Finalmente, a perda é calculada usando a função de entropia cruzada.
O valor de perda ajuda a calcular as alterações a serem feitas nos pesos para diminuir a perda geral do modelo.
Leia: 13 ideias e tópicos interessantes de projetos de redes neurais
A necessidade de um modelo de neurônio
Digamos que as entradas que estão sendo alimentadas na rede são dados brutos de pixel que vêm de uma imagem digitalizada de um personagem. Para que a saída na rede classifique o dígito corretamente, você deve determinar a quantidade certa de pesos e desvios.
Agora, você precisaria fazer pequenas alterações no peso na rede para ver como funcionaria o aprendizado. Para que isso ocorra perfeitamente, pequenas alterações nos pesos devem levar apenas a pequenas alterações na saída.
No entanto, e se a pequena mudança no peso equivaler a uma grande mudança na saída? O modelo do neurônio sigmóide pode resolver esse problema.
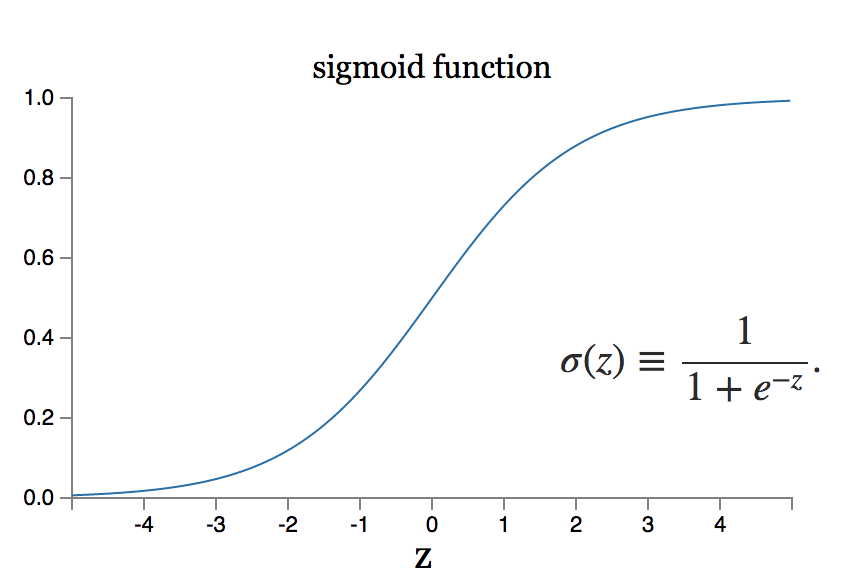
Fonte
Leia também: Os 7 tipos de redes neurais artificiais que os engenheiros de ML precisam

Conclusão
O aprendizado profundo é um território da engenharia de software com uma extensão colossal de pesquisa. Existem muitas arquiteturas de rede neural atualizadas para vários tipos de dados. Os sistemas neurais convolucionais, por exemplo, alcançaram a melhor execução da classe nos campos de procedimentos de manipulação de imagens, enquanto os sistemas neurais recorrentes são geralmente utilizados em conteúdo e processamento de voz.
No momento em que são aplicados a grandes conjuntos de dados, os sistemas neurais precisam de medidas monstruosas de força computacional e aceleração de equipamentos, que podem ser realizadas por meio do design de unidades de processamento gráfico ou GPUs. Se você é novo no uso de GPUs, pode encontrar configurações gratuitas na web. Os mais preferidos são Kaggle Notebooks ou Google Collab Notebooks.
Para realizar uma rede neural de feedforward eficaz, você executa várias iterações na arquitetura de rede, o que precisa de muitos testes.
Para obter mais informações sobre como essas redes funcionam, aprenda com os especialistas da upGrad. Nossos cursos são incrivelmente abrangentes e você pode resolver suas dúvidas entrando em contato diretamente com nossos professores experientes e melhores da classe.
Se você estiver interessado em aprender mais sobre aprendizado de máquina, confira o PG Diploma in Machine Learning & AI do IIIT-B e upGrad, projetado para profissionais que trabalham e oferece mais de 450 horas de treinamento rigoroso, mais de 30 estudos de caso e atribuições, IIIT- B Status de ex-aluno, mais de 5 projetos práticos práticos e assistência de trabalho com as principais empresas.
A álgebra linear é necessária em redes neurais?
Uma rede neural é um modelo matemático que resolve qualquer problema complexo. A rede pega um conjunto de entradas e calcula um conjunto de saídas com o objetivo de alcançar o resultado desejado. Ao estudar a teoria das redes neurais, a maioria dos neurônios e camadas são frequentemente formatados em álgebra linear. A álgebra linear é necessária para construir o modelo matemático. Você também pode usar álgebra linear para compreender a rede do modelo. Assim, para responder à pergunta, sim, o conhecimento básico de álgebra linear é obrigatório ao usar redes neurais.
O que se entende por retropropagação em redes neurais?
No caso de redes neurais que empregam gradiente descendente, a retropropagação é usada. Este algoritmo estima o gradiente da função de erro em relação aos pesos da rede neural e é essencialmente uma propagação inversa de erros. Essa abordagem é empregada porque o ajuste fino dos pesos reduz as taxas de erro e, portanto, melhora a generalização do modelo de rede neural, tornando-o mais confiável. A retropropagação é comumente categorizada como uma forma de aprendizado de máquina supervisionado, pois requer um resultado conhecido e pretendido para cada valor de entrada para calcular o gradiente da função de perda em redes neurais.
Como a retropropagação é diferente dos otimizadores?
Em redes neurais, são usados otimizadores e o algoritmo de retropropagação, que trabalham juntos para tornar o modelo mais confiável. A retropropagação é usada para calcular gradientes com eficiência e os otimizadores são usados para treinar a rede neural usando os gradientes obtidos usando a retropropagação. Em poucas palavras, o que a retropropagação faz por nós são gradientes de computação, que são posteriormente usados por otimizadores.
