Введение в нейронную сеть с прямой связью: уровни, функции и важность

Технология глубокого обучения лежит в основе поисковых систем, машинного перевода и мобильных приложений. Он работает, имитируя человеческий мозг, чтобы находить и создавать шаблоны из различных типов данных.

Одной из важных частей этой невероятной технологии является нейронная сеть с прямой связью, которая помогает разработчикам программного обеспечения в распознавании образов и классификации, нелинейной регрессии и аппроксимации функций.

Давайте рассмотрим этот важный аспект базовой архитектуры нейронной сети.

Что такое нейронная сеть с прямой связью?

Обычно известные как многослойная сеть нейронов, нейронные сети с прямой связью называются так из-за того, что вся информация передается только в прямом направлении.

Информация сначала поступает во входные узлы, проходит через скрытые слои и, наконец, выходит через выходные узлы. Сеть не содержит соединений для передачи информации, поступающей в выходной узел, обратно в сеть.

Нейронные сети с прямой связью предназначены для аппроксимации функций.

Вот как это работает .

Существует классификатор y = f*(x).

Это подает ввод x в категорию y.

Сеть прямой связи будет отображать y = f (x; θ). Затем он запоминает значение θ, которое лучше всего аппроксимирует функцию.

Нейронная сеть с прямой связью для основы распознавания объектов на изображениях, как вы можете заметить в приложении Google Фото.

Слои нейронной сети с прямой связью

Нейронная сеть с прямой связью состоит из следующего.

Входной слой

Он содержит нейроны, принимающие входные данные. Затем они передают ввод следующему слою. Общее количество нейронов во входном слое равно атрибутам в наборе данных.

Скрытый слой

Это средний слой, скрытый между входным и выходным слоями. В этом слое находится огромное количество нейронов, которые применяют преобразования к входным данным. Затем они передают его на выходной слой.

Выходной слой

Это последний слой, и он зависит от построения модели. Кроме того, выходной слой является прогнозируемой функцией, поскольку вы знаете, каким должен быть результат.

Вес нейронов

Сила связи между нейронами называется весами. Значение веса находится в диапазоне от 0 до 1.

Узнайте больше: модель нейронной сети: краткое введение, глоссарий

Функция стоимости в нейронной сети с прямой связью

Выбор функции стоимости является одной из наиболее важных частей нейронной сети с прямой связью. Обычно небольшие изменения весов и смещений не влияют на классифицированные точки данных. Итак, чтобы найти способ улучшить производительность, используя плавную функцию стоимости, чтобы внести небольшие изменения в веса и смещения.

Формула для функции стоимости среднеквадратичной ошибки:

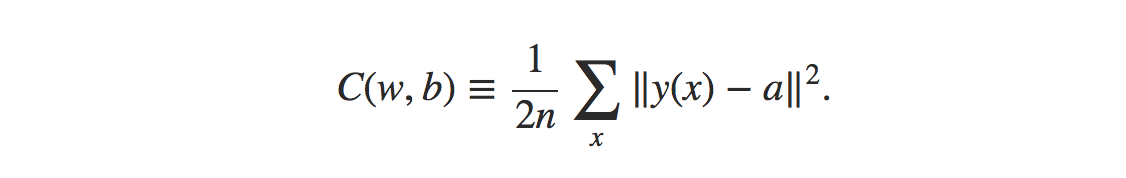
Источник

Где,

w = набор весов в сети

б = предубеждения

n = количество входных данных для обучения

а = выходные векторы

х = ввод

‖v‖ = обычная длина вектора v

Функция потерь в нейронной сети с прямой связью

Функция потерь в нейронной сети предназначена для определения необходимости корректировки процесса обучения.

Нейронов выходного слоя будет равно количеству классов. Сравнить разницу между предсказанным и истинным распределением вероятностей.

Перекрестная энтропийная потеря для бинарной классификации:

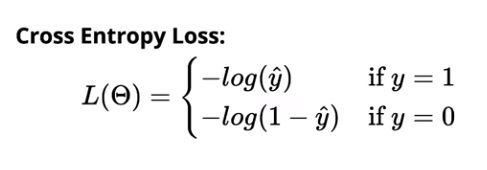
Перекрестная энтропийная потеря для многоклассовой классификации:

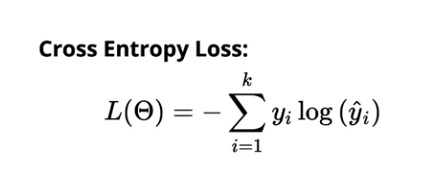
Источник

Алгоритм градиентного обучения

Этот алгоритм помогает определить все наилучшие возможные значения параметров, чтобы уменьшить потери в нейронной сети с прямой связью.

Изображение

Все веса (w₁₁₁, w₁₁₂,…) и смещения b (b₁, b₂,….) инициализируются случайным образом. Как только это будет сделано, наблюдения в данных повторяются. Затем для каждого наблюдения определяется соответствующее прогнозируемое распределение. Наконец, потери вычисляются с использованием кросс-энтропийной функции.

Затем значение потерь помогает вычислить изменения, которые необходимо внести в веса, чтобы уменьшить общие потери модели.

Читайте: 13 интересных идей и тем для проектов нейронных сетей

Потребность в нейронной модели

Допустим, входные данные, поступающие в сеть, представляют собой необработанные пиксельные данные, полученные из отсканированного изображения персонажа. Чтобы выходные данные в сети правильно классифицировали цифру, вам нужно определить правильное количество весов и смещений.

Теперь вам нужно будет внести небольшие изменения в вес в сети, чтобы посмотреть, как будет работать обучение. Чтобы это получилось идеально, небольшие изменения весов должны приводить только к небольшим изменениям на выходе.

Однако что, если небольшое изменение веса приводит к большому изменению объема производства? Модель сигмовидного нейрона может решить такую ​​проблему.

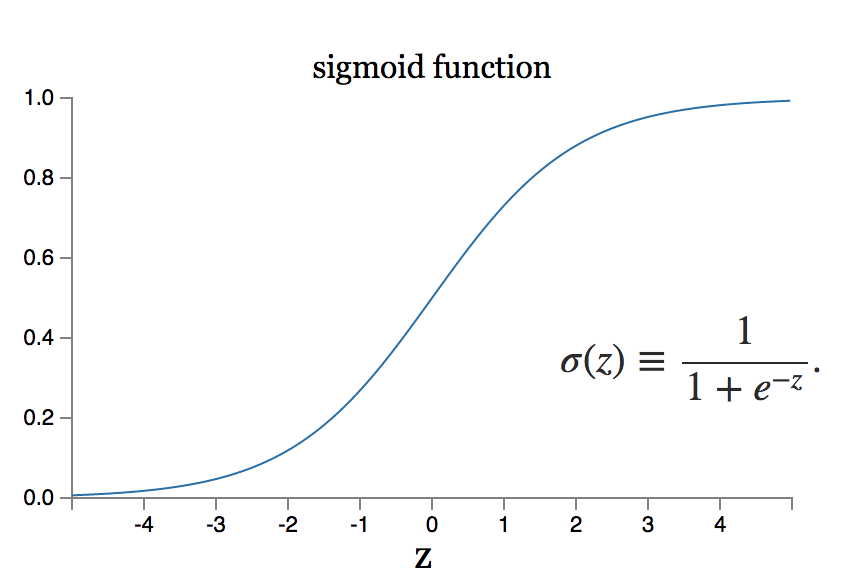
Источник

Читайте также: 7 типов искусственных нейронных сетей, которые нужны инженерам машинного обучения

Заключение

Глубокое обучение — это территория разработки программного обеспечения с колоссальным объемом исследований. Существует множество архитектур нейронных сетей, реализованных для различных типов данных. Сверточные нейронные системы, например, показали лучшие в своем классе результаты в области обработки изображений, в то время как рекуррентные нейронные системы обычно используются для обработки контента и голоса.

Применительно к огромным наборам данных нейронные системы нуждаются в чудовищных мерах вычислительной мощности и ускорения оборудования, что может быть достигнуто за счет дизайна размещения графических процессоров или графических процессоров. Если вы новичок в использовании графических процессоров, вы можете найти бесплатные настроенные параметры в Интернете. Наиболее предпочтительными из них являются блокноты Kaggle или блокноты Google Collab.

Чтобы создать эффективную нейронную сеть с прямой связью, вы выполняете несколько итераций сетевой архитектуры, что требует тщательного тестирования.

Для получения дополнительной информации о том, как работают эти сети, узнайте у экспертов upGrad. Наши курсы невероятно всеобъемлющи, и вы можете решить свои вопросы, напрямую связавшись с нашими опытными и лучшими в своем классе преподавателями.

Если вам интересно узнать больше о машинном обучении, ознакомьтесь с дипломом PG IIIT-B и upGrad в области машинного обучения и искусственного интеллекта, который предназначен для работающих профессионалов и предлагает более 450 часов тщательного обучения, более 30 тематических исследований и заданий, IIIT- Статус B Alumni, более 5 практических практических проектов и помощь в трудоустройстве в ведущих фирмах.