前饋神經網絡簡介：層、功能和重要性

深度學習技術是搜索引擎、機器翻譯和移動應用程序的支柱。 它通過模仿人腦從不同類型的數據中查找和創建模式來工作。

這項令人難以置信的技術的一個重要部分是前饋神經網絡，它可以幫助軟件工程師進行模式識別和分類、非線性回歸和函數逼近。

讓我們深入了解核心神經網絡架構的這一重要方面。

什麼是前饋神經網絡？

前饋神經網絡通常被稱為多層神經元網絡，之所以這樣稱呼，是因為所有信息僅在前向傳播。

信息首先進入輸入節點，穿過隱藏層，最後通過輸出節點出來。 網絡不包含將輸出節點輸出的信息反饋回網絡的連接。

前饋神經網絡旨在逼近函數。

這是它的工作原理。

有一個分類器 y = f*(x)。

這會將輸入 x 輸入到類別 y 中。

前饋網絡將映射 y = f (x; θ)。 然後它會記住最接近函數的 θ 值。

前饋神經網絡，用於圖像中對象識別的基礎，您可以在 Google 照片應用中發現。

前饋神經網絡的層

前饋神經網絡由以下部分組成。

輸入層

它包含輸入接收神經元。 然後他們將輸入傳遞到下一層。 輸入層的神經元總數等於數據集中的屬性。

隱藏層

這是中間層，隱藏在輸入和輸出層之間。 這一層中有大量神經元對輸入進行轉換。 然後他們將其傳遞給輸出層。

輸出層

它是最後一層，取決於模型的構建。 此外，輸出層是預測的特徵，因為您知道您想要的結果是什麼。

神經元權重

神經元之間連接的強度稱為權重。 權重的取值範圍為 0 到 1。

了解更多：神經網絡模型：簡介、詞彙表

前饋神經網絡中的成本函數

選擇成本函數是前饋神經網絡中最重要的部分之一。 通常，權重和偏差的微小變化不會影響分類數據點。 因此，要找出一種通過使用平滑成本函數對權重和偏差進行微小更改來提高性能的方法。

均方誤差成本函數的公式為：

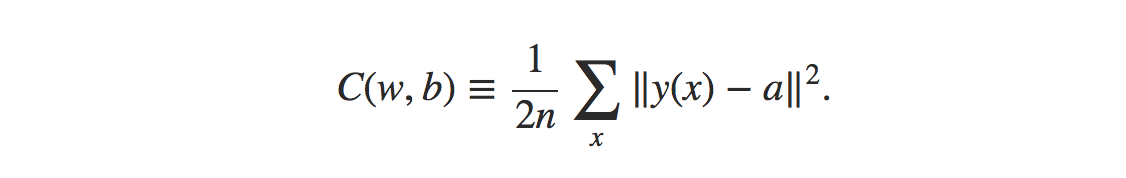
資源

在哪裡，

w = 網絡中權重的集合

b = 偏差

n = 訓練輸入數

a = 輸出向量

x = 輸入

‖v‖ = 向量 v 的通常長度

前饋神經網絡中的損失函數

神經網絡中的損失函數用於確定學習過程是否需要任何校正。

輸出層神經元將等於類的數量。 比較預測和真實概率分佈之間的差異。

二元分類的交叉熵損失為：

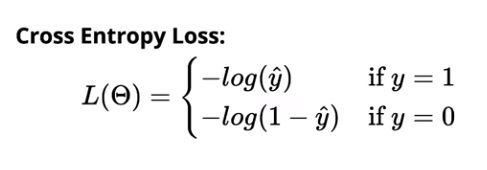
多類分類的交叉熵損失為：

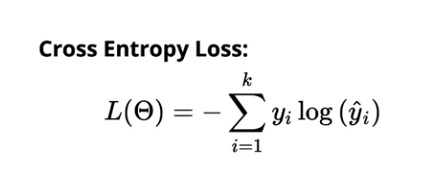
資源

梯度學習算法

該算法有助於確定參數的所有最佳可能值，以減少前饋神經網絡中的損失。

圖片

所有的權重 (w111, w112,…) 和偏置 b (b1, b2,….) 都是隨機初始化的。 完成此操作後，將迭代數據中的觀察結果。 然後，針對每個觀察確定相應的預測分佈。 最後，使用交叉熵函數計算損失。

然後，損失值有助於計算權重的變化，以減少模型的整體損失。

閱讀： 13 個有趣的神經網絡項目想法和主題

對神經元模型的需求

假設輸入網絡的輸入是來自字符掃描圖像的原始像素數據。 為了使網絡中的輸出正確分類數字，您需要確定正確的權重和偏差量。

現在，您需要對網絡中的權重進行小幅更改，看看學習是如何進行的。 為了完美地實現這一點，權重的微小變化只會導致輸出的微小變化。

但是，如果權重的微小變化相當於輸出的大變化怎麼辦？ sigmoid 神經元模型可以解決這樣的問題。

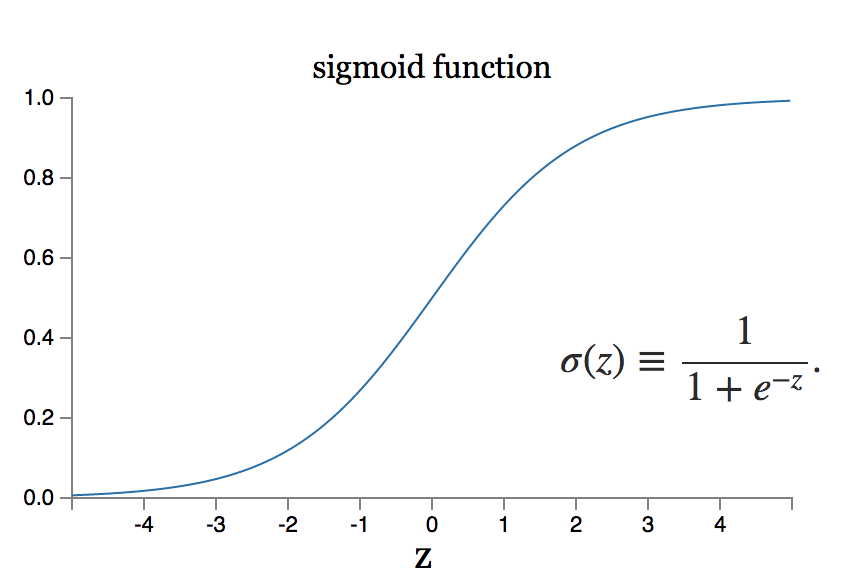
資源

另請閱讀： ML 工程師需要的 7 種人工神經網絡

結論

深度學習是軟件工程的一個領域，研究範圍很廣。 有許多針對各種數據類型實現的神經網絡架構。 例如，卷積神經系統在圖像處理程序領域實現了最佳執行，而循環神經系統通常用於內容和語音處理。

當應用於龐大的數據集時，神經系統需要計算力和設備加速的巨大測量，這可以通過佈置圖形處理單元或 GPU 的設計來實現。 如果您不熟悉使用 GPU，您可以在 Web 上找到免費的配置設置。 最受歡迎的是 Kaggle Notebooks 或 Google Collab Notebooks。

要實現有效的前饋神經網絡，您需要在網絡架構中執行多次迭代，這需要大量測試。

有關這些網絡如何工作的更多信息，請向 upGrad 的專家學習。 我們的課程非常全面，您可以通過直接與我們經驗豐富且一流的教師聯繫來解決您的疑問。

如果您有興趣了解有關機器學習的更多信息，請查看 IIIT-B 和 upGrad 的機器學習和人工智能 PG 文憑，該文憑專為工作專業人士設計，提供 450 多個小時的嚴格培訓、30 多個案例研究和作業、IIIT- B 校友身份、5 個以上實用的實踐頂點項目和頂級公司的工作協助。