5 tipuri de arbore binar explicate [cu ilustrații]

În informatică, diverse structuri de date ajută la aranjarea datelor în diferite forme. Printre acestea, arborii sunt structuri de date abstracte utilizate pe scară largă care simulează o structură arborescentă ierarhică. Un arbore are de obicei o valoare rădăcină și subarbori care sunt formați din nodurile copil din nodurile părinte. Arborii sunt structuri de date neliniare.

O structură generală de date arborescentă nu are nicio limitare în ceea ce privește numărul de noduri copii pe care le poate deține. Cu toate acestea, acesta nu este cazul unui arbore binar. Acest articol va afla despre o anumită structură de date arbore - arbore binar și tipuri de arbore binar .

Ce este structura de date a arborelui binar?

Un arbore binar este o structură de date neliniară de tip arbore cu maximum doi copii pentru fiecare părinte. Fiecare nod dintr-un arbore binar are o referință la stânga și la dreapta împreună cu elementul de date. Nodul din partea de sus a ierarhiei unui arbore se numește nodul rădăcină. Nodurile care dețin alte sub-noduri sunt nodurile părinte.

Un nod părinte are două noduri copil: copilul stâng și copilul drept. Hashing, rutarea datelor pentru traficul de rețea, compresia datelor, pregătirea heap-urilor binare și arborii de căutare binari sunt câteva dintre aplicațiile care folosesc un arbore binar.

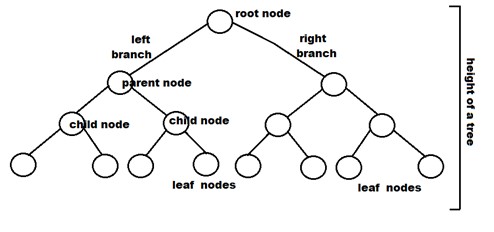
Terminologii asociate cu arbori binari și tipuri de arbori binari

• Nod: Reprezintă un punct de terminare într-un arbore.
• Rădăcină: cel mai înalt nod al copacului.
• Părinte: Fiecare nod (în afară de rădăcină) dintr-un arbore care are cel puțin un sub-nod propriu se numește nod părinte.
• Copil: Un nod care a venit imediat de la un nod părinte atunci când se îndepărtează de rădăcină este nodul copil.
• Leaf Node: Acestea sunt noduri externe. Sunt nodurile care nu au copii.
• Nodul intern: După cum sugerează și numele, acestea sunt noduri interioare cu cel puțin un copil.
• Adâncimea unui arbore: numărul de margini de la nodul arborelui până la rădăcină este.
• Înălțimea unui copac: este numărul de margini de la nod până la cea mai adâncă frunză. Înălțimea copacului este considerată și înălțimea rădăcinii.

Deoarece acum sunteți familiarizat cu terminologiile asociate cu arborele binar și tipurile de arbore binar, este timpul să înțelegeți componentele arborelui binar . Consultați cursurile noastre de știință a datelor pentru a afla în profunzime structura și componentele binare.

Componentele arborelui binar

Există trei componente ale arborelui binar . Fiecare nod de arbore binar are aceste trei componente asociate cu el. Devine un concept esențial pentru programatori să înțeleagă aceste trei componente ale arborelui binar:

1. Element de date
2. Indicator către subarborele din stânga
3. Indicatorul către subarborele din dreapta

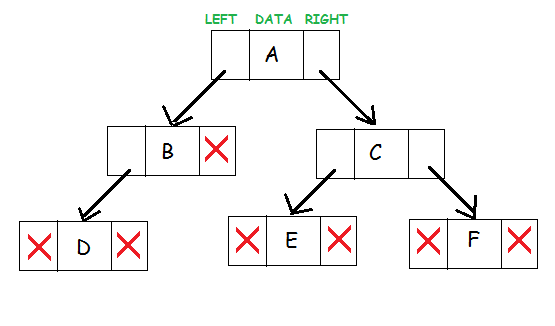
Sursă

Aceste trei componente ale arborelui binar reprezintă un nod. Datele se află în mijloc. Pointerul din stânga indică către nodul copil, formând sub-arborele din stânga. Pointerul din dreapta indică nodul copil din dreapta acestuia, creând subarborele din dreapta.

Citiți: Cele mai bune întrebări și metode informative pentru știința datelor

Tipuri de arbori binari

Există diferite tipuri de arbori binari și fiecare dintre aceste tipuri de arbori binari are caracteristici unice. Iată fiecare dintre tipurile de arbore binar în detaliu:

1. Arborele binar complet

Este un tip special de arbore binar care are fie zero copii, fie doi copii. Înseamnă că toate nodurile din acel arbore binar ar trebui fie să aibă două noduri copil ale nodului părinte, fie nodul părinte este el însuși nodul frunză sau nodul extern.

Cu alte cuvinte, un arbore binar complet este un arbore binar unic în care fiecare nod, cu excepția nodului extern, are doi copii. Când deține un singur copil, un astfel de arbore binar nu va fi un arbore binar complet. Aici, cantitatea de noduri de frunze este egală cu numărul de noduri interne plus unu. Ecuația este ca L=I+1, unde L este numărul de noduri frunză și I este numărul de noduri interne.

Iată structura unui arbore binar complet:

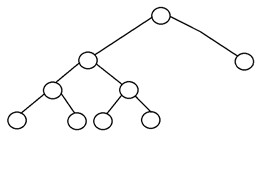
2. Arborele binar complet

Un arbore binar complet este un alt tip specific de arbore binar în care toate nivelurile arborelui sunt umplute în întregime cu noduri, cu excepția celui mai jos nivel al arborelui. De asemenea, în ultimul sau cel mai jos nivel al acestui arbore binar, fiecare nod ar trebui să se afle în partea stângă. Iată structura unui arbore binar complet:

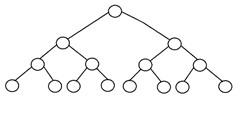
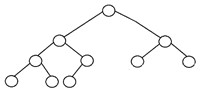
3. Arborele binar perfect

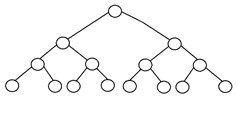
Se spune că un arbore binar este „perfect” dacă toate nodurile interne au strict doi copii și fiecare nod extern sau frunză este la același nivel sau aceeași adâncime în interiorul unui arbore. Un arbore binar perfect având înălțimea „h” are 2h – 1 nod. Iată structura unui arbore binar perfect:

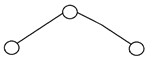
4. Arborele binar echilibrat

Se spune că un arbore binar este „echilibrat” dacă înălțimea arborelui este O(logN), unde „N” este numărul de noduri. Într-un arbore binar echilibrat, înălțimea subarborilor din stânga și din dreapta fiecărui nod ar trebui să varieze cu cel mult unu. Un arbore AVL și un arbore roșu-negru sunt câteva exemple comune de structură de date care pot genera un arbore de căutare binar echilibrat. Iată un exemplu de arbore binar echilibrat:

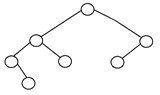
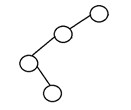
5. Arborele binar degenerat

Se spune că un arbore binar este un arbore binar degenerat sau un arbore binar patologic dacă fiecare nod intern are doar un singur copil. Astfel de arbori sunt similari cu o listă legată din punct de vedere al performanței. Iată un exemplu de arbore binar degenerat:

Beneficiile unui arbore binar

• Operația de căutare într-un arbore binar este mai rapidă în comparație cu alți arbori
• Doar două traversări sunt suficiente pentru a furniza elementele în ordine sortată
• Este ușor să ridicați elementele maxime și minime
• Traversarea graficelor folosește și arbori binari
• Conversia diferitelor expresii postfix și prefix este posibilă folosind arbori binari

Citește și: Arborele de decizie în învățarea automată: funcții, clasificare, avantaje și dezavantaje

Concluzie

Arborele binar este unul dintre cei mai folosiți arbori în structura datelor. Fiecare dintre tipurile de arbore binar are caracteristicile sale unice. Aceste structuri de date au cerințe specifice în informatica aplicată. Sperăm că acest articol despre tipurile de arbori binari a fost de ajutor. upGrad oferă diverse cursuri de știință a datelor, învățare automată, date mari și multe altele.

Dacă sunteți curios să aflați despre știința datelor, consultați programul Executive PG în știința datelor de la IIIT-B și upGrad, care este creat pentru profesioniști care lucrează și oferă peste 10 studii de caz și proiecte, ateliere practice practice, mentorat cu experți din industrie, 1 -on-1 cu mentori din industrie, peste 400 de ore de învățare și asistență profesională cu firme de top.