Объяснение 5 типов бинарного дерева [с иллюстрациями]

В компьютерных науках различные структуры данных помогают упорядочивать данные в разных формах. Среди них деревья — широко используемые абстрактные структуры данных, имитирующие иерархическую древовидную структуру. Дерево обычно имеет корневое значение и поддеревья, которые формируются дочерними узлами из его родительских узлов. Деревья — это нелинейные структуры данных.

Общая древовидная структура данных не имеет ограничений на количество дочерних узлов, которые она может содержать. Однако это не относится к бинарному дереву. В этой статье вы узнаете о конкретной древовидной структуре данных — бинарном дереве и типах бинарного дерева .

Что такое структура данных двоичного дерева?

Двоичное дерево — это нелинейная структура данных древовидного типа с максимум двумя дочерними элементами для каждого родителя. Каждый узел в бинарном дереве имеет левую и правую ссылку вместе с элементом данных. Узел на вершине иерархии дерева называется корневым узлом. Узлы, содержащие другие подузлы, являются родительскими узлами.

Родительский узел имеет два дочерних узла: левый дочерний и правый дочерний. Хеширование, маршрутизация данных для сетевого трафика, сжатие данных, подготовка двоичных куч и двоичные деревья поиска — вот некоторые из приложений, использующих двоичное дерево.

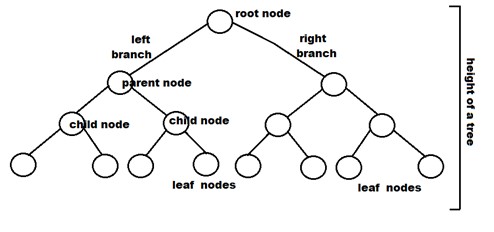
Терминологии, связанные с бинарными деревьями и типами бинарных деревьев

• Узел: представляет точку завершения в дереве.
• Корень: самый верхний узел дерева.
• Родитель: каждый узел (кроме корня) в дереве, который имеет хотя бы один собственный подузел, называется родительским узлом.
• Дочерний: узел, который сразу же вышел из родительского узла при удалении от корня, является дочерним узлом.
• Листовой узел: это внешние узлы. Это узлы, у которых нет потомков.
• Внутренний узел: как следует из названия, это внутренние узлы, по крайней мере, с одним дочерним элементом.
• Глубина дерева: количество ребер от узла дерева до корня.
• Высота дерева: это количество ребер от узла до самого глубокого листа. Высота дерева также считается высотой корня.

Поскольку вы уже знакомы с терминологией, связанной с бинарным деревом и типами бинарного дерева, пришло время понять компоненты бинарного дерева . Ознакомьтесь с нашими курсами по науке о данных, чтобы узнать больше о двоичной структуре и компонентах.

Компоненты бинарного дерева

Есть три компонента бинарного дерева . С каждым узлом бинарного дерева связаны эти три компонента. Для программистов становится важной концепцией понимания этих трех компонентов бинарного дерева:

1. Элемент данных
2. Указатель на левое поддерево
3. Указатель на правое поддерево

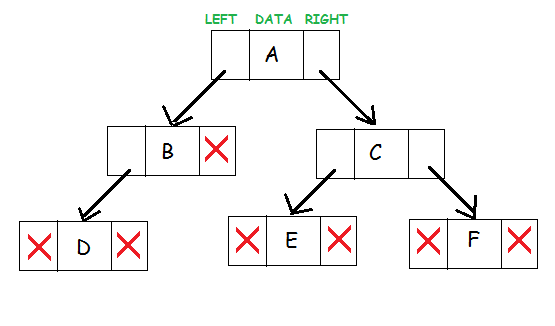
Источник

Эти три компонента бинарного дерева представляют узел. Данные находятся посередине. Левый указатель указывает на дочерний узел, формирующий левое поддерево. Правый указатель указывает на дочерний узел справа от него, создавая правое поддерево.

Читайте: Лучшие вопросы для предположений и информационные методы для науки о данных

Типы бинарных деревьев

Существуют различные типы бинарных деревьев , и каждый из этих типов бинарных деревьев имеет уникальные характеристики. Вот подробно о каждом из типов бинарных деревьев :

1. Полное бинарное дерево

Это особый вид бинарного дерева, у которого либо ноль потомков, либо два потомка. Это означает, что все узлы в этом двоичном дереве должны либо иметь два дочерних узла своего родительского узла, либо родительский узел сам является конечным узлом или внешним узлом.

Другими словами, полное бинарное дерево — это уникальное бинарное дерево, в котором каждый узел, кроме внешнего, имеет двух дочерних элементов. Когда оно содержит одного потомка, такое бинарное дерево не будет полным бинарным деревом. Здесь количество листовых узлов равно количеству внутренних узлов плюс один. Уравнение похоже на L=I+1, где L — количество листовых узлов, а I — количество внутренних узлов.

Вот структура полного бинарного дерева:

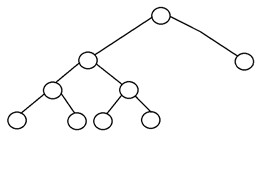
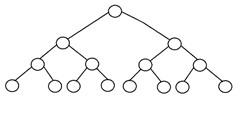
2. Полное бинарное дерево

Полное бинарное дерево — это еще один особый тип бинарного дерева, в котором все уровни дерева полностью заполнены узлами, кроме самого нижнего уровня дерева. Кроме того, на последнем или самом нижнем уровне этого бинарного дерева каждый узел, возможно, должен находиться на левой стороне. Вот структура полного бинарного дерева:

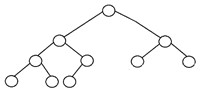
3. Идеальное бинарное дерево

Бинарное дерево называется «идеальным», если все внутренние узлы имеют строго двух дочерних элементов, и каждый внешний или листовой узел находится на одном уровне или на одной глубине внутри дерева. Идеальное бинарное дерево высотой h имеет 2h – 1 узел. Вот структура идеального бинарного дерева:

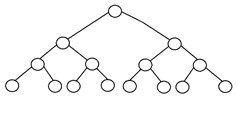
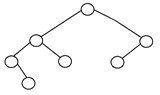
4. Сбалансированное бинарное дерево

Бинарное дерево называется «сбалансированным», если высота дерева равна O(logN), где N — количество узлов. В сбалансированном бинарном дереве высота левого и правого поддеревьев каждого узла должна отличаться не более чем на единицу. AVL-дерево и красно-черное дерево — некоторые распространенные примеры структуры данных, которые могут генерировать сбалансированное двоичное дерево поиска. Вот пример сбалансированного бинарного дерева:

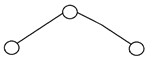
5. Вырожденное бинарное дерево

Бинарное дерево называется вырожденным бинарным деревом или патологическим бинарным деревом, если каждый внутренний узел имеет только одного потомка. Такие деревья по производительности аналогичны связным спискам. Вот пример вырожденного бинарного дерева:

Преимущества бинарного дерева

• Операция поиска в бинарном дереве выполняется быстрее по сравнению с другими деревьями.
• Достаточно всего двух обходов, чтобы предоставить элементы в отсортированном порядке.
• Легко подобрать максимальные и минимальные элементы
• Обход графа также использует бинарные деревья.
• Преобразование различных постфиксных и префиксных выражений возможно с использованием двоичных деревьев.

Читайте также: Деревья решений в машинном обучении: функции, классификация, плюсы и минусы

Заключение

Бинарное дерево является одним из наиболее широко используемых деревьев в структуре данных. Каждый из типов бинарных деревьев имеет свои уникальные особенности. Эти структуры данных предъявляют особые требования в прикладной информатике. Мы надеемся, что эта статья о типах бинарных деревьев была вам полезна. upGrad предлагает различные курсы по науке о данных, машинному обучению, большим данным и многому другому.

Если вам интересно узнать о науке о данных, ознакомьтесь с программой IIIT-B & upGrad Executive PG по науке о данных, которая создана для работающих профессионалов и предлагает более 10 тематических исследований и проектов, практические семинары, наставничество с отраслевыми экспертами, 1 -на-1 с отраслевыми наставниками, более 400 часов обучения и помощи в трудоустройстве в ведущих фирмах.