5種二叉樹解釋[附插圖]

在計算機科學中，各種數據結構有助於以不同形式排列數據。 其中，樹是一種廣泛使用的抽像數據結構，它模擬了層次樹結構。 樹通常具有根值和由其父節點的子節點形成的子樹。 樹是非線性數據結構。

一般的樹數據結構對它可以容納的子節點的數量沒有限制。 然而，這不是二叉樹的情況。 本文將學習一種特定的樹數據結構——二叉樹和二叉樹的類型。

什麼是二叉樹數據結構？

二叉樹是一種樹型非線性數據結構，每個父級最多有兩個子級。 二叉樹中的每個節點都有一個左右引用以及數據元素。 樹的層次結構頂部的節點稱為根節點。 擁有其他子節點的節點是父節點。

一個父節點有兩個子節點：左子節點和右子節點。 散列、網絡流量路由數據、數據壓縮、準備二叉堆和二叉搜索樹是使用二叉樹的一些應用程序。

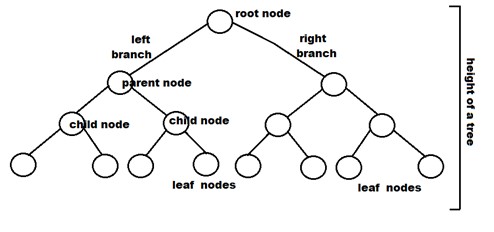
與二叉樹和二叉樹類型相關的術語

• 節點：它代表樹中的一個終止點。
• 根：樹的最頂層節點。
• 父節點：樹中的每個節點（除了根節點）至少有一個自己的子節點，稱為父節點。
• 子節點：當遠離根節點時直接來自父節點的節點是子節點。
• 葉節點：這些是外部節點。 它們是沒有子節點的節點。
• 內部節點：顧名思義，這些是具有至少一個孩子的內部節點。
• 樹的深度：從樹的節點到根的邊數。
• 樹的高度：它是從節點到最深葉子的邊數。 樹高也被認為是根高度。

現在您已經熟悉了與二叉樹和二叉樹類型相關的術語，是時候了解二叉樹組件了。 查看我們的數據科學課程，深入了解二進制結構和組件。

二叉樹組件

有三個二叉樹組件。 每個二叉樹節點都有這三個與之關聯的組件。 理解這三個二叉樹組件成為程序員的基本概念：

1. 數據元素
2. 指向左子樹的指針
3. 指向右子樹的指針

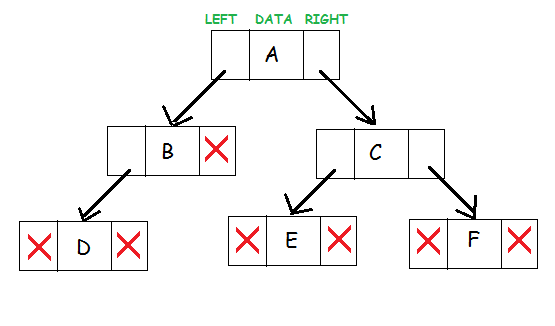
資源

這三個二叉樹組件代表一個節點。 數據位於中間。 左指針指向子節點，形成左子樹。 右指針指向其右邊的子節點，創建右子樹。

閱讀：數據科學的熱門猜測問題和信息方法

二叉樹的類型

二叉樹有多種類型，每種二叉樹類型都有其獨特的特徵。 以下是每種二叉樹類型的詳細信息：

1. 全二叉樹

它是一種特殊的二叉樹，有零個孩子或兩個孩子。 這意味著該二叉樹中的所有節點都應該具有其父節點的兩個子節點，或者父節點本身就是葉節點或外部節點。

換句話說，完整二叉樹是唯一的二叉樹，其中除了外部節點之外的每個節點都有兩個孩子。 當它只有一個孩子時，這樣的二叉樹將不是完整的二叉樹。 這裡，葉子節點的數量等於內部節點的數量加一。 這個方程就像L=I+1，其中 L 是葉節點的數量，I 是內部節點的數量。

下面是完整二叉樹的結構：

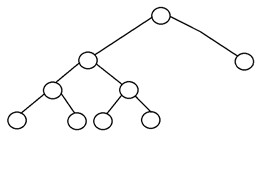
2. 完全二叉樹

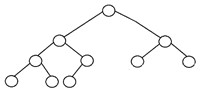
完全二叉樹是另一種特定類型的二叉樹，其中除了樹的最低層之外，所有樹層都完全用節點填充。 此外，在這棵二叉樹的最後一層或最低層中，每個節點都可能位於左側。 完整二叉樹的結構如下：

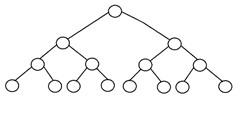
3. 完美二叉樹

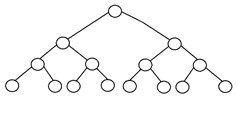
如果所有內部節點都有嚴格的兩個子節點，並且每個外部節點或葉節點在樹中處於相同級別或相同深度，則稱二叉樹是“完美的”。 高度為“h”的完美二叉樹有 2h – 1 個節點。 下面是完美二叉樹的結構：

4.平衡二叉樹

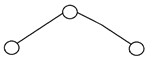
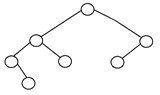
如果樹高為 O(logN)，則稱二叉樹是“平衡的”，其中“N”是節點數。 在平衡二叉樹中，每個節點的左右子樹的高度最多相差一個。 AVL 樹和紅黑樹是可以生成平衡二叉搜索樹的數據結構的一些常見示例。 下面是一個平衡二叉樹的例子：

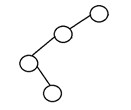
5. 退化二叉樹

如果每個內部節點只有一個子節點，則稱二叉樹為退化二叉樹或病態二叉樹。 這樣的樹在性能方麵類似於鍊錶。 下面是一個退化二叉樹的例子：

二叉樹的好處

• 與其他樹相比，二叉樹中的搜索操作更快
• 只需兩次遍歷就足以按排序順序提供元素
• 很容易拿起最大和最小的元素
• 圖遍歷也使用二叉樹
• 使用二叉樹可以轉換不同的後綴和前綴表達式

另請閱讀：機器學習中的決策樹：功能、分類、優缺點

結論

二叉樹是數據結構中使用最廣泛的樹之一。 每種二叉樹類型都有其獨特的特徵。 這些數據結構在應用計算機科學中有特定的要求。 我們希望這篇關於二叉樹類型的文章對您有所幫助。 upGrad 提供數據科學、機器學習、大數據等方面的各種課程。

如果您想了解數據科學，請查看 IIIT-B 和 upGrad 的數據科學執行 PG 計劃，該計劃是為在職專業人士創建的，提供 10 多個案例研究和項目、實用的實踐研討會、與行業專家的指導、1與行業導師一對一，400 多個小時的學習和頂級公司的工作協助。