5 types d'arbre binaire expliqués [avec illustrations]

En informatique, diverses structures de données aident à organiser les données sous différentes formes. Parmi eux, les arbres sont des structures de données abstraites largement utilisées qui simulent une structure arborescente hiérarchique. Un arbre a généralement une valeur racine et des sous-arbres qui sont formés par les nœuds enfants à partir de ses nœuds parents. Les arbres sont des structures de données non linéaires.

Une structure de données arborescente générale n'a aucune limitation quant au nombre de nœuds enfants qu'elle peut contenir. Or, ce n'est pas le cas avec un arbre binaire. Cet article va en apprendre davantage sur une structure de données arborescente spécifique - arbre binaire et types d'arbre binaire .

Qu'est-ce que la structure de données d'arbre binaire ?

Un arbre binaire est une structure de données non linéaire de type arbre avec un maximum de deux enfants pour chaque parent. Chaque nœud d'un arbre binaire a une référence gauche et droite avec l'élément de données. Le nœud au sommet de la hiérarchie d'un arbre est appelé le nœud racine. Les nœuds qui contiennent d'autres sous-nœuds sont les nœuds parents.

Un nœud parent a deux nœuds enfants : l'enfant gauche et l'enfant droit. Le hachage, le routage des données pour le trafic réseau, la compression des données, la préparation des tas binaires et les arbres de recherche binaires sont quelques-unes des applications qui utilisent un arbre binaire.

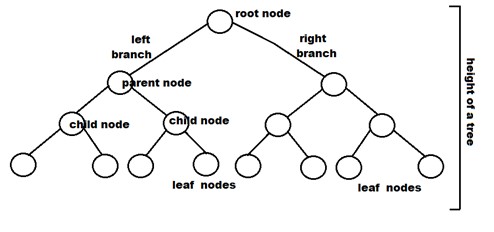
Terminologies associées aux arbres binaires et aux types d'arbres binaires

• Nœud : Il représente un point de terminaison dans un arbre.
• Racine : le nœud le plus élevé d'un arbre.
• Parent : chaque nœud (à l'exception de la racine) d'un arbre qui possède au moins un sous-nœud qui lui est propre est appelé un nœud parent.
• Enfant : un nœud qui vient directement d'un nœud parent en s'éloignant de la racine est le nœud enfant.
• Nœud feuille : il s'agit de nœuds externes. Ce sont les nœuds qui n'ont pas d'enfant.
• Nœud interne : comme son nom l'indique, ce sont des nœuds internes avec au moins un enfant.
• Profondeur d'un arbre : le nombre d'arêtes entre le nœud de l'arbre et la racine est.
• Hauteur d'un arbre : C'est le nombre d'arêtes du nœud à la feuille la plus profonde. La hauteur de l'arbre est également considérée comme la hauteur des racines.

Comme vous êtes maintenant familiarisé avec les terminologies associées à l'arbre binaire et aux types d'arbre binaire, il est temps de comprendre les composants de l'arbre binaire . Consultez nos cours de science des données pour en savoir plus sur la structure et les composants binaires.

Composants de l'arborescence binaire

Il existe trois composants d'arborescence binaire . Chaque nœud d'arbre binaire est associé à ces trois composants. Il devient un concept essentiel pour les programmeurs de comprendre ces trois composants de l'arbre binaire :

1. Élément de données
2. Pointeur vers le sous-arbre gauche
3. Pointeur vers le sous-arbre droit

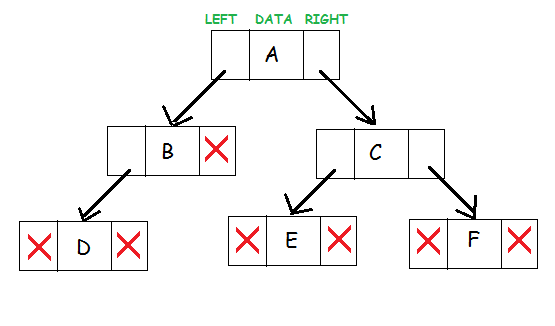
La source

Ces trois composants d'arbre binaire représentent un nœud. Les données résident au milieu. Le pointeur gauche pointe vers le nœud enfant, formant le sous-arbre gauche. Le pointeur droit pointe vers le nœud enfant à sa droite, créant le sous-arbre droit.

Lire : Principales questions d'estimation et méthodes informatives pour la science des données

Types d'arbres binaires

Il existe différents types d'arbres binaires , et chacun de ces types d'arbres binaires a des caractéristiques uniques. Voici chacun des types d'arbres binaires en détail :

1. Arbre binaire complet

C'est un type particulier d'arbre binaire qui a soit zéro enfant, soit deux enfants. Cela signifie que tous les nœuds de cet arbre binaire doivent avoir deux nœuds enfants de son nœud parent ou que le nœud parent est lui-même le nœud feuille ou le nœud externe.

En d'autres termes, un arbre binaire complet est un arbre binaire unique où chaque nœud, à l'exception du nœud externe, a deux enfants. Lorsqu'il contient un seul enfant, un tel arbre binaire ne sera pas un arbre binaire complet. Ici, la quantité de nœuds feuilles est égale au nombre de nœuds internes plus un. L'équation est comme L = I + 1, où L est le nombre de nœuds feuilles et I est le nombre de nœuds internes.

Voici la structure d'un arbre binaire complet :

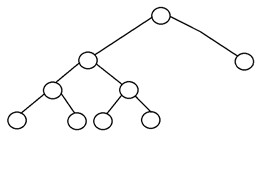
2. Arbre binaire complet

Un arbre binaire complet est un autre type spécifique d'arbre binaire où tous les niveaux de l'arbre sont entièrement remplis de nœuds, à l'exception du niveau le plus bas de l'arbre. De plus, dans le dernier ou le plus bas niveau de cet arbre binaire, chaque nœud devrait éventuellement résider sur le côté gauche. Voici la structure d'un arbre binaire complet :

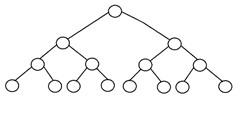
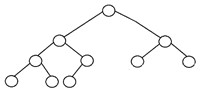
3. Arbre binaire parfait

Un arbre binaire est dit "parfait" si tous les nœuds internes ont strictement deux enfants, et chaque nœud externe ou feuille est au même niveau ou à la même profondeur dans un arbre. Un arbre binaire parfait de hauteur 'h' a 2h – 1 nœud. Voici la structure d'un arbre binaire parfait :

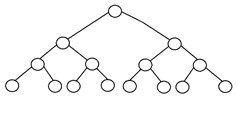
4. Arbre binaire équilibré

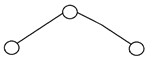
Un arbre binaire est dit « équilibré » si la hauteur de l'arbre est O(logN), où « N » est le nombre de nœuds. Dans un arbre binaire équilibré, la hauteur des sous-arbres gauche et droit de chaque nœud doit varier d'au plus un. Un arbre AVL et un arbre rouge-noir sont des exemples courants de structure de données pouvant générer un arbre de recherche binaire équilibré. Voici un exemple d'arbre binaire équilibré :

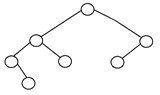
5. Arbre binaire dégénéré

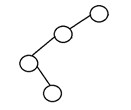
Un arbre binaire est dit arbre binaire dégénéré ou arbre binaire pathologique si chaque nœud interne n'a qu'un seul enfant. De tels arbres sont similaires à une liste chaînée en termes de performances. Voici un exemple d'arbre binaire dégénéré :

Avantages d'un arbre binaire

• L'opération de recherche dans un arbre binaire est plus rapide par rapport aux autres arbres
• Seuls deux parcours suffisent pour fournir les éléments dans un ordre trié
• Il est facile de ramasser les éléments maximum et minimum
• La traversée de graphe utilise également des arbres binaires
• La conversion de différentes expressions de suffixe et de préfixe est possible à l'aide d'arbres binaires

Lisez aussi : Arbres de décision dans l'apprentissage automatique : fonctions, classification, avantages et inconvénients

Conclusion

L'arbre binaire est l'un des arbres les plus utilisés dans la structure de données. Chacun des types d'arbres binaires a ses caractéristiques uniques. Ces structures de données ont des exigences spécifiques en informatique appliquée. Nous espérons que cet article sur les types d'arbres binaires vous a été utile. upGrad propose divers cours en science des données, en apprentissage automatique, en mégadonnées, etc.

Si vous êtes curieux d'en savoir plus sur la science des données, consultez le programme Executive PG en science des données de IIIT-B & upGrad qui est créé pour les professionnels en activité et propose plus de 10 études de cas et projets, des ateliers pratiques, un mentorat avec des experts de l'industrie, 1 -on-1 avec des mentors de l'industrie, plus de 400 heures d'apprentissage et d'aide à l'emploi avec les meilleures entreprises.