5 Arten von Binärbäumen erklärt [mit Illustrationen]

In der Informatik helfen verschiedene Datenstrukturen dabei, Daten in unterschiedlichen Formen anzuordnen. Darunter sind Bäume weit verbreitete abstrakte Datenstrukturen, die eine hierarchische Baumstruktur simulieren. Ein Baum hat normalerweise einen Wurzelwert und Unterbäume, die durch die untergeordneten Knoten seiner übergeordneten Knoten gebildet werden. Bäume sind nichtlineare Datenstrukturen.

Eine allgemeine Baumdatenstruktur hat keine Beschränkung hinsichtlich der Anzahl von untergeordneten Knoten, die sie aufnehmen kann. Dies ist jedoch bei einem binären Baum nicht der Fall. In diesem Artikel erfahren Sie mehr über eine bestimmte Baumdatenstruktur – Binärbaum und Arten von Binärbäumen .

Was ist eine binäre Baumdatenstruktur?

Ein Binärbaum ist eine nichtlineare Datenstruktur vom Baumtyp mit maximal zwei Kindern für jeden Elternteil. Jeder Knoten in einem Binärbaum hat zusammen mit dem Datenelement eine linke und eine rechte Referenz. Der Knoten an der Spitze der Hierarchie eines Baums wird Wurzelknoten genannt. Die Knoten, die andere Unterknoten enthalten, sind die übergeordneten Knoten.

Ein Elternknoten hat zwei Kindknoten: das linke Kind und das rechte Kind. Hashing, Routing von Daten für den Netzwerkverkehr, Datenkomprimierung, Vorbereitung binärer Heaps und binäre Suchbäume sind einige der Anwendungen, die einen binären Baum verwenden.

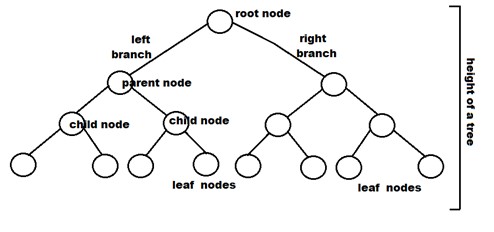
Terminologien im Zusammenhang mit Binärbäumen und Arten von Binärbäumen

• Knoten: Er repräsentiert einen Endpunkt in einem Baum.
• Wurzel: Der oberste Knoten eines Baums.
• Parent: Jeder Knoten (außer der Wurzel) in einem Baum, der mindestens einen eigenen Unterknoten hat, wird als Parent-Knoten bezeichnet.
• Kind: Ein Knoten, der direkt von einem Elternknoten kam, als er sich von der Wurzel wegbewegte, ist der Kindknoten.
• Blattknoten: Dies sind externe Knoten. Sie sind die Knoten, die kein Kind haben.
• Interner Knoten: Wie der Name schon sagt, sind dies innere Knoten mit mindestens einem Kind.
• Tiefe eines Baums: Die Anzahl der Kanten vom Knoten des Baums bis zur Wurzel ist.
• Höhe eines Baumes: Es ist die Anzahl der Kanten vom Knoten bis zum tiefsten Blatt. Die Baumhöhe gilt auch als Wurzelhöhe.

Da Sie nun mit den Terminologien im Zusammenhang mit dem Binärbaum und den Arten von Binärbäumen vertraut sind, ist es an der Zeit, die Komponenten des Binärbaums zu verstehen . Sehen Sie sich unsere Data-Science-Kurse an, um mehr über binäre Strukturen und Komponenten zu erfahren.

Binäre Baumkomponenten

Es gibt drei binäre Baumkomponenten . Jedem binären Baumknoten sind diese drei Komponenten zugeordnet. Es wird zu einem wesentlichen Konzept für Programmierer, diese drei binären Baumkomponenten zu verstehen:

1. Datenelement
2. Zeiger auf linken Teilbaum
3. Zeiger auf rechten Teilbaum

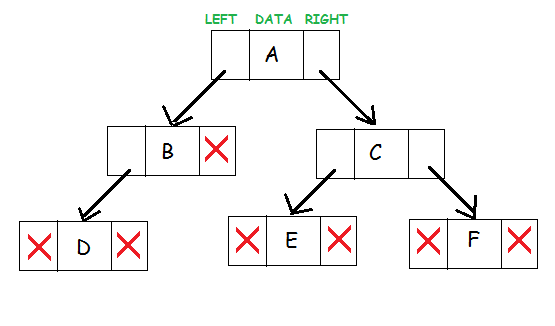
Quelle

Diese drei binären Baumkomponenten repräsentieren einen Knoten. Die Daten befinden sich in der Mitte. Der linke Zeiger zeigt auf den untergeordneten Knoten und bildet den linken Teilbaum. Der rechte Zeiger zeigt auf den untergeordneten Knoten rechts von ihm, wodurch der rechte Teilbaum erstellt wird.

Lesen Sie: Top Guesstimate Questions & Informative Methods for Data Science

Arten von Binärbäumen

Es gibt verschiedene Typen von Binärbäumen , und jeder dieser Binärbaumtypen hat einzigartige Eigenschaften. Hier sind alle binären Baumtypen im Detail:

1. Vollständiger Binärbaum

Es ist eine spezielle Art eines binären Baums, der entweder null Kinder oder zwei Kinder hat. Dies bedeutet, dass alle Knoten in diesem Binärbaum entweder zwei untergeordnete Knoten seines übergeordneten Knotens haben sollten oder der übergeordnete Knoten selbst der Blattknoten oder der externe Knoten ist.

Mit anderen Worten, ein vollständiger Binärbaum ist ein eindeutiger Binärbaum, bei dem jeder Knoten außer dem externen Knoten zwei Kinder hat. Wenn es ein einzelnes Kind enthält, ist ein solcher Binärbaum kein vollständiger Binärbaum. Hier ist die Anzahl der Blattknoten gleich der Anzahl der internen Knoten plus eins. Die Gleichung lautet wie folgt: L=I+1, wobei L die Anzahl der Blattknoten und I die Anzahl der internen Knoten ist.

Hier ist die Struktur eines vollständigen Binärbaums:

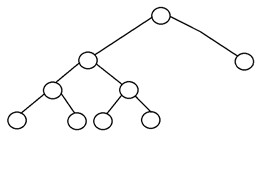
2. Vollständiger Binärbaum

Ein vollständiger Binärbaum ist ein weiterer spezifischer Typ eines Binärbaums, bei dem alle Baumebenen vollständig mit Knoten gefüllt sind, mit Ausnahme der untersten Ebene des Baums. Auch in der letzten oder untersten Ebene dieses Binärbaums sollte sich jeder Knoten möglicherweise auf der linken Seite befinden. Hier ist die Struktur eines vollständigen Binärbaums:

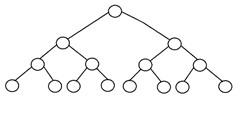
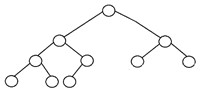
3. Perfekter binärer Baum

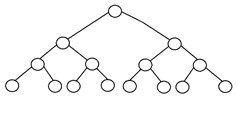
Ein binärer Baum wird als "perfekt" bezeichnet, wenn alle internen Knoten streng zwei Kinder haben und sich jeder externe oder Blattknoten auf derselben Ebene oder in derselben Tiefe innerhalb eines Baums befindet. Ein perfekter binärer Baum mit der Höhe „h“ hat 2h – 1 Knoten. Hier ist die Struktur eines perfekten Binärbaums:

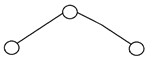
4. Ausgewogener Binärbaum

Ein binärer Baum wird als „ausgeglichen“ bezeichnet, wenn die Baumhöhe O(logN) ist, wobei „N“ die Anzahl der Knoten ist. In einem ausgeglichenen Binärbaum sollte die Höhe des linken und des rechten Teilbaums jedes Knotens höchstens um eins variieren. Ein AVL-Baum und ein Rot-Schwarz-Baum sind einige gängige Beispiele für Datenstrukturen, die einen ausgewogenen binären Suchbaum erzeugen können. Hier ist ein Beispiel für einen ausgeglichenen Binärbaum:

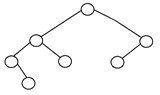
5. Degenerierter Binärbaum

Ein Binärbaum wird als degenerierter Binärbaum oder pathologischer Binärbaum bezeichnet, wenn jeder interne Knoten nur ein einziges Kind hat. Solche Bäume ähneln in Bezug auf die Leistung einer verknüpften Liste. Hier ist ein Beispiel für einen degenerierten Binärbaum:

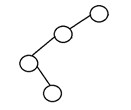
Vorteile eines binären Baums

• Die Suchoperation in einem Binärbaum ist im Vergleich zu anderen Bäumen schneller
• Nur zwei Durchläufe reichen aus, um die Elemente in sortierter Reihenfolge bereitzustellen
• Es ist einfach, die maximalen und minimalen Elemente aufzunehmen
• Beim Traversieren von Graphen werden auch binäre Bäume verwendet
• Das Konvertieren verschiedener Postfix- und Präfixausdrücke ist mithilfe von Binärbäumen möglich

Lesen Sie auch: Entscheidungsbäume beim maschinellen Lernen: Funktionen, Klassifizierung, Vor- und Nachteile

Fazit

Der Binärbaum ist einer der am häufigsten verwendeten Bäume in der Datenstruktur. Jeder der binären Baumtypen hat seine einzigartigen Merkmale. An diese Datenstrukturen werden in der angewandten Informatik besondere Anforderungen gestellt. Wir hoffen, dass dieser Artikel über Arten von Binärbäumen hilfreich war. upGrad bietet verschiedene Kurse in Data Science, Machine Learning, Big Data und mehr an.

Wenn Sie neugierig sind, etwas über Data Science zu lernen, schauen Sie sich das Executive PG Program in Data Science von IIIT-B & upGrad an, das für Berufstätige entwickelt wurde und mehr als 10 Fallstudien und Projekte, praktische Workshops, Mentoring mit Branchenexperten, 1 -on-1 mit Branchenmentoren, mehr als 400 Stunden Lern- und Jobunterstützung bei Top-Unternehmen.