5种二叉树解释[附插图]

在计算机科学中，各种数据结构有助于以不同形式排列数据。 其中，树是一种广泛使用的抽象数据结构，它模拟了层次树结构。 树通常具有根值和由其父节点的子节点形成的子树。 树是非线性数据结构。

一般的树数据结构对它可以容纳的子节点的数量没有限制。 然而，这不是二叉树的情况。 本文将学习一种特定的树数据结构——二叉树和二叉树的类型。

什么是二叉树数据结构？

二叉树是一种树型非线性数据结构，每个父级最多有两个子级。 二叉树中的每个节点都有一个左右引用以及数据元素。 树的层次结构顶部的节点称为根节点。 拥有其他子节点的节点是父节点。

一个父节点有两个子节点：左子节点和右子节点。 散列、网络流量路由数据、数据压缩、准备二叉堆和二叉搜索树是使用二叉树的一些应用程序。

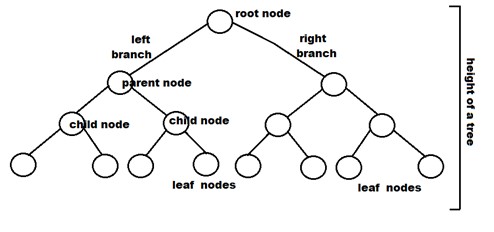
与二叉树和二叉树类型相关的术语

• 节点：它代表树中的一个终止点。
• 根：树的最顶层节点。
• 父节点：树中的每个节点（除了根节点）至少有一个自己的子节点，称为父节点。
• 子节点：当远离根节点时直接来自父节点的节点是子节点。
• 叶节点：这些是外部节点。 它们是没有子节点的节点。
• 内部节点：顾名思义，这些是具有至少一个孩子的内部节点。
• 树的深度：从树的节点到根的边数。
• 树的高度：它是从节点到最深叶子的边数。 树高也被认为是根高度。

现在您已经熟悉了与二叉树和二叉树类型相关的术语，是时候了解二叉树组件了。 查看我们的数据科学课程，深入了解二进制结构和组件。

二叉树组件

有三个二叉树组件。 每个二叉树节点都有这三个与之关联的组件。 理解这三个二叉树组件成为程序员的基本概念：

1. 数据元素
2. 指向左子树的指针
3. 指向右子树的指针

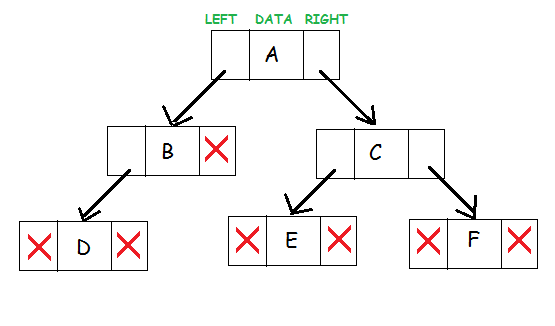
资源

这三个二叉树组件代表一个节点。 数据位于中间。 左指针指向子节点，形成左子树。 右指针指向其右边的子节点，创建右子树。

阅读：数据科学的热门猜测问题和信息方法

二叉树的类型

二叉树有多种类型，每种二叉树类型都有其独特的特征。 以下是每种二叉树类型的详细信息：

1. 全二叉树

它是一种特殊的二叉树，有零个孩子或两个孩子。 这意味着该二叉树中的所有节点都应该具有其父节点的两个子节点，或者父节点本身就是叶节点或外部节点。

换句话说，完整二叉树是唯一的二叉树，其中除了外部节点之外的每个节点都有两个孩子。 当它只有一个孩子时，这样的二叉树将不是完整的二叉树。 这里，叶子节点的数量等于内部节点的数量加一。 这个方程就像L=I+1，其中 L 是叶节点的数量，I 是内部节点的数量。

下面是完整二叉树的结构：

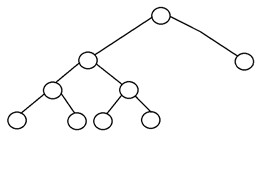
2. 完全二叉树

完全二叉树是另一种特定类型的二叉树，其中除了树的最低层之外，所有树层都完全用节点填充。 此外，在这棵二叉树的最后一层或最低层中，每个节点都可能位于左侧。 完整二叉树的结构如下：

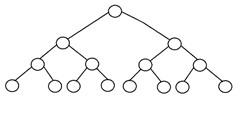
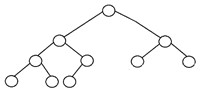
3. 完美二叉树

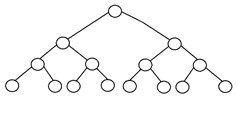
如果所有内部节点都有严格的两个子节点，并且每个外部节点或叶节点在树中处于相同级别或相同深度，则称二叉树是“完美的”。 高度为“h”的完美二叉树有 2h – 1 个节点。 下面是完美二叉树的结构：

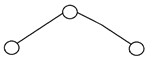
4.平衡二叉树

如果树高为 O(logN)，则称二叉树是“平衡的”，其中“N”是节点数。 在平衡二叉树中，每个节点的左右子树的高度最多相差一个。 AVL 树和红黑树是可以生成平衡二叉搜索树的数据结构的一些常见示例。 下面是一个平衡二叉树的例子：

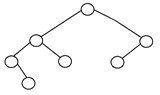
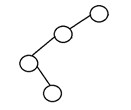
5. 退化二叉树

如果每个内部节点只有一个子节点，则称二叉树为退化二叉树或病态二叉树。 这样的树在性能方面类似于链表。 下面是一个退化二叉树的例子：

二叉树的好处

• 与其他树相比，二叉树中的搜索操作更快
• 只需两次遍历就足以按排序顺序提供元素
• 很容易拿起最大和最小的元素
• 图遍历也使用二叉树
• 使用二叉树可以转换不同的后缀和前缀表达式

另请阅读：机器学习中的决策树：功能、分类、优缺点

结论

二叉树是数据结构中使用最广泛的树之一。 每种二叉树类型都有其独特的特征。 这些数据结构在应用计算机科学中有特定的要求。 我们希望这篇关于二叉树类型的文章对您有所帮助。 upGrad 提供数据科学、机器学习、大数据等方面的各种课程。

如果您想了解数据科学，请查看 IIIT-B 和 upGrad 的数据科学执行 PG 计划，该计划是为在职专业人士创建的，提供 10 多个案例研究和项目、实用的实践研讨会、行业专家的指导、1与行业导师一对一，400 多个小时的学习和顶级公司的工作协助。