5種類の二分木の説明[イラスト付き]

コンピュータサイエンスでは、さまざまなデータ構造がさまざまな形式のデータの配置に役立ちます。 その中で、ツリーは、階層的なツリー構造をシミュレートする、広く使用されている抽象データ構造です。 ツリーには通常、ルート値と、親ノードの子ノードによって形成されるサブツリーがあります。 ツリーは非線形のデータ構造です。

一般的なツリーデータ構造には、保持できる子ノードの数に制限はありません。 しかし、これは二分木には当てはまりません。 この記事では、特定のツリーデータ構造（二分木と二分木の種類）について学習します。

二分木データ構造とは何ですか？

二分木は、親ごとに最大2つの子を持つツリータイプの非線形データ構造です。 二分木のすべてのノードには、データ要素とともに左右の参照があります。 ツリーの階層の最上位にあるノードは、ルートノードと呼ばれます。 他のサブノードを保持するノードは親ノードです。

親ノードには、左の子と右の子の2つの子ノードがあります。 ハッシュ、ネットワークトラフィック用のデータのルーティング、データ圧縮、バイナリヒープの準備、およびバイナリ検索ツリーは、バイナリツリーを使用するアプリケーションの一部です。

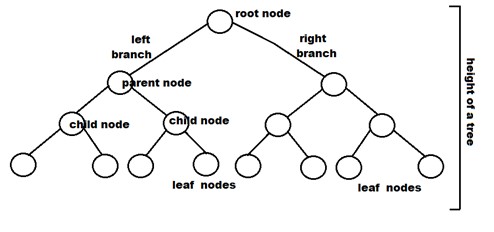
二分木に関連する用語と二分木の種類

• ノード：ツリー内の終点を表します。
• ルート：ツリーの最上位ノード。
• 親：独自のサブノードが少なくとも1つあるツリー内の各ノード（ルートを除く）は、親ノードと呼ばれます。
• 子：ルートから離れるときに親ノードからまっすぐに来たノードが子ノードです。
• リーフノード：これらは外部ノードです。 それらは子を持たないノードです。
• 内部ノード：名前が示すように、これらは少なくとも1つの子を持つ内部ノードです。
• ツリーの深さ：ツリーのノードからルートまでのエッジの数はです。
• 木の高さ：ノードから最も深い葉までのエッジの数です。 木の高さもルートの高さと見なされます。

二分木に関連する用語と二分木の種類に精通しているので、二分木の構成要素を理解する時が来ました。 データサイエンスコースをチェックして、バイナリ構造とコンポーネントについて詳しく学んでください。

二分木コンポーネント

3つのバイナリツリーコンポーネントがあります。 すべての二分木ノードには、これら3つのコンポーネントが関連付けられています。 プログラマーにとって、これら3つのバイナリツリーコンポーネントを理解することは不可欠な概念になります。

1. データ要素
2. 左サブツリーへのポインタ
3. 右サブツリーへのポインタ

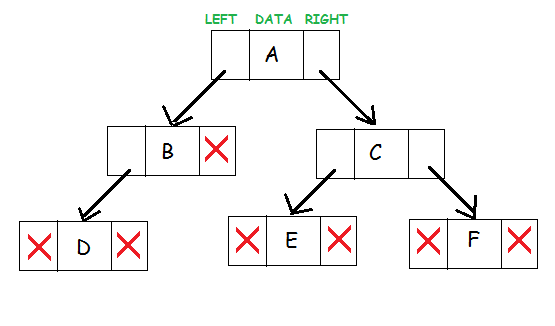
ソース

これらの3つの二分木コンポーネントはノードを表します。 データは中央にあります。 左側のポインタは子ノードを指し、左側のサブツリーを形成します。 右のポインタはその右の子ノードを指し、右のサブツリーを作成します。

読む：データサイエンスのための上位の推測の質問と有益な方法

二分木の種類

二分木にはさまざまな種類があり、それぞれに固有の特徴があります。 それぞれの二分木タイプの詳細は次のとおりです。

1.完全な二分木

これは、子が0個または子が2個ある特殊な種類の二分木です。 つまり、そのバイナリツリー内のすべてのノードには、親ノードの2つの子ノードがあるか、親ノード自体がリーフノードまたは外部ノードである必要があります。

つまり、完全な二分木は、外部ノードを除くすべてのノードに2つの子がある一意の二分木です。 子が1つしかない場合、そのような二分木は完全な二分木にはなりません。 ここで、リーフノードの数は内部ノードの数に1を加えたものに等しくなります。 方程式はL=I + 1のようなものです。ここで、Lはリーフノードの数、Iは内部ノードの数です。

完全な二分木の構造は次のとおりです。

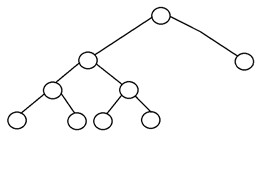
2.完全な二分木

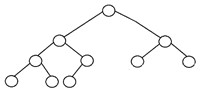
完全な二分木は、ツリーの最下位レベルを除いて、すべてのツリーレベルがノードで完全に満たされている別の特定のタイプの二分木です。 また、このバイナリツリーの最後または最下位レベルでは、すべてのノードが左側に存在する可能性があります。 完全な二分木の構造は次のとおりです。

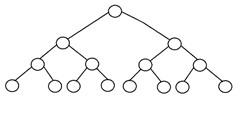
3.完璧な二分木

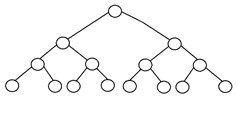
すべての内部ノードに厳密に2つの子があり、すべての外部ノードまたはリーフノードがツリー内で同じレベルまたは同じ深さにある場合、バイナリツリーは「完全」であると言われます。 高さが「h」の完全な二分木には、2h –1ノードがあります。 完全な二分木の構造は次のとおりです。

4.平衡二分木

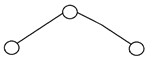
ツリーの高さがO（logN）の場合、バイナリツリーは「バランスが取れている」と言われます。ここで、「N」はノードの数です。 平衡二分木では、各ノードの左右のサブツリーの高さは最大で1つ異なる必要があります。 AVLツリーと赤黒木は、平衡二分探索木を生成できるデータ構造の一般的な例です。 平衡二分木の例を次に示します。

5.二分木を縮退させる

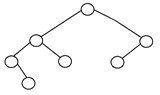
すべての内部ノードに子が1つしかない場合、バイナリツリーは縮退したバイナリツリーまたは病理学的なバイナリツリーと呼ばれます。 このようなツリーは、パフォーマンスの点でリンクリストに似ています。 縮退した二分木の例を次に示します。

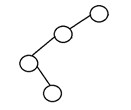
二分木の利点

• 二分木の検索操作は、他のツリーと比較して高速です
• ソートされた順序で要素を提供するには、2つのトラバーサルだけで十分です。
• 最大要素と最小要素を簡単に取得できます
• グラフ走査も二分木を使用します
• 二分木を使用して、さまざまな接尾辞と接頭辞の式を変換できます

また読む：機械学習の決定木：機能、分類、長所と短所

結論

二分木は、データ構造で最も広く使用されているツリーの1つです。 それぞれの二分木タイプには、独自の機能があります。 これらのデータ構造には、応用コンピュータサイエンスにおける特定の要件があります。 二分木の種類に関するこの記事がお役に立てば幸いです。 upGradは、データサイエンス、機械学習、ビッグデータなどのさまざまなコースを提供しています。

データサイエンスについて知りたい場合は、IIIT-B＆upGradのデータサイエンスのエグゼクティブPGプログラムをチェックしてください。これは、働く専門家向けに作成され、10以上のケーススタディとプロジェクト、実践的なハンズオンワークショップ、業界の専門家とのメンターシップを提供します。1業界のメンターとの1対1、400時間以上の学習、トップ企業との仕事の支援。