Spiegazione di 5 tipi di albero binario [con illustrazioni]

In informatica, varie strutture di dati aiutano a organizzare i dati in forme diverse. Tra questi, gli alberi sono strutture dati astratte ampiamente utilizzate che simulano una struttura ad albero gerarchica. Un albero di solito ha un valore radice e sottoalberi formati dai nodi figlio dai suoi nodi padre. Gli alberi sono strutture dati non lineari.

Una struttura dati ad albero generale non ha limiti al numero di nodi figli che può contenere. Tuttavia, questo non è il caso di un albero binario. Questo articolo imparerà a conoscere una struttura di dati ad albero specifica: albero binario e tipi di albero binario .

Che cos'è la struttura dei dati ad albero binario?

Un albero binario è una struttura di dati non lineare di tipo albero con un massimo di due figli per ciascun genitore. Ogni nodo in un albero binario ha un riferimento sinistro e destro insieme all'elemento dati. Il nodo in cima alla gerarchia di un albero è chiamato nodo radice. I nodi che contengono altri sottonodi sono i nodi principali.

Un nodo padre ha due nodi figlio: il figlio sinistro e il figlio destro. Hashing, instradamento dei dati per il traffico di rete, compressione dei dati, preparazione di heap binari e alberi di ricerca binari sono alcune delle applicazioni che utilizzano un albero binario.

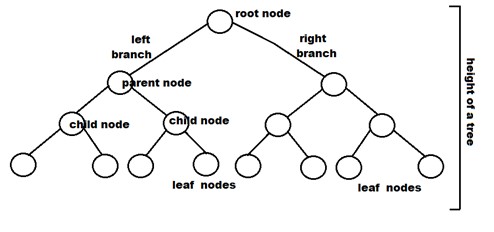
Terminologie associate agli alberi binari e tipi di alberi binari

• Nodo: rappresenta un punto terminale in un albero.
• Radice: il nodo più in alto di un albero.
• Genitore: ogni nodo (a parte la radice) in un albero che ha almeno un proprio sottonodo è chiamato nodo padre.
• Figlio: un nodo che proviene direttamente da un nodo padre quando ci si allontana dalla radice è il nodo figlio.
• Nodo foglia: sono nodi esterni. Sono i nodi che non hanno figli.
• Nodo interno: come suggerisce il nome, si tratta di nodi interni con almeno un figlio.
• Profondità di un albero: il numero di spigoli dal nodo dell'albero alla radice è.
• Altezza di un albero: è il numero di spigoli dal nodo alla foglia più profonda. L'altezza dell'albero è anche considerata l'altezza della radice.

Poiché ora hai familiarità con le terminologie associate all'albero binario e i tipi di albero binario, è tempo di comprendere i componenti dell'albero binario . Dai un'occhiata ai nostri corsi di scienza dei dati per conoscere in modo approfondito la struttura e i componenti binari.

Componenti dell'albero binario

Ci sono tre componenti dell'albero binario . Ogni nodo dell'albero binario ha questi tre componenti associati. Diventa un concetto essenziale per i programmatori comprendere questi tre componenti dell'albero binario:

1. Elemento dati
2. Puntatore al sottoalbero sinistro
3. Puntatore al sottoalbero destro

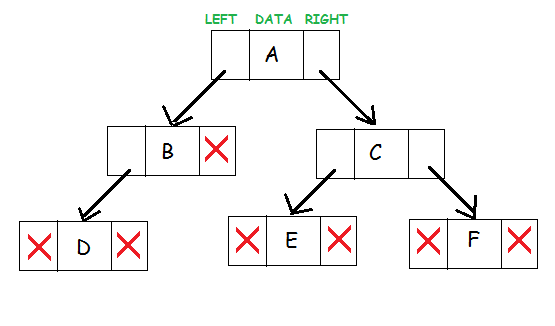
Fonte

Questi tre componenti dell'albero binario rappresentano un nodo. I dati risiedono nel mezzo. Il puntatore sinistro punta al nodo figlio, formando il sottoalbero sinistro. Il puntatore destro punta al nodo figlio alla sua destra, creando il sottoalbero giusto.

Leggi: Principali domande di stima e metodi informativi per la scienza dei dati

Tipi di alberi binari

Esistono vari tipi di alberi binari e ciascuno di questi tipi di alberi binari ha caratteristiche uniche. Ecco ciascuno dei tipi di albero binario in dettaglio:

1. Albero binario completo

È un tipo speciale di albero binario che ha zero figli o due figli. Significa che tutti i nodi in quell'albero binario dovrebbero avere due nodi figli del suo nodo genitore o il nodo genitore è esso stesso il nodo foglia o il nodo esterno.

In altre parole, un albero binario completo è un albero binario univoco in cui ogni nodo tranne il nodo esterno ha due figli. Quando contiene un singolo figlio, un tale albero binario non sarà un albero binario completo. Qui la quantità di nodi foglia è uguale al numero di nodi interni più uno. L'equazione è come L=I+1, dove L è il numero di nodi foglia e I è il numero di nodi interni.

Ecco la struttura di un albero binario completo:

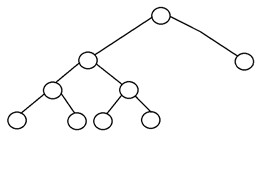
2. Completa l'albero binario

Un albero binario completo è un altro tipo specifico di albero binario in cui tutti i livelli dell'albero sono riempiti interamente di nodi, tranne il livello più basso dell'albero. Inoltre, nell'ultimo o nel livello più basso di questo albero binario, ogni nodo dovrebbe risiedere possibilmente sul lato sinistro. Ecco la struttura di un albero binario completo:

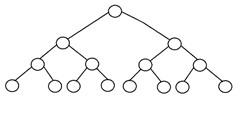
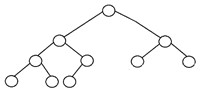
3. Albero binario perfetto

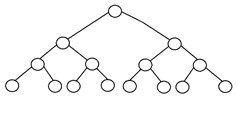
Un albero binario si dice "perfetto" se tutti i nodi interni hanno rigorosamente due figli e ogni nodo esterno o foglia si trova allo stesso livello o alla stessa profondità all'interno di un albero. Un albero binario perfetto con altezza 'h' ha 2h – 1 nodo. Ecco la struttura di un perfetto albero binario:

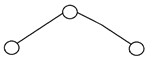
4. Albero binario bilanciato

Un albero binario si dice 'bilanciato' se l'altezza dell'albero è O(logN), dove 'N' è il numero di nodi. In un albero binario bilanciato, l'altezza dei sottoalberi sinistro e destro di ciascun nodo dovrebbe variare al massimo di uno. Un albero AVL e un albero rosso-nero sono alcuni esempi comuni di struttura dati in grado di generare un albero di ricerca binario bilanciato. Ecco un esempio di albero binario bilanciato:

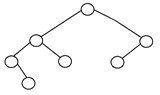
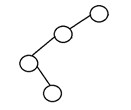
5. Albero binario degenerato

Si dice che un albero binario sia un albero binario degenerato o un albero binario patologico se ogni nodo interno ha un solo figlio. Tali alberi sono simili a un elenco collegato in termini di prestazioni. Ecco un esempio di albero binario degenere:

Vantaggi di un albero binario

• L'operazione di ricerca in un albero binario è più veloce rispetto ad altri alberi
• Sono sufficienti solo due attraversamenti per fornire gli elementi in ordine
• È facile raccogliere gli elementi massimi e minimi
• L'attraversamento del grafico utilizza anche alberi binari
• È possibile convertire diverse espressioni suffisso e prefisso utilizzando alberi binari

Leggi anche: Alberi decisionali nell'apprendimento automatico: funzioni, classificazione, pro e contro

Conclusione

L'albero binario è uno degli alberi più utilizzati nella struttura dei dati. Ciascuno dei tipi di albero binario ha le sue caratteristiche uniche. Queste strutture di dati hanno requisiti specifici nell'informatica applicata. Ci auguriamo che questo articolo sui tipi di alberi binari sia stato utile. upGrad offre vari corsi in data science, machine learning, big data e altro ancora.

Se sei curioso di conoscere la scienza dei dati, dai un'occhiata al programma Executive PG in Data Science di IIIT-B e upGrad, creato per i professionisti che lavorano e offre oltre 10 casi di studio e progetti, workshop pratici pratici, tutoraggio con esperti del settore, 1 -on-1 con mentori del settore, oltre 400 ore di apprendimento e assistenza al lavoro con le migliori aziende.